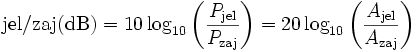Információátvitel és digitalizálás
analóg, folytonos jelek
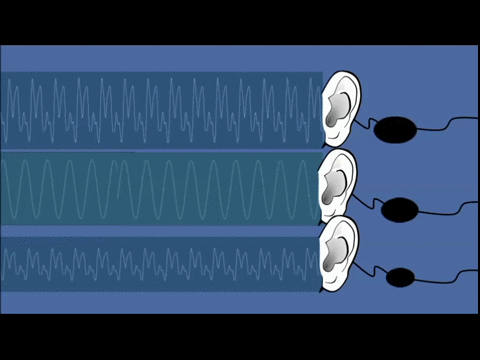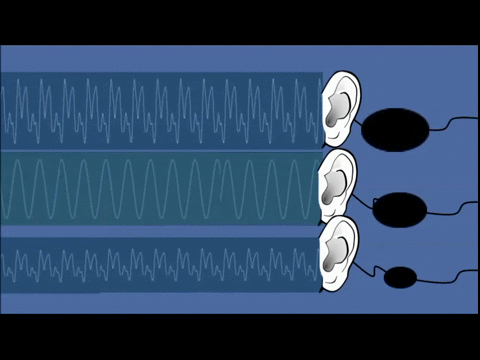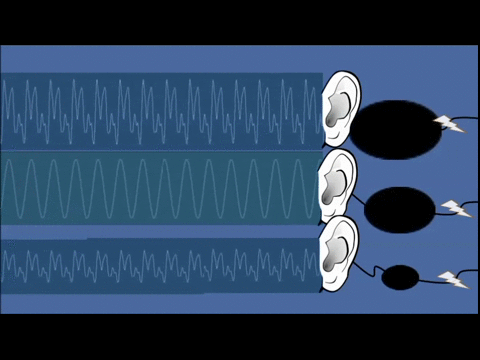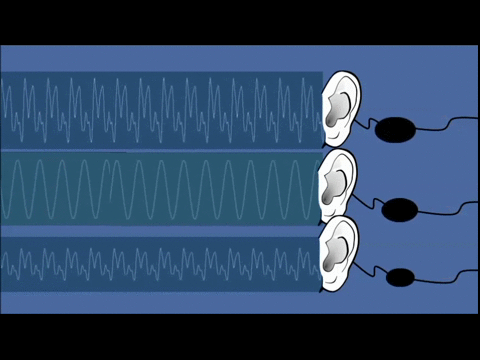
példa: hanghullám érzékelése (a hanghullám a levegő nyomásának periodikus változása a hang terjedésének irányában; a hanghullám longitudinális hullám)
- a hangjel nagysága térben és időben folytonosan változik (a hangjel amplitúdója az idő folytonos függvénye: A=A(t), ahol t∈[t1,t2])
- az emberi fül a kb. 20 Hz és 20 kHz közötti frekvenciájú hangrezgéseket képes érzékelni (vö. az egyvonalas a' hang frekvenciája 440Hz; egy oktáv hangköz pedig kétszeres frekvenciát jelent)
- a beszédhangok frekvenciája nagyobbrészt a 3000-4000 Hz frekvenciatartományba esik
- az emberi fül a mélyebb hangokra kevésbé érzékeny, mint a magasabb hangokra⇒
(a fül a legérzékenyebb a 3kHz és 4kHz közötti frekvenciájú hangokra)
- a hangjel nagysága és intenzitása (erőssége, teljesítménye stb.) két szélső érték között tetszőleges lehet (pl. az amplitúdó esetén
A∈[A1,A2];
a hullám intenzitása esetén pedig P∈[P0,Pmax], ahol P∼A2)
(megjegyzés: a hanghullám intenzitását egyes esetekben más szimbólummal, pl. 'J'-vel jelölik)
- az emberi fül a hallásküszöb (P0) és a fájdalomküszöb (Pmax) közötti intenzitású hangrezgéseket képes érzékelni
- P0≃10−12 W/m2
- Pmax≃10−1 W/m2
-
egy adott frekvenciájú hang erősségét decibelben
E=10*log10(P/P0)
módon kaphatjuk meg
- a hangosság mértékegysége a phon (vagy magyarosan fon)
(1 kHz frekvenciájú hang és P0=10−12 W/m2 hallásküszöb mellett egy P≥P0 intenzitású hang hangosságát
H=10*log10(P/P0)
módon kaphatjuk meg 'phon' egységben)
- 1 kHz frekvenciájú hang esetén a hang decibelben kifejezett hangerőssége és phon-ban kifejezett hangossága megegyezik (E=H)
- egy adott frekvenciájú és erősségű hang hangosságát (azaz a hang fülünk által érzékelt erősségét) a Fletcher-Munson izophon görbék⇒ alapján kaphatjuk meg
A hanghullám amplitúdójának (vagy teljesítményének) nagyságát hangosságként, a hanghullám frekvenciáját pedig hangmagasságként érzékeljük.
példa: az emberi fül érzékenysége háttérzaj hiányában
- hallásküszöb: 0 phon
(P=P0 ⇒ P/P0=1, H=0)
- "alkalmazkodó" hallásküszöb: a hallásküszöb értéke megnő háttérzaj mellett
- suttogás: kb. 20 phon
(P=100*P0 ⇒ P/P0=100=102, H=20)
- óraketyegés: kb. 30 phon
(P=1000*P0 ⇒ P/P0=1000=103, H=30)
- "normális" hangerejű beszéd: kb. 50 phon
(P=105*P0 ⇒ P/P0=105, H=50)
- írógép: kb. 60 phon
- kiabálás: kb. 80 phon
- motorkerékpár: kb. 100 phon
(P=1010*P0 ⇒ P/P0=1010, H=100)
- fájdalomküszöb: kb. 130 phon
Megjegyzések:
(1) Az emberi fül érzékenysége függ a hang frekvenciájától.⇒
(2) Az emberi fül esetében a hangosság 10 phon mértékű növekedését érzékeljük közelítőleg kétszer olyan erős hangnak (tehát pl. az írógép hangját kétszer olyan hangosnak érzékeljük, mint a normális beszédet).
digitális, diszkrét jelek
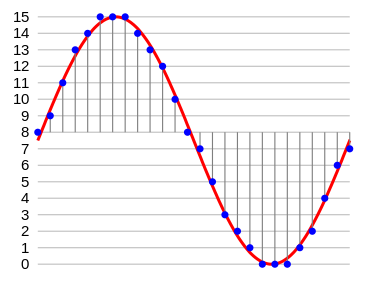

a digitalizálás során az információt hordozó analóg, folytonos jelek jellemző értékeit diszkrét jelek, rendszerint számok segítségével adjuk meg (vö. digit = számjegy)
- a jeleket leíró számokat, ill. számsorozatokat a legtöbbször adott számú biten, kettes számrendszerben ábrázoljuk
példa: hanghullám digitalizálása (ún. impulzuskód-moduláció, PCM)
- a diszkrét jelek időtartama egy meghatározott (rendszerint rövid) érték (mintavétel; ún. időbeli kvantálás)
- audio CD-k: egy másodperc alatt 44100 mintavétel történik (f=44.1 kHz, ∆t≅0,0227 ms)
- a diszkrét jelek nagysága csak néhány, előre meghatározott érték lehet (jelnagyság kvantálása)
- bináris jelek, 1 bites kódolás: 21=2 lehetséges érték (0, ill. 1)
- 3 bites kódolás: 23=8 lehetséges érték (0,1,2,...,7)
(ld. 2. ábra, 'y' tengely:
 )
)
(megjegyzés: a 2. ábra nem pontos, 3 bites kódolás esetén a 8-as érték már nem jelenhet meg)
- 4 bites kódolás: 24=16 lehetséges érték (0,1,2,...,15)
(ld. 1. ábra, 'y' tengely:
 )
)
- 8 bites kódolás: 28=256 lehetséges érték
- 16 bites kódolás, például audio CD-k: 216 = 65536 lehetséges érték
- ...
másik példa: zene megadása (leírása) kották segítségével
A hangjegyek elhelyezkedése a kottavonalak között a kottában ábrázolt zenei hangok magasságát adja meg.
A kulcs a kottavonalakhoz rendelt hangmagasságot adja meg (pl. violinkulcs vagy G kulcs esetén az alulról számított második kottavonalhoz rendeljük az egyvonalas g' hangot).
- néhány oktáv; egy oktávon belül 12 hang
- egy zenei hang magasságát a hanghullám frekvenciája adja meg
- egy oktáv hangköz kétszeres frekvenciának felel meg
- egyvonalas a' hang (ún. kamarahang): 440 Hz
- kétvonalas a'' hang: 880 Hz
- ...
jel/zaj viszony
Legyen adott
- az átvitt jel erőssége vagy nagysága: a jel teljesítménye, ill. intenzitása (Pjel) vagy a jel amplitúdója
(Ajel, ahol Pjel∼Ajel2)
- a zaj erőssége vagy nagysága: a zavaró jel teljesítménye, ill. intenzitása (Pzaj) vagy a jel amplitúdója
(Azaj, ahol Pzaj∼Azaj2)
Ekkor a jel-zaj viszony:

A jel-zaj viszony erősségét decibelben fejezzük ki:
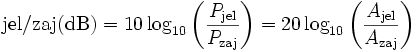
Például a hangerősséget a Pzaj=P0 választással kapjuk (ahol
P0=10−12 W/m2
a hallásküszöbhöz tartozó jel teljesítménye vagy intenzitása; itt nyilván
Pjel≥Pzaj teljesül).
A jel/zaj viszony esetében a teljesítmény tízszeres növekedésének 10 dB növekedés felel meg.
Egy üzenet információtartalmának kiszámítása
A matematikai információelmélet abból indul ki, hogy az információ bizonyos fokú tájékozatlanságot (bizonytalanságot, véletlenszerűséget, rendezetlenséget, "entrópiát" stb.) szüntet meg; egy üzenet átvételekor éppen annyi információt nyerünk, amennyi bizonytalanság megszűnik (vö. Puskás-Szendrei-Szerényi 1967: 107; Könyves Tóth 1982: 15).
Egy üzenetbe foglalt információt a benne kifejezett esemény ("az ... esemény bekövetkezett") előre nem látható jellegével lehet kiszámítani, ill. mérni.
Tegyük fel, hogy üzenetet, "hírt" kaptunk arról, hogy egy E esemény bekövetkezett. Az üzenet információtartalma:
| I [a kapott információ arról, hogy egy E esemény bekövetkezett]
| = log2
| {
|
P1 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele után]
P2 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt]
| }
|
Kettes logaritmust használva az információtartalom mértékegysége a már korábban bevezetett bit lesz.
Az üzenet bitben kifejezett információtartalma megadja, hogy pl. barkochba játékkal optimális esetben (azaz "ügyesen" kérdezve) hány kérdést kellene feltennünk, ha meg akarjuk tudni, hogy az
Ω = {E1, E2, ..., En}
eseménytér melyik eseménye következett be.
Ha a kapott információ pontos és hiteles, az üzenet címzettje biztos lehet abban, hogy az az esemény, amelynek a bekövetkezését az üzenet hírül adta, valóban bekövetkezett (azaz az E esemény bekövetkezésének valószínűsége az üzenet átvétele után P1=1).
Ekkor a fenti képlet leegyszerűsödik:
| I [a kapott információ arról, hogy egy E esemény bekövetkezett]
| = log2
| {
|
1
P2 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt]
| }
|
Ezt átalakítva a következő egyszerű képletet kapjuk:
I = log2(1/P)= − log2(P)
ahol P=P2 az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt.
(Példa: egy pénzfeldobás vagy egy kockadobás eredménye mennyi információt jelent?⇒)
A valószínűség klasszikus kiszámítási módja:
a "kedvező" elemi események száma (k) elosztva az összes elemi esemény számával (n). Képletben kifejezve:
P = k/n
Jegyezzük meg, hogy a fenti képlet csak akkor alkalmazható, ha minden elemi esemény egyenlően valószínű. (Ilyenkor ún. klasszikus valószínűségi eloszlásról beszélünk.)
Információátvitel és digitalizálás
Az információátvitel alapmodellje
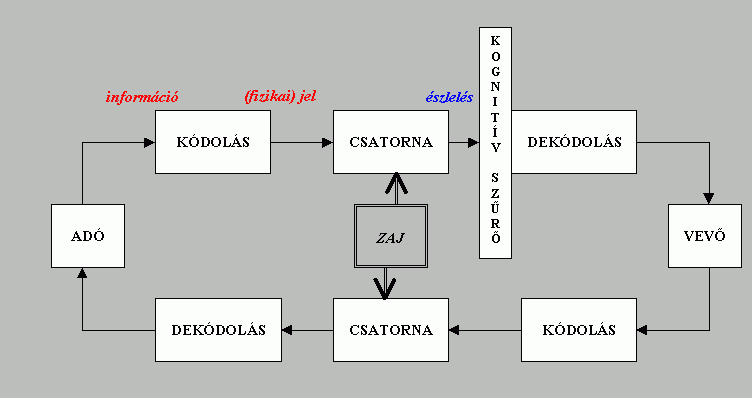
A modell elemei (lényegében Shannon és Weaver kommunikációs modellje szerint):
- adó oldal
- adó, információforrás
- az információ megadása; üzenet kialakítása
- információ kódoló; az információ kódolása
- jeladó; a kódolt információ fizikai jelekké alakítása
- átviteli csatorna
- fizikai jel átvitele (pl. hangrezgések formájában)
- zajforrás, zavaró jelek (pl. háttérzaj)
- vevő oldal
- jelérzékelő; a fizikai jelek visszaalakítása kódokká
- információ dekódoló; a kódolt információ visszanyerése
- zajszűrés; hibafelismerés és hibajavítás
- kognitív szűrő (szelektív figyelem, szelektív torzítás, szelektív emlékezet)
- vevő, "információnyelő"
- az információ feldolgozása
- az információ tárolása
- az információ felhasználása
- ...
A zajforrás például időben állandó (rendszeres vagy "véletlen") zajt eredményezhet, amelyet a jel/zaj viszonnyal jellemezhetünk. A zaj az átvitel hibáit eredményezheti, de redundáns ("felesleges", elhagyható, az átvitt információ szempontjából nem használt jeleket is tartalmazó) jelátvitel esetén elvileg lehetséges hibafelismerő és/vagy hibajavító kódok használata.
Hibafelismerő kódok alkalmazása esetén a vevő kérheti az adótól a hibás információ újraküldését.
Hibajavító kódok alkalmazása esetén a vevőnek lehetősége van bizonyos mértékű átviteli hiba kijavítására.
Shannon és Weaver modellje szerint a kommunikáció lényege az információk továbbítása és feldolgozása. A modellt eredetileg a modern telekommunikációs eszközök egyes sajátságainak matematikai leírására (csatorna kapacitása, redundancia, kódok használata, titkosítás stb.) fejlesztették ki, később azonban általánosították, és ma már széles körben használják, lényegében bármilyen kommunikációs folyamat modellezésére (Buda 2001: 36, Griffin 2001: 36-38).
Az emberi, társas kommunikáció egyes eseteiben (például reklámkommunikáció, tanár-diák kommunikáció stb.) célszerű kiegészíteni a modellt egy ún. kognitív szűrővel, amelynek hatása például a
szelektív figyelem,
szelektív torzítás és
szelektív emlékezet
jelenségeiben figyelhető meg.
további információk:
Shannon és Weaver információelméleti (híradástechnikai) modellje (2020-03-03)
Redundancia (2020-03-03)
Hibajavítás (2020-03-03)
Paritásbit (2020-03-03)
analóg és digitális jelek
A fizikai jelek lehetnek
- analóg jelek és
- digitális jelek.
Az analóg jelek térben és időben folytonosak: egy (folytonos) intervallumból vesszük a jelkészlet értékeit, és ezek (folytonos) sorozatát használjuk az információk megadására. A folytonosság miatt mind a jelkészlet, mind a továbbított jelsorozat elvileg végtelen sok értéket tartalmaz.
- két szélső érték között a fizikai jel nagysága tetszőleges lehet
- a jel nagysága időben folytonosan változik (vagy változhat)
Példa: analóg hangjelek vagy hangrezgések (a levegő nyomásának periodikus változásai), amelyek megadhatóak az amplitúdó időbeli változását leíró folytonos függvénnyel: A=A(t), ahol t ∊ [t1, t2], A ∊ [A1, A2] (egy ilyen egyváltozós függvény legegyszerűbben egy kétdimenziós grafikonnal ábrázolható).

A digitális jelek térben és időben
diszkrétek, egy véges jelkészletet és ezekből összeállított jelsorozatot használnak az információk megadására. (A jelkészlet végessége miatt az egyes jelek mindig megadhatók számkódokkal, ezáltal pedig a jelsorozatok megadhatók számok sorozataként.)
- a fizikai jel nagysága csak néhány meghatározott érték lehet (pl. bináris jel esetén két lehetséges érték van, kották esetében néhány oktávot használunk, audio CD-k esetében a jelnagyság 216=65536 lehetséges értékét különböztetjük meg stb.)
- az egyes fizikai jelek időtartama egy meghatározott (rendszerint rövid) érték, amelyhez egy meghatározott jelnagyság tartozik
Példa: digitális hangok, amelyek szemléletesen pl. egy táblázatban adhatóak
meg; a táblázat első sora az időértékeket tartalmazza, második (ill. több csatorna esetében harmadik, negyedik stb.) sorában pedig az egyes időértékekhez tartozó amplitúdóértékek szerepelnek.
Az analóg jelek átalakítása digitális jelekké az ún. digitalizálás.
Ez történik meg például az emberi fül által hallható (kb. 20 Hz és 20 kHz közötti) hangrezgések digitalizálásakor. Ennek egy formája az ún. impulzuskód-moduláció (PCM). Például a "hagyományos" zenei CD-k (CD Audio) esetében
– a mintavétel frekvenciája 44.1 kHz (emiatt a mintavétel időtartama ∆t ≅ 0,0227 ms),
– a mintavétel során a mért amplitúdóértékeket mindkét (bal és jobb) csatornán egy 16 bites (egész) szám adja meg, azaz az ún. digitalizálási vagy kvantálási mélység 16 bit (amely egy 0-65535 közötti számtartománynak felel meg); az így tárolt amplitúdóérték a hangok relatív erősségét adja meg.
Az ábrán az amplitúdóértékek kvantálási mélysége 4 bit, amely egy 0-15 közötti (illetve a [-8,7] közötti) számtartománynak felel meg.

Példa: CD Audio esetében kiszámíthatjuk, egy perc alatt mennyi a lejátszott információ mennyisége. Mivel egy másodperc alatt 44100 amplitúdóértéket tárolunk 16 biten és két (bal és jobb) csatornát használunk
I = 2*44100*16*60 bit = 84672000 bit = 10584000 bájt ≅ 10336 KB ≈ 10 MB
Például mp3 kódolást használva ennek az információnak elegendő kb. 10-12-ed részét tárolni ahhoz, hogy elfogadható minőségű zenei állományt kapjunk.
további információk:
Hang (2020-03-04)
Sound (2018-02-23)
Pulse-code modulation (2018-02-23)
Digitális hangrögzítés, kvantálás | Sulinet Tudásbázis (2020-03-03)
Compact Disc Digital Audio (2018-02-23)
Zenei hang (2020-03-04)
Kamarahang (2020-03-04)
Kottaírás (2020-03-04)
jel/zaj viszony, hangosság
Az információátvitel alapmodellje szerint az átvitel során figyelembe kell vennünk az átviteli csatornán megjelenő zajt is. Mind az átvitt jel, mind a zaj erősségét jellemezhetjük a jel teljesítményével (P) vagy a jel amplitúdójával (A). Kiindulva abból, hogy a jel teljesítménye az amplitúdó négyzetével arányos,
a jel/zaj viszony képlete:

A képlet kifejezi, hogy minél nagyobb az információt hordozó ("hasznos") fizikai jel amplitúdója (A), ill. teljesítménye (P) a zajt okozó ("káros") fizikai jel amplitúdójához, ill. teljesítményéhez képest, az információ átvitele annál hatékonyabb. Mivel a gyakorlatban a zaj erőssége több nagyságrenddel is kisebb lehet, mint a hasznos jel erőssége, érdemes a jel/zaj viszony logaritmusát használni. Ilyenkor a jel/zaj viszony egysége az ún. decibel (dB):
A jel/zaj viszony logaritmikus képlete:
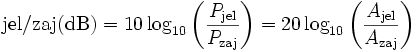
A logaritmus esetében
log(a*b) = log(a)+log(b)
és
log(an) = n*log(a)
teljesül.
Ezért például
– ha a hasznos jel amplitúdója tízszerese a zaj amplitúdójának
(Ajel=10*Azaj),
akkor a jel/zaj viszony értéke 20 dB;
– ha a hasznos jel amplitúdója százszorosa a zaj amplitúdójának
(Ajel=100*Azaj=102*Azaj),
akkor a jel/zaj viszony értéke
2 * 20 dB=40 dB,
– ha pedig a hasznos jel amplitúdója ezerszerese a zaj amplitúdójának
(Ajel=1000*Azaj=103*Azaj),
akkor a jel/zaj viszony értéke
3 * 20 dB=60 dB.
(Tízezerszeres szorzó esetén 80 dB, százezerszeres szorzó esetén 100 dB adódik stb.).
A jel/zaj viszony esetében az amplitúdóértékek közötti tízszeres szorzónak 20 dB növekedés felel meg.
Ugyanez a teljesítményértékek esetén 10 dB.
Ha a decibelt a hangerősség kifejezésére használják, amplitúdóértékek esetén dB SIL (Sound Intensity Level) mértékegységről, teljesítményértékek esetén dB SPL (Sound Power Level) mértékegységről beszélhetünk. Ilyenkor az ún. hallásküszöb (a még "éppen" hallható erősségű hang, dB SPL esetén P0 = 10-12 W/m2) erősségéhez képest adják meg a hang erősségét.
Érdemes megjegyezni, hogy dB SPL esetén, mivel log 2≈0,301029, a kétszeres szorzónak közelítőleg
10*log 2≈3 dB
felel meg, azaz 3 dB növekedés kétszer olyan erős (kétszer olyan "hangos") hangot jelent. (Ugyanez dB SIL esetén 6 dB.)
A továbbiakban dB SPL helyett egyszerűen dB-ről vagy decibelről beszélünk.
Az emberi fül különböző frekvenciájú hangokra különböző érzékenységű, ezért a decibel helyett az ún. phon mértékegységet használják az emberi fül által érzékelt (szubjektív) hangosság kifejezésére.
1 phon 1 kHz frekvenciájú hang erőssége decibelben megadva (összehasonlításképpen: a normál zenei 'A' hang frekvenciája 440 Hz, az egy oktávval magasabb 'A' hang esetében ez 880 Hz stb.).
Például
– a hallásküszöbnek megfelelő erősségű hang hangossága 0 phon,
– 20 phon kb. a suttogásnak,
– 30 phon kb. az óraketyegésnek,
– 50 phon kb. a "normális" hangerejű beszédnek,
– 60 phon kb. az írógép zajának,
– 80 phon kb. kiabálásnak,
– 100 phon kb. a motorkerékpár zajának,
– 130 phon pedig kb. a fájdalomküszöbnek felel meg.
A fenti értékek 1 kHz frekvenciájú hang esetén megegyeznek a hangerősség decibelben mért értékével. Érdemes megjegyezni, hogy mivel 10 dB növekedés a hangerősség tízszeres növekedésének felel meg, az emberi fül a hallásküszöbhöz tartozó hangerősség több, mint 1010-szeresét képes érzékelni.
Megjegyzés:
Az emberi fül esetében a hangosság 10 phon mértékű növekedését érzékeljük közelítőleg kétszer olyan erős hangnak. Vagyis a fül számára 3 phon növekedés (amely 1 kHz frekvenciájú hang esetén kétszeres hangerősséget jelent) még nem eredményez kétszer olyan erős hangot.
A hangosság jellemzésére ezért bevezették a son egységet.
1 son=40 phon, és ennél erősebb hangok esetén a hangosság 10 phon mértékű
növekedése
1 son növekedésnek felel meg (azaz pl. "normális" hangerejű beszéd esetén a hangosság 2 son=50 phon értékű).
Az ún. Fletcher-Munson izophon görbék a szubjektíven azonos hangosságúnak érzékelt hangerősséget (y tengely, pl. dB-ben megadva) ábrázolják a hangok frekvenciájának vagy magasságának (x tengely, Hz-ben megadva) függvényében:

Az emberi fül számára például 50 phon hangosságérzet eléréséhez
– 1 kHz esetében 50 dB,
– 5 kHz (magasabb hang) esetében kb. 40 dB,
– 100 Hz (mélyebb hang) esetén pedig kb. 60 dB
hangerősség szükséges ahhoz, hogy ugyanolyan erősségű hangot érzékeljünk.
Viszont pl. 30 Hz frekvencia (nagyon mély hang) esetén 10 decibelnél kevesebb (kb. 4-7 decibel) változás is elegendő 10 phon változás eléréséhez.
további információk:
Hang (2018-02-23)
A hallás (2018-02-23)
Jel-zaj viszony (2018-02-23)
Decibel (2018-02-23)
Hangosság (2018-02-23)
Sound Power, Intensity and Pressure (2018-02-23)
Zaj és rezgés, mint környezetszennyezés (2018-02-23)
egy üzenet információtartalmának kiszámítása
Korábban már szó volt róla, hogy az
információ gyakorlati (technikai) mennyisége az a digitális tárolókapacitás, amely szükséges az adott információ vagy adatmennyiség tárolásához.
Ezzel szemben egy üzenetbe foglalt információt a benne kifejezett esemény előre nem látható jellegével lehet kiszámítani, ill. mérni (Cullmann et al. 1973: 110).
Tegyük fel, hogy hírt kaptunk arról, hogy egy E esemény bekövetkezett. Az üzenet információtartalma képletben kifejezve:
| I [a kapott információ arról, hogy egy E esemény bekövetkezett]
| = log2
| {
|
P1 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele után]
P2 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt]
| }
|
Megjegyzés: a képlet akkor használható (ti. akkor ad nemnegatív értéket), ha
P1≥P2
teljesül.
Kettes logaritmust használva az információtartalom mértékegysége a már korábban bevezetett bit lesz.
Zaj nélküli, hibamentes átvitel és hiteles, "megbízható" adó esetén az üzenet címzettje biztos lehet abban, hogy az esemény valóban bekövetkezett (azaz a bekövetkezéséről kapott információ pontos és hiteles), azaz az E esemény bekövetkezésének valószínűsége az üzenet átvétele után P1 = 1. Ekkor a fenti képlet leegyszerűsödik:
| I [a kapott információ arról, hogy egy E esemény bekövetkezett]
| = log2
| {
|
1
P2 [az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt]
| }
|
Ezt átalakítva a következő egyszerű képletet kapjuk:
I = log2(1/P)= − log2(P)
,
ahol P = P2 az E esemény bekövetkezésének valószínűsége az üzenet átvétele előtt.
Például
- annak az eseménynek az információtartalma, hogy egy pénzérmét feldobva írást kaptunk, P = 0.5 = 1/2 miatt
I = log2(2) = 1 bit;
- annak az eseménynek az információtartalma pedig, hogy egy szabályos "hatos" kockát eldobva 4-et kaptunk, P = 1/6 miatt
I = log2(6) = 2,585 bit,
ezt felfelé kerekítve I ~ 3 bit adódik.
Ez azt jelenti, hogy ha pl. barkochba játékkal (csak eldöntendő, "igen-nem" típusú kérdéseket feltéve) kellett volna kitalálnunk a kockadobás eredményét, akkor legfeljebb három kérdést kellett volna feltennünk (de I < 3 miatt szerencsés esetben elég lehet akár két kérdés is).
A fenti példákban felhasználtuk a valószínűség "klasszikus" meghatározására vonatkozó képletet: ha egy kísérletnek 'n' számú különböző kimenetele lehetséges (azaz 'n' db "elemi" eseményünk van) és ezek azonos valószínűségűek, akkor egy elemi esemény valószínűsége 1/n. Ha pedig egy A "összetett" eseményt 'k' db elemi esemény alkot (azaz A akkor következik be, ha a 'k' db. elemi esemény valamelyike bekövetkezik), akkor az A összetett esemény valószínűsége P(A) = k/n.
A valószínűség klasszikus kiszámítási módja:
a "kedvező" elemi események száma elosztva az összes elemi esemény számával.
Például egy szabályos (nem "cinkelt") kocka esetében annak a valószínűsége, hogy párost dobunk Ppáros = 3/6 = 1/2, mivel páros számot háromféleképpen kaphatunk a kockadobással kapható hat számból.
további információk:
Bit (2018-02-23)
Hírérték (2018-02-23)
Valószínűségszámítás (2018-02-23)
Boda István, 2022.