Matematika 1 - Gyakorló feladatok

Az ekvivalenciareláció és a rendezési relációk

Gyakorló feladatok (vö. Veress 1996: 30-31):

Vizsgálja meg a következő relációk tulajdonságait! Állapítsa meg, melyek nevezetes relációk!

(a1) {(x,y) | x∈ℕ, y∈ℕ, x|y}

az oszthatóságot korábban úgy határoztuk meg,^⇒ hogy a természetes számok körében
    x|y ⇋ "van olyan q∈ℕ természetes szám, amelyre y=q*x teljesül"
Ennek megfelelően a feladatban megadott reláció tulajdonságai:
(1) reflexivitás: ha x∈ℕ tetszőleges természetes szám, akkor
x=1*x ⇒ x|x tehát (x,x) teljesül, vagyis a reláció reflexív;
(2.1) szimmetria: mivel pl. 3∣6 és 6∤3, vagyis a reláció nem szimmetrikus (egy ellenpélda elég!);
(2.2) aszimmetria: mivel a reláció reflexív, ezért nem lehet aszimmetrikus;^⇒
(2.3) antiszimmetria: legyenek x, y∈ℕ természetes számok és x≠y; feltéve, hogy
x|y ⇋ ∃q∈ℕ (y=q*x), három eset lehetséges ("esetszétválasztás"^⇒):
    (a) ha x=0 ∧ y=q*x ⇒ y=0 ⇒ x=y, ami x≠y miatt ellentmondás, vagyis ez az eset nem állhat fenn;
    (b) ha x>0 ∧ y=0 ⇒ y∤x (mivel a 0 egyedül önmagának az osztója);
    (c) ha x>0 ∧ y>0 ∧ y=q*x ⇒ q≥1, vagyis pozitív természetes számok esetén x|y ⇒ x≤y teljesül; ha feltesszük, hogy y|x, akkor x|y ∧ y|x ⇒ x≤y ∧ y≤x ⇒ x=y következik, amiből x≠y miatt ellentmondásra jutunk; ezért a feltétel nem lehet igaz, vagyis y∤x;
mivel az összes lehetséges esetben y∤x adódott, ezért x|y ∧ x≠y ⇒ y∤x teljesül, vagyis a reláció antiszimmetrikus;
(3) tranzitivitás: ha x, y, z∈ℕ olyan természetes számok, amelyekre x|y és y|z teljesül, akkor léteznek olyan p, q∈ℕ természetes számok, amelyekre y=p*x és z=q*y teljesül. Emiatt z=q*y=q*(p*x)=(q*p)*x teljesül, vagyis létezik olyan r=q*p természetes szám, amelyre z=r*x teljesül. Ez viszont azt jelenti, hogy x|z teljesül, vagyis a reláció tranzitív;
(4) trichotómia: mivel pl. 3∤7 és 7∤3, valamint nyilvánvalóan 3≠7, ezért a reláció nem trichotóm (egy ellenpélda itt is elég!).

(a2) {(x,y) | x∈ℕ⁺, y∈ℕ⁺, x|y}

(a3) {(x,y) | x∈ℕ⁺, y∈ℕ⁺, 1<x, 1<y, x|y}

(b) {(x,y) | x∈ℤ, y∈ℤ, x|y} (ℤ ⇆ "az egész számok halmaza")

(c) {(x,y) | x∈ℕ, y∈ℕ, 1<x, x≠y, x|y} (1<x<y, x|y ⇆ "az 'x' (természetes) szám valódi osztója az 'y' (természetes) számnak")

(d) {(x,y) | x∈ℕ, y∈ℕ, y=3*x}

(e) {(x,y) | x∈ℤ, y∈ℤ, x≡y (mod 4)} (x≡y (mod 4) ⇋ "az 'x' és 'y' (egész) számok 4-vel való osztási maradéka azonos")

Adott a következő osztályozás:
Η = { A₁, A₂, A₃ }, amelyre
    A₁={(2,3), (2,5), (2,9)}
    A₂={(4,7), (4,11)}
    A₃={(6,7)}
Adja meg azt az 'A' halmazt, amelyen az osztályozást értelmezzük, valamint azt a ψ ekvivalenciarelációt, amely ehhez az osztályozáshoz vezet!

Vizsgálja meg, hogy az adott 'A' halmaznak osztályozását jelentik-e a megadott {A₁, A₂, A₃} halmazrendszerek? Ha nem, változtassa meg a halmazrendszer elemeit! Adja meg az egyes osztályozásokhoz tartozó ψ ekvivalenciarelációt is!

(a) A = {ló, hal, egér, fecske, sas, sikló^⇒} és
A₁={hal, sikló}
A₂={fecske, sas}
A₃={ló, egér}

(b) A = {autó, repülőgép, busz, helikopter, hajó, kamion} és
A₁={autó, busz}
A₂={repülőgép, helikopter}
A₃={hajó}

Adjon meg egy ekvivalenciarelációt, amely létrehozza az 'A' halmazrendszer osztályozását! Végezze el és ábrázolja az 'A' halmaz osztályozását!
A = {{0, 2, 4, 6}, {0, 6}, {1, 2, 4, 8}, {1, 4}, {2, 4}}

Döntse el, hogy az alábbi Η halmazrendszerek osztályozásai-e a megadott 'A' halmaznak?

(a1) A=P∪Q (ahol P és Q tetszőleges halmazok)
Η = {P∖Q, P∩Q, Q∖P}

Vizsgáljuk meg, hogy Η elemei osztályoknak tekinthetőek-e.
(1) Η elemeinek uniója az A=P∪Q halmaz:
P∖Q ∪ P∩Q ∪ Q∖P = (P∩Q) ∪ (P∩Q) ∪ (Q∩P) = [(P∩Q) ∪ (P∩Q)] ∪ (Q∩P) = [P ∩ (Q ∪ Q)] ∪ (Q∩P) = [P ∩ I] ∪ (Q∩P) = P ∪ (Q∩P) = (P ∪ Q) ∩ (P ∪ P) = (P ∪ Q) ∩ I = (P ∪ Q) (megjegyzés: a pirossal aláhúzott átalakítás P kiemelése, ami a disztributív azonosság "megfordítása");
(2) Η elemei páronként diszjunktak:
(2.1) (P∖Q) ∩ (P∩Q) = (P∩Q) ∩ (P∩Q) = (P∩P) ∩ (Q∩Q) = P ∩ ∅ = ∅;
(2.2) (Q∖P) ∩ (P∩Q) = (Q∩P) ∩ (P∩Q) = (Q∩Q) ∩ (P∩P) = Q ∩ ∅ = ∅;
(2.3) (Q∖P) ∩ (P∖Q) = (Q∩P) ∩ (P∩Q) = (Q∩Q) ∩ (P∩P) = ∅ ∩ ∅ = ∅;
(3) Η elemei nem üreshalmazok:
(3.1) P∖Q = P∩Q ≠ ∅ ⇒ ∃x (x∈P ∧ x∉Q);
(3.2) Q∩P ≠ ∅ ⇒ ∃x (x∈P ∧ x∈Q);
(3.3) Q∖P = Q∩P ≠ ∅ ⇒ ∃x (x∉P ∧ x∈Q);
Mivel a (3.1), (3.2) és (3.3) feltételek mindegyikének teljesülnie kell ahhoz, hogy a Η halmazrendszer osztályozás legyen, ezért a 'P' és 'Q' halmazoknak legalább két-két elemük kell, hogy legyen, amelyek közül
– egy elem közös elem (vagyis mindkét halmaznak eleme),
– egy-egy elem pedig csak a 'P', ill. a 'Q' halmaznak eleme (a másik halmaznak nem).

(a2) A={a logikai készlet elemei^⇒}, P⊂A és Q⊂A tetszőleges (nem üres) halmazok
Η = {P∖Q, P∩Q, Q∖P, P∩Q}

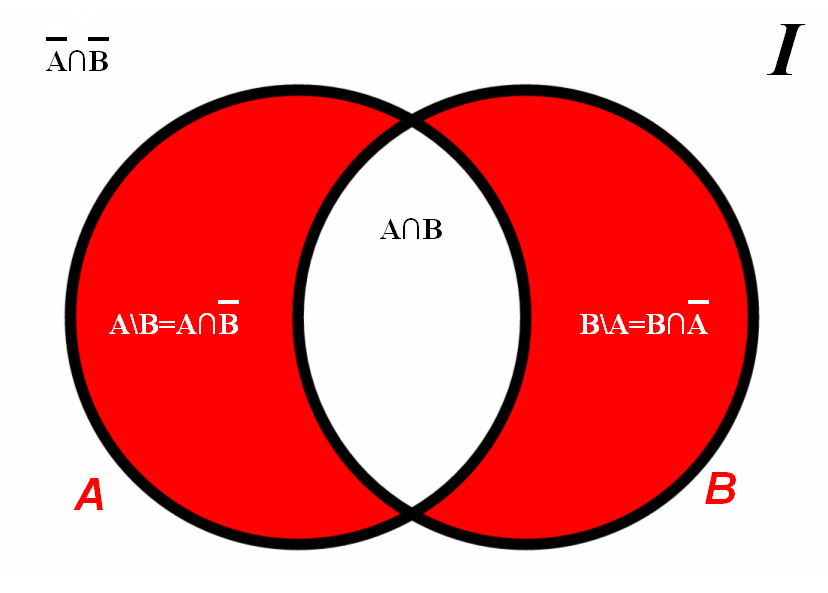
Általánosan igaz, hogy egy adott 'I' alaphalmaz és ennek két tetszőleges részhalmaza (A⊆I, B⊆I) esetén
I = A∖B ∪ B∖A ∪ A∩B ∪ A∩B = A∩B ∪ A∩B ∪ B∩A ∪ A∩B
teljesül, ahol az unióképzésben szereplő tagok páronként diszjunktak. (A formula könnyebb megjegyezhetősége érdekében az unióképzés egyes tagjait nem tettük zárójelbe, vagyis feltételezzük, a formula kiértékelésekor először minden esetben a metszetképzést hajtjuk végre.) Az 'I' alaphalmaz felbontását Venn-diagramon szemléltethetjük:

(b) A=ℤ
Η = {{páros egész számok}, {páratlan egész számok}} (megjegyzés: a nullát páros számnak tekintjük, mert osztható 2-vel^⇒)

(d) A=ℤ
Η = {{pozitív egész számok}, {negatív egész számok}}

(e) A=ℤ
Η = {{pozitív egész számok}, {nemnegatív egész számok}}

Vizsgálja meg az alábbi relációk tulajdonságait és válassza ki a rendezési relációkat!

(a) I = {egy osztály tanulóinak halmaza}
α = {(a,b) | a∈I, b∈I, 'a' több ötöst kapott a héten, mint 'b'}

(b) K = {egymásra rakott könyvek halmaza}
β = {(a,b) | a∈K, b∈K, az 'a' könyv a 'b' könyv felett van}

(d) M = {egy polcon levő könyvek halmaza}
β = {(a,b) | a∈K, b∈K, az 'a' könyv a 'b' könyv mellett van}

Adjon meg egy (vagy több) ekvivalenciarelációt és rendezési relációt az alábbi halmazokon! Adja meg és ábrázolja a relációkat!

(a) A = {veréb, ló, elefánt, sas, medve}

(b) A = {(5, 2), (8, 3), (4, 9), (7, 2), (11, 2), (13, 9)}

Ábrázolja Hasse-diagramon az alábbi részben rendezett halmazokat és határozza meg a legkisebb / legnagyobb, ill. minimális / maximális elemeket, ha léteznek!

(a) ({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; |) (vö. Dringó-Kátai 1986: 29; vö. az (1) (a1) feladattal^⇒)

(b) ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; |) (vö. Dringó-Kátai 1986: 29; vö. az (1) (a2) feladattal^⇒)

(d) ({1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}; |)