Matematika 1 - Gyakorló feladatok

Gyakorló feladatok:

Az alábbi táblázatban egy osztály tanulóinak az érdemjegyei szerepelnek.

név	matematika	ének	testnevelés	átlag	logikai érték
átlag

Legyen I={Tercsi, Fercsi, Kata, ...} a tanulók halmaza és T={matematika, ének, testnevelés, ...} a tantárgyak halmaza. Vezessük be a korábban már megismert "osztályozó" függvényt^⇒
jegy : IΧT→{1, 2, 3, 4, 5}
módon. Vegyük észre, hogy a fenti táblázat középső oszlopai éppen az osztályozó függvény aktuális értékeit adják meg.

Értelmezzük az 'M', 'E' és 'T' predikátumfüggvényeket a következőképpen:

M(x,i) ⇋ "az 'x' tanuló jegye matematikából 'i'"
E(x,j) ⇋ "az 'x' tanuló jegye énekből 'j'"
T(x,k) ⇋ "az 'x' tanuló jegye testnevelésből 'k'"

A fenti predikátumfüggvények az osztályozó függvény segítségével
    M(x,i) ⇋ jegy(x,"matematika")=i
    E(x,j) ⇋ jegy(x,"ének")=j
    T(x,k) ⇋ jegy(x,"testnevelés")=k
módon fejezhetők ki.

Értelmezze az alábbi összetett logikai kifejezéseket (formulákat), és határozza meg a kifejezések logikai értékét a bennük szereplő szabad változó (tanuló vagy jegy) különböző értékeire:

(a1) M(x,3)∨E(x,4) (Kik azok a tanulók, akik...)
(a2) M(x,5)∧E(x,4)
(a3) E(x,5)∧⌝T(x,4)
(a4.1) T(x,4)⊃E(x,5)
(a4.2) T(x,4)∧.T(x,4)⊃E(x,5)
(a5) M(x,5)≡E(x,5)

(b1) M(Tercsi,i)∨E(Tercsi,i)∨T(Tercsi,i) (Mik azok a jegyek, amelyeket...)
(b2) M(Tercsi,i)∨M(Fercsi,i)∨M(Kata,i)

(c1) ∃x (M(x,i))
(c2) ∃x (M(x,i)∧E(x,i))
(c3) ∃x (M(x,i)∧E(x,i)∧T(x,i))
(c4) ∃x (M(x,5)∧T(x,i))

(d1) (M(x,4)∨M(x,5))∧(T(x,4)∨T(x,5))
(d2) (M(x,4)∧E(x,5))∨(M(x,5)∧E(x,4))
(d3) M(x,5)⊃.(E(x,3)≡T(x,2))

(e1) jegy(x,"matek")=3 ∨ jegy(x,"enek")=4
(e2) jegy(x,"matek")=3 ∧ jegy(x,"enek")=4
(e3) ∃t (jegy("Tercsi",t)=i)
(e4) ∃x (jegy(x,t)<=2)
(e5) (jegy(x,"matek")+jegy(x,"enek")+jegy(x,"tesi"))/3>=3.5

(f1) ∃i M(x,i)⊃.(E(x,3)≡T(x,2))
(f2) ∃i∃j M(x,i)⊃.(E(x,j)≡T(x,2))
(f3) ∃i∃j∃k M(x,i)⊃.(E(x,j)≡T(x,k))

Ha a logikai kifejezésben szabad változóként egy tanuló szerepel, a fenti táblázat utolsó oszlopában értékelje ki soronként a fent megadott logikai kifejezéseket! Ezután határozza meg a logikai kifejezések igazsághalmazát!

Például ha van egy olyan sor a táblázatban, amelyben Kata matekből jeles, énekből közepes és tesiből elégséges, azaz

teljesül, akkor x="Kata", i=5, j=3 és k=2 miatt a
M(x,i)⊃.(E(x,j)≡T(x,k)) ⇋ "Ha az 'x' tanuló jegye matekből 'i', akkor ebből az következik, hogy az 'x' tanuló pontosan akkor kap énekből 'j' jegyet, ha tesiből 'k' jegyet szerzett."
összetett logikai kifejezés az adott sorban igaz. Emiatt például a
    ∃i∃j∃k M(x,i)⊃.(E(x,j)≡T(x,k))
logikai kifejezés igazsághalmazának "Kata" eleme.

Vegyük észre, hogy ha egy másik tanulót választunk (pl. legyen x="Mari"), akkor
– ha az adott tanuló matekből nem jelest kapott, a logikai kifejezés biztosan igaz lesz;
– ha az adott tanuló matekből jelest kapott, a logikai kifejezés csak akkor lesz igaz, ha vagy az ének és tesi jegye közepes és elégséges, vagy a tanuló mindkét tárgyból ezektől különböző jegyet kapott.

Ha a logikai kifejezésben szabad változóként egy jegy szerepel, akkor használjon egy segédtáblázatot. Például a (b2) feladatban ez a következőképpen készíthető el:

jegy	M(Tercsi,i)	M(Fercsi,i)	M(Kata,i)	...	logikai érték
1
2
3
4
5

A '...'-tal jelölt oszlop azt jelzi, hogy más logikai kifejezések esetén több segédoszlopra is szükség lehet. (Például a (c1) pontban szereplő feladat esetén elvileg annyi segédoszlopra lenne szükség, ahány tanuló van az osztályban.)

[kieg.] Az 'M', 'E' és 'T' predikátumfüggvények és a tanult logikai műveletek felhasználásával keressen olyan összetett logikai kifejezéseket, amelyek minden tanuló esetén (azaz a táblázat minden sorában) teljesülnek! (Ez megfelel annak, hogy az adott táblázatban fennálló törvényeket keressünk. Azonban ezek egy másik táblázatban már nem biztos, hogy teljesülnek, vagyis nem, vagy nem feltétlenül logikai törvények.)

Tekintsük például az alábbi táblázatot:

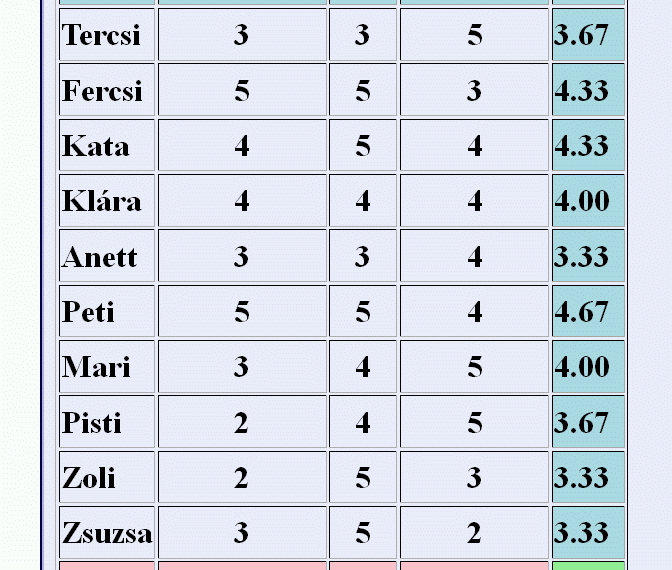
(1) A táblázatból látszik, hogy ha egy tanuló tesiből közepes, akkor énekből jeles. Tehát k=3 és j=5 választása mellett a
    T(x,3)⊃E(x,5)
logikai kifejezés igaz bármilyen 'x' választása esetén, azaz
    |∀x(T(x,3)⊃E(x,5))|=1
teljesül.

(2) A táblázatból az is látszik, hogy ha egy tanuló matekből jeles, akkor énekből jeles, és tesiből vagy közepes, vagy jó. Tehát például i=5, j=5 és k=3, ill. k=4 választása mellett az
    M(x,5)⊃.E(x,5)∧(T(x,3)∨T(x,4))
összetett logikai kifejezés igaz bármilyen 'x' választása esetén, azaz
    |∀x(M(x,5)⊃.E(x,5)∧(T(x,3)∨T(x,4)))|=1
teljesül.

Vizsgáljunk meg az alábbi naplórészletet, amely a tanulók jegyeit tartalmazza matematikából, énekből és testnevelésből.

sorszám	dátum	név	tárgy	jegy

Értelmezzük a 'datum', 'nev', 'targy' és 'jegy' függvényeket a következőképpen:

datum(i) ⇋ "az 'i'-dik sorban szereplő dátum"
nev(i) ⇋ "az 'i'-dik sorban levő tanuló neve"
targy(i) ⇋ "az 'i'-dik sorban levő tárgy neve"
jegy(i) ⇋ "az 'i'-dik sorban szereplő jegy"

A fent definiált függvények használatával adja meg azokat a logikai kifejezéseket, amelyekhez az alábbiakban megadott 'I' igazsághalmazok tartoznak!

(a1) Klára jegyei matematikából
(a2) Klára jegyei matematikából és énekből
(a3) Klára jegyei (bármilyen tárgyból)

(b1) azoknak a tanulóknak a nevei, akik jelest kaptak testnevelésből
(b2) azoknak a tanulóknak a nevei, akik közepesnél jobb jegyet kaptak matematikából
(b3) azoknak a tanulóknak a nevei, akik jónál rosszabb jegyet kaptak énekből és jelest kaptak testnevelésből

(c1) azoknak a tárgyaknak a nevei, amelyekből Kata jót vagy jelest kapott
(c2) azok a jegyek, amelyeket a tanulók matematikából kaptak
(c3) azoknak a tanulóknak a nevei, akik valamilyen tárgyból elégtelent vagy elégségest kaptak