JavaScript alapok

Tartalomjegyzék

1. bevezetés: egy egyszerű JavaScript program ("Hello!" kiírása)
2. változók használata
   • gyakorló feladatok
3. ciklusok
   • gyakorló feladatok (1)
   • gyakorló feladatok (2)
4. elágazások
   • gyakorló feladatok
5. függvények
   • gyakorló feladatok
6. alkalmazás: logikai igazságtáblázatok
   • gyakorló feladatok
7. alkalmazás: kombinatorikai feladatok
   • gyakorló feladatok
8. alkalmazás: egyéb alkalmazások
   • sorozatelemek kiválogatása
   • gyakorló feladatok
   • aritmetika, számelmélet
   • gyakorló feladatok

1. nyelvi elemek
2. adatok bevitele és kiírása
3. vezérlési szerkezetek
4.  
5. ajánlott irodalom, felhasznált források
6. további gyakorló feladatok

A példákhoz használt online JavaScript interpreter:

Online JavaScript Interpreter by Peter Jipsen, Chapman University (January 2013).
http://math.chapman.edu/~jipsen/js/ (2020-11-19)

Megjegyzés: Ha a fenti link valamilyen oknál fogva nem működik, használjuk az alábbi linket.

A JavaScript programok folyamatábráját megjeleníthetjük az alábbi webes alkalmazás segítségével:

Live code editor. Created by Bogdan Lyashenko.
https://bogdan-lyashenko.github.io/js-code-to-svg-flowchart/docs/live-editor/index.html (2022-10-02)

A folyamatábra a 'for' ciklust nem megfelelően ábrázolja, ezért ajánlott a 'for' ciklust tartalmazó programrészleteket mindig átírni 'while' ciklusra, mielőtt megjelenítenénk a program folyamatábráját.

Ismerkedés a JavaScript nyelvvel

egy egyszerű JavaScript program

/* 1. program */
writeln("Hello!");

Általában bármilyen programozási nyelvvel kezdünk el ismerkedni, az első lépés mindig egy "Hello!" (vagy "Hello, World!") kiírása. A JavaScript eredetileg a Netscape Navigator böngészőprogram programozási nyelve volt, de manapság már egy önálló, magas szintű programozási nyelv (bár a legtöbb JavaScript programot ma is böngészőprogramok számára írják). A JavaScript utasításokat rendszerint egy program, az ún. JavaScript interpreter egyenként hajtja végre, azonban a program végrehajtásának feltétele, hogy a JavaScript utasítások nyelvileg, szintaktikailag helyesen legyenek megadva.

Tanuljuk meg:

• Egy JavaScript programban a /* ... */ jelek között megjegyzéseket helyezhetünk el. A megjegyzések segítségével magyarázatokat fűzhetünk a programkódhoz.
• Egy JavaScript program utasításokból áll, amelyeket pontosvesszővel (;) zárunk le. Egy sorban több utasítás is állhat, de az áttekinthetőség érdekében legtöbbször hasznosabb, ha soronként egy utasítást adunk meg.
• Az egyik leggyakrabban használt utasítás az, amikor egy eljárást (alprogramot, ill. a JavaScript nyelvben függvényt) indítunk el, "hívunk meg". A példában a 'writeln' eljárást hívjuk meg writeln("Hello!"); módon. Egy eljárás legfontosabb jellemzői:
  • Az eljárásnak egyedi neve van, amellyel az eljárást azonosítjuk. A példában az eljárás neve 'writeln'.
  • Az eljárásnak lehetnek paraméterei, amelyek segítségével az eljárás számára bemeneti, input adatokat adhatunk meg. Az input adatokat az eljárás neve után, zárójelek között adjuk meg, "adjuk át" az eljárás számára. Az input adatokat az eljárás a működése során felhasználja. A példában ilyen input adat a "Hello!" karakterlánc vagy string, amelyet idézőjelek (esetleg aposztrófok) között adunk meg. A 'writeln' eljárás a meghíváskor a számára átadott "Hello!" stringet kiírja a képernyőre.
    • Vannak olyan eljárások, amelyek meghívásakor nem feltétlenül kell paramétereket megadnunk. Ilyenkor a zárójelek között nem adunk meg semmit. Például a writeln(); utasítás egy üres sort ír ki a képernyőre.
  • Az eljárás utasításokból áll, amelyeket az eljárás elindításakor (vagy meghívásakor) a JavaScript interpreter végrehajt, majd visszatér az eljárás meghívása után soron következő utasításhoz. A 'writeln' eljárás a JavaScript nyelv egy beépített ("standard") eljárása, amely a nyelv részét képezi. Számos más standard JavaScript eljárás és függvény áll rendelkezésünkre, amelyek közül egyre többet fogunk majd használni.

/* 2. program */
writeln("Hello!");
writeln();
writeln("------");

A fenti program három JavaScript utasításból áll. Mindhárom utasítás a 'writeln' eljárást hívja meg (kétszer string típusú paraméterrel, egyszer paraméter nélkül). A 'writeln' eljárás meghívásakor a böngésző JavaScript interpretere ("motorja")

• átadja a meghíváskor megadott "Hello!" értéket a 'writeln' eljárás számára, és
• végrehajtja a 'writeln' eljárás utasításait (ami esetünkben azt eredményezi, hogy az interpreter kiírja a meghíváskor megadott paraméter értékét és soremelést hajt végre), majd
• "visszatér" az eljárást meghívó főprogramba, és
• a főprogram végrehajtása a 'writeln' eljárás meghívása után soron következő utasítással folytatódik.

változók használata

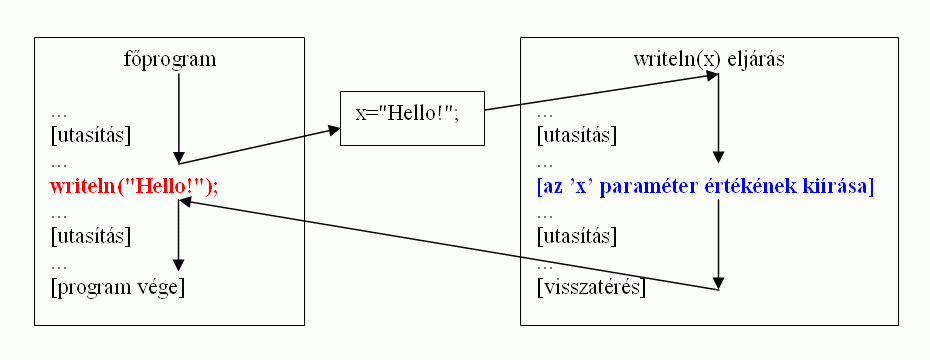
/* 3. program */
var s;
s="Hello!";
writeln(s);
s="Hello, World!";
writeln(s);
writeln();
writeln("------");

A programban a 'var' utasítással egy 's' nevű változót hozunk létre, majd az '=' operátor segítségével értéket adunk a változónak. Innentől kezdve az 's' változó addig tárolja a megadott string típusú értéket ("Hello!"), amíg azt egy másik értékadó utasítással meg nem változtatjuk.

A 'writeln' eljárás paramétereként nemcsak input értékeket adhatunk meg, hanem változókat is. Ebben az esetben az eljárás a változó értékét fogja kiírni.

/* 4. program */
var x,y,z;
x=1;
writeln(x);
y=2;
writeln(y);
z=x+y;
writeln(z);
writeln("------");

A létrehozott változók tárolhatnak számokat, numerikus típusú értékeket is.A számok között műveleteket (pl. összeadást) is végezhetünk, és a művelet eredményét kiírathatjuk vagy eltárolhatjuk egy újabb változóban.

/* 5. program */
var s1,s2,s3;
s1="Hello";
writeln(s1);
s2="World";
writeln(s2);
s3=s1+", "+s2+"!";
writeln(s3);
writeln();
writeln("------");

A karakterlánc vagy string típusú értékek között használhatjuk az összefűzés vagy konkatenáció ('+') műveletét. Ezzel mind string típusú értékek (pl. ", " vagy "!"), mind string típusú változók (pl. s1, s2) összekapcsolhatók.

/* 6. program */
var x,y,z;
x=1;
writeln("x = "+x);
y=2;
writeln("y = "+y);
z=x+y;
writeln("x+y = "+x+"+"+y+" = "+z);
writeln("------");

A fenti, 6. program képernyőképe a következő:

/* 7. program */
var x,y,z;
x=1;
y=2;
z=x+y;
writeln("x+y = "+x+"+"+y+" = "+z);
z=x-y;
writeln("x-y = "+x+"-"+y+" = "+z);
z=x*y;
writeln("x*y = "+x+"*"+y+" = "+z);
z=x/y;
writeln("x/y = "+x+"/"+y+" = "+z);
writeln("------");

Az összeadás mellett más műveletek operátorai is rendelkezésre állnak. A fenti programban a számok közötti alapműveletek szerepelnek: az összeadás (+), a kivonás (-), a szorzás (*) és az osztás (/). Például az 1/2 művelet eredménye 0.5 (a programozási nyelvekben szinte mindig tizedespontot használunk).

Tanuljuk meg:

• A JavaScript programozási nyelvben a számok és a stringek (karakterláncok) tárolására változókat használunk. Egy változó legfontosabb jellemzői:
  • a változó neve;
  • a változó (aktuális) értéke, azaz a változóban tárolt érték;
  • a változó típusa, amely megegyezik az általa tárolt érték típusával (a JavaScript ún. nem típusos programozási nyelv, a változók típusa attól függ, milyen értéket adunk nekik).
• A JavaScript programozási nyelvben a 'var' utasítás segítségével hozhatunk létre új változókat.
• A JavaScript programozási nyelvben az '=' értékadó utasítás segítségével adhatunk egy változónak új értéket. (Az értékadás mindig törli a változó korábbi értékét.)
• A JavaScript programozási nyelvben a változókon különböző műveleteket hajthatunk végre:
  • a '+' operátor számok közötti összeadást és stringek közötti konkatenációt (összefűzést) jelent;
  • a '-' operátor számok közötti kivonást jelent;
  • a '*' operátor számok közötti szorzást jelent;
  • a '/' operátor számok közötti osztást jelent.

Gyakorló feladatok:

(1) Futtassa le a korábbi (1-7) programokat, és változtasson rajtuk úgy, hogy minden sorban jelenjen meg valamilyen módosítás, és minden programhoz legalább öt új sort adjon hozzá!

Lehetséges változtatások:

• a változók átnevezése,
• új változók bevezetése,
• összetett (több műveletet és zárójeleket is tartalmazó) képletek kiszámítása, pl.
  • egy háromszög kerülete, területe,
  • különböző testek felszíne, térfogata,
  • ...
• a kiírások szövegének és tartalmának (a benne szereplő változóknak, kifejezéseknek) a megváltoztatása,
• ...

(2) Hozzon létre három változót, és adja nekik értékül a "Tercsi", "Fercsi" és "Kata" neveket. Írassa ki külön sorokban a nevek összes lehetséges permutációját (szögletes zárójelek között és a neveket vesszővel elválasztva). Például a következőképpen:

var t="Tercsi";
var f="Fercsi";
var k="Kata";

writeln("["+t+","+f+","+k+"]");
writeln("["+t+","+k+","+f+"]");
...

A megoldás képernyőképe a következő lehet:

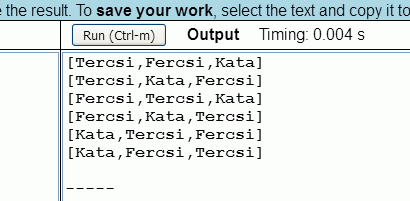
Később adunk egy olyan megoldást is, amely egymásba ágyazott ciklusok segítségével írja ki a megadott keresztnevek összes permutációját.

(3) Írassa ki a négyzetszámok és köbszámok táblázatát 1-től 10-ig!

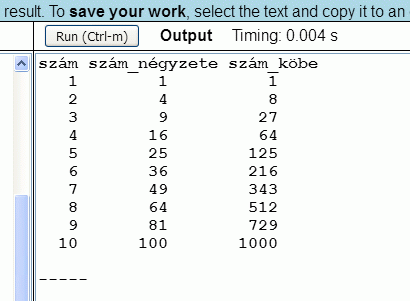
A megoldás képernyőképe a következő:

ciklusok

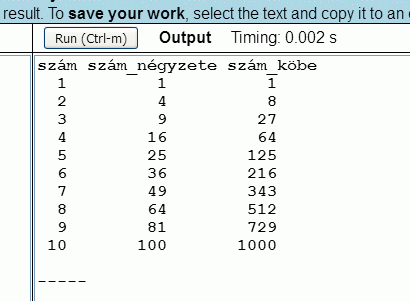
A JavaScript lehetővé teszi meghatározott utasítássorozatok többszöri megismétlését egy adott logikai feltétel teljesülésétől függően. Ehhez egy ún. vezérlő ciklus elkészítésére van szükség, amit vagy a 'for' (kb. "ismételd annyiszor, amíg ...") vagy a 'while' (kb. "ismételd, amíg ...") kulcsszavak segítségével valósíthatunk meg.

/* 8.1. program */
var k,n;
k=1;
n=10;

var i=1;
while(i<=n) {
 writeln(i+". szám: "+k);
 k=k+1;
 i=i+1;
 }

writeln();
writeln("_______________");

/* 8.2. program */
var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+k);
 k=k+1;
 }

writeln();
writeln("-----");

A fenti programok az első 10 egész számot írják ki egymás alá (némi magyarázó szöveggel egyetemben). Ezt természetesen megtehetnénk a következőképpen is:

writeln("1. szám: 1");
writeln("2. szám: 2");
writeln("3. szám: 3");
writeln("4. szám: 4");
writeln("5. szám: 5");
writeln("6. szám: 6");
writeln("7. szám: 7");
writeln("8. szám: 8");
writeln("9. szám: 9");
writeln("10. szám: 10");


Ha a 8.1. és 8.2. programokhoz teljesen hasonlóan szeretnénk eljárni, a fenti utasítások helyett a következőket is írhatnánk:

writeln(1+". szám: "+1);
writeln(2+". szám: "+2);
writeln(3+". szám: "+3);
writeln(4+". szám: "+4);
writeln(5+". szám: "+5);
writeln(6+". szám: "+6);
writeln(7+". szám: "+7);
writeln(8+". szám: "+8);
writeln(9+". szám: "+9);
writeln(10+". szám: "+10);


Azonban már komolyabb nehézségbe ütköznénk, ha egy olyan programot kellene készítenünk, amely pl. az első 100 számot írja ki (éppen másolgathatnánk az utasításokat, de azért a türelemnek is van határa :) ). Ha pedig a programtól azt várnánk el, hogy 'n' darab számot írjon ki, például egy adott 'k' számtól kezdve, akkor minden különböző 'k' értékre állandóan át kellene írnunk a 'writeln' utasítások paramétereit. Ezért a 8. programot úgy készítettük el, hogy a 'k' és az 'n' változóknak különböző kezdőértéket adva a program mindig 'n' darab számot ír ki a 'k' számtól kezdve.

A programok képernyőképe a következő:

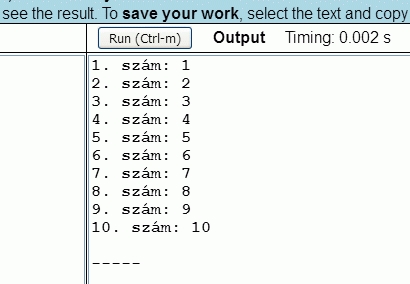
A 8.1. program alapját a

var i=1;
while(i<=n) {
 ...
 i=i+1;
 }


szerkezettel megvalósított ún. elöltesztelő ciklus jelenti, amely a JavaScript programozási nyelv egyik ismétlő (iterációs) szerkezete. Ezt használva tudjuk elérni, hogy esetünkben a {...} kapcsos zárójelek között megadott 'writeln' utasításokat a program helyettünk hajtsa végre a (...) zárójelek között megadott minta szerint, és pontosan addig ismételje őket (bizonyos szabályszerű változtatásokkal), amíg kell.

A 'while' ciklus a következő elemekből tevődik össze:

• a var i=1; utasítás az 'i' ciklusváltozó kezdőértékét állítja be
• a while(...) rész a ciklus fejrésze, amelyben a ciklusfeltétel meghatározza, hányszor fusson le a ciklus
  • az 'i' változó a ciklusváltozó, amelynek a kezdőértékét korábban megadtuk
  • az 'n' változó egy másik változó, amely azt adja meg, hányszor kell a ciklust megismételni
  • az i<=n kifejezés a ciklusfeltétel, amely alapján a program eldönti, megismételje-e a ciklusmagban szereplő utasításokat
    • ha a ciklusfeltétel igaz, a ciklus a {...} kapcsos zárójelek között megadott utasítások végrehajtásával folytatódik
    • ha a ciklusfeltétel hamis, a ciklus befejeződik, és a program a ciklus után következő utasítással folytatódik
• a kapcsos zárójelek {...} közötti rész a ciklus blokkja (az ún. ciklusmag), amely a ciklus által ismételt utasításokat tartalmazza
  • az i=i+1 utasítás a ciklusváltozó növelését valósítja meg; ez a ciklusmag utolsó utasítása

A ciklus lényege a ciklus blokkjában szereplő utasítások ismétlése. A legfontosabb feladat annak a beállítása, hogy a program hányszor hajtsa végre a ciklusblokkot. A ciklus a következő lépések végrehajtását valósítja meg:

1. a ciklusváltozó kezdőértékének beállítása
2. a ciklusfeltétel megvizsgálása
   • ha a feltétel igaz, a 3. lépés végrehajtása
   • ha a feltétel hamis, a ciklus végrehajtásának befejezése, azaz ugrás a 6. lépésre
3. a ciklusblokk (vagy ciklusmag) utasításainak végrehajtása
4. a ciklusváltozó értékének növelése eggyel
5. visszaugrás a 2. lépésre
6. a program folytatása

Nagyon fontos annak a megértése, hogy a ciklusváltozó kezdőértékének beállításával, a ciklusfeltétellel, és a ciklusváltozó növelésével tudjuk beállítani, pontosan hányszor ismétlődjön meg a ciklusblokk (vagyis hányszor hajtódjon végre a ciklusblokkban szereplő utasítások sorozata, szekvenciája).

A 8.2. program alapját a

for(var i=1;i<=n;i++) {
 ...
 }


szerkezettel megvalósított ún. rögzített lépésszámú ciklus jelenti, amely a JavaScript programozási nyelv legfontosabb ismétlő (iterációs) szerkezete. Ezt használva tudjuk elérni, hogy esetünkben az egyes 'writeln' utasításokat a program helyettünk hajtsa végre egy megadott minta szerint, és pontosan addig ismételje őket (bizonyos szabályszerű változtatásokkal), amíg kell.

A 'for' ciklus a következő elemekből tevődik össze:

• a for(...) rész a ciklus fejrésze, ahol azt állítjuk be, hányszor fusson le a ciklus
  • az 'i' változó a ciklusváltozó
  • az i=1 utasítás a ciklusváltozó kezdőértékének megadása
  • az i<=n kifejezés a ciklusfeltétel
  • az i++ utasítás a ciklusváltozó növelése
    • az i++ utasítás az i=i+1 utasítás rövid formája
      (figyelmeztetés: az i++ utasítás után, mivel az a 'for' ciklus fejrészének utolsó utasítása, nem szabad pontosvesszőt tenni!)
• a kapcsos zárójelek {...} közötti rész a ciklus blokkja (az ún. ciklusmag), amely a ciklus által megismételt utasításokat tartalmazza
  (figyelmeztetés: a { kezdő kapcsos zárójel előtt nem szabad, a } záró kapcsos zárójel után nem szükséges pontosvesszőt tenni!)

A ciklus lényege a ciklus blokkjában szereplő utasítások ismétlése. A legfontosabb feladat annak a beállítása, hogy a program hányszor hajtsa végre a ciklusblokkot. A ciklus a következő lépések végrehajtását valósítja meg:

1. a ciklusváltozó kezdőértékének beállítása;
2. a ciklusfeltétel megvizsgálása
   • ha a feltétel igaz, a 3. lépés végrehajtása;
   • ha a feltétel hamis, a ciklus végrehajtásának befejezése, azaz ugrás a 6. lépésre
3. a ciklusblokk (vagy ciklusmag) utasításainak végrehajtása;
4. a ciklusváltozó növelése (ha a ciklusfejben 'i++' szerepel, akkor az 'i' ciklusváltozó értékét eggyel növeljük);
5. visszaugrás a 2. lépésre.
6. a program folytatása

Ismételjük meg, hogy most is a ciklusváltozó kezdőértékének beállításával, a ciklusfeltétellel, és a ciklusváltozó növelésével tudjuk beállítani, pontosan hányszor ismétlődjön meg a ciklusblokk (vagyis hányszor hajtódjon végre a ciklusblokkban szereplő utasítások sorozata, szekvenciája).

Végezetül jegyezzük meg, hogy összehasonlítva a 8.1. és a 8.2. programokat, megállapíthatjuk, hogy a 'for' ciklus a 'while' ciklus tömör formájának is tekinthető. A 'for' ciklust minden esetben meg tudjuk valósítani egy 'while' ciklus segítségével; azonban a 'for' ciklus előnyei közé tartozik, hogy
– a ciklusváltozó növelését már a fejrészben meg kell adnunk, így elkerülhetjük a végtelen ciklust (ami könnyen előfordulhat pl. a 'while' ciklus használatakor, ha kihagyjuk a ciklus végén a ciklusváltozó növelését);
– a 'continue' utasítást nagyon kényelmesen használhatjuk, ha a ciklusmag hátralevő részét ki akarjuk hagyni.

Gyakorlásképpen írassuk ki az első 15 négyzetszámot, azaz a {1, 4, 9, 25, ...} számsorozat első 15 elemét:

/* 9.1. program */
var k,n;
k=1;
n=15;

var i=1;
while(i<=n) {
 k=i*i;
 writeln(i+". szám: "+k);
 i=i+1;
 }

writeln();
writeln("____________");

/* 9.2. program */
var k,n;
k=1;
n=15;

for(var i=1;i<=n;i++) {
 k=i*i;
 writeln(i+". szám: "+k);
 }

writeln();
writeln("-----");

Írassuk ki az s_i=(1+i)/i sorozat első 15 elemét két tizedesjegy pontossággal:

/* 10.1. program */
var k,n;
k=1;
n=15;

var i=1;
while(i<=n) {
 k=(1+i)/i;
 writeln(i+". szám: "+k.toFixed(2));
 i=i+1;
 }

writeln();
writeln("_____________");

/* 10.2. program */
var k,n;
k=1;
n=15;

for(var i=1;i<=n;i++) {
 k=(1+i)/i;
 writeln(i+". szám: "+k.toFixed(2));
 }

writeln();
writeln("-----");

Tanuljuk meg, hogy egy számot adott számú tizedesjegyre a .toFixed(tizedesjegyek_szama) függvény segítségével kerekíthetjük (pl. (1/3).toFixed(2) értéke 0.33, (7/6).toFixed(3) értéke 1.167, (−5/9).toFixed(4) értéke -0.5556 stb.).

A 10. program képernyőképe a következő:

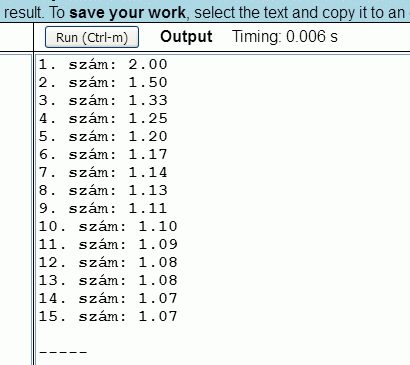
Ezek után írassuk ki 2 első 20 hatványát, azaz az {1, 2, 4, 8, 16, ...} számsorozat első 20 elemét. Vegyük észre hogy a sorozat elemeit a 'k' változóban tároljuk. A sorozat első elemének beállítása (k=1;) után a sorozat következő elemét minden esetben az előző elem 2-vel történő szorzásával kapjuk meg (k=k*2).

/* 11.1. program */
var k,n;
k=1;
n=20;

var i=1;
while(i<=n) {
 writeln(i+". szám: "+k);
 k=k*2;
 i=i+1;
 }

writeln();
writeln("__________");

/* 11.2. program */
var k,n;
k=1;
n=20;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+k);
 k=k*2;
 }

writeln();
writeln("-----");

Végül írassuk ki d=3 növekmény mellett az s₁=1, s_i=s_i−1+d (i>1, i∈ℕ) számtani sorozat első 10 elemét, valamint a számtani sorozat első 10 elemének összegét:

/* 12.1. program */
var d,k,n,sum;
d=3;
k=1;
n=10;
sum=0;

var i=1;
while(i<=n) {
 writeln(i+". szám: "+k);
 sum=sum+k;
 k=k+d;
 i=i+1;
 }

writeln();
writeln("Az első "+n+" elem összege: "+sum);

writeln();
writeln("_____________");

/* 12.2. program */
var d,k,n,sum;
d=3;
k=1;
n=10;
sum=0;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+k);
 sum=sum+k;
 k=k+d;
 }

writeln();
writeln("Az első "+n+" elem összege: "+sum);

writeln();
writeln("-----");

A programban annyi újdonság van az előzőekhez képest, hogy egy 'sum' nevű változóban állítottuk elő az első 'n' sorozatelem összegét:

• a ciklus előtt a 'sum' változó kezdőértékét 0-ra állítottuk be sum=0; módon;
• a ciklusmagban a 'sum' változó aktuális értékéhez hozzáadtuk az aktuális sorozatelem értékét ('k'), és az eredményt eltároltuk a 'sum' változóban sum=sum+k; módon;
• majd az aktuális (i-dik) sorozatelem értékéből ('k') meghatároztuk a sorozat következő (i+1-dik) elemét k=k+d; módon.

Most foglaljuk össze az eddigieket. Az előző programok a 'while' és a 'for' ciklus segítségével különböző számsorozatok első 'n' elemét írták ki. A programokban a sorozatok i-dik elemét kétféleképpen számoltuk ki:

(1) A sorozat elemeit egy képlet segítségével adtuk meg, közvetlenül az elem sorszáma ('i') segítségével (9-10. programok). A sorozat i-dik elemét egy 'k' változóban tároltuk. A 'k' változó értékét a 'writeln' kiíró utasítás előtt állítottuk be, az 'i' ciklusváltozó aktuális értékét felhasználva (ilyenkor a 'k' változó kezdőértékének nincs különösebb jelentősége, mert a 'k' változó értékét a 'writeln' utasítás előtt mindig beállítjuk).

(2) A sorozat elemeit a megelőző sorozatelem segítségével, ún. rekurzív módon adtuk meg (11-12. programok). Ekkor
– először kiírattuk a sorozat i-dik elemét tartalmazó 'k' változó aktuális értékét, majd
– a 'writeln' kiíró utasítás után beállítottuk a 'k' változó értékét úgy, hogy az értékadás után már a sorozat következő, (i+1)-dik elemét tartalmazza. Ehhez az értékadásban (az = értékadó operátor jobb oldalán) felhasználtuk a 'k' változó korábbi értékét, amely az értékadáskor a sorozat előző, i-dik elemét tartalmazta.

Azokat a rekurzív módon megadott sorozatokat, amelyekben a sorozat i-dik elemének megadásakor az (i−1)-dik és az (i−2)-dik elemre is szükségünk van, egy 'm' segédváltozó segítségével tudjuk a legegyszerűbben kiíratni.

Például tekintsük az alábbi sorozatot:

    s₁=1; s₂=1; s_i=s_i−1+s_i−2 (i>2, i∈ℕ).

A sorozat elemei: {1, 1, 2, 3, 5, 8, ...} (ez ún. Fibonacci-sorozat).

Az alábbi program a Fibonacci-sorozat első 10 elemét íratja ki:

/* 13.1. program */
var m,k,n;
m=1; // sorozat első eleme
k=1; // sorozat második eleme
n=10;

var i=1;
writeln(i+". szám: "+m);

i=2;
while(i<=n) {
 writeln(i+". szám: "+k);
 k=k+m; // sorozat következő (i+1-dik) eleme
 m=k-m; //  // sorozat előző (i-dik) eleme
 i=i+1;
 }

writeln();
writeln("___________");

/* 13.2. program */
var m,k,n;
m=1;
k=1;
n=10;

writeln(1+". szám: "+m);

for(var i=2;i<=n;i++) {
 writeln(i+". szám: "+k);
 k=k+m;
 m=k-m;
 }

writeln();
writeln("-----");

Vegyük észre, hogy az 'm' változóban mindig a sorozat 'k'-dik elemét megelőző elemét tároljuk. Mivel a 'k' változóra vonatkozó k=k+m; értékadás után 'k' a sorozat (i+1)-dik elemét fogja tartalmazni, az előző, i-dik elemet újra elő kell állítanunk, hogy tárolni tudjuk 'm'-ben. Ez egy 'temp' nevű segédváltozó bevezetésével is megoldható:

/* 14.1. program */
var m,k,n;
m=1;
k=1;
n=10;

var i=1;
writeln(i+". szám: "+m);

i=2;
while(i<=n) {
 writeln(i+". szám: "+k);
 var temp;
 temp=k;
 k=k+m;
 m=temp;
 i=i+1;
 }

writeln();
writeln("___________");

/* 14.2. program */
var m,k,n;
m=1;
k=1;
n=10;

writeln(1+". szám: "+m);

for(var i=2;i<=n;i++) {
 writeln(i+". szám: "+k);
 var temp;
 temp=k;
 k=k+m;
 m=temp;
 }

writeln();
writeln("-----");

Mivel a 'temp' változót csak a 'for' ciklus ciklusmagjában használjuk a sorozat i-dik elemének ideiglenes tárolására, érdemes ott létrehozni.

Gyakorló feladatok (1):

Készítse el az alábbi sorozatok első 'n' elemét kiíró programokat. Készítse el mindegyik program folyamatábráját is!

(1) n=20; s_i=3*i

(2) n=10; s₀=1; s₁=1; s_i=s_i−1*i (i>1, i∈ℕ); a sorozat elemei: {1, 1, 2, 6, 24, ...} (faktoriálisok sorozata, s_i=i!)

(3) n=9; s_i=(2*i²−3*i+4)

(4) n=8; s_i=(i²−7*i+12)/(3*i−6)

(5) n=10; q=0.5; s₁=1; s_i=s_i−1*q (i>1, i∈ℕ) (mértani sorozat)

(6) n=11; s₁=3; s_i=2*s_i−1 (i>1, i∈ℕ); a sorozat elemei: {3, 6, 12, 24, ...}

(7) n=12; s₁=3; s_i=3*s_i−1²−4*s_i−1+5 (i>1, i∈ℕ)

(8) n=15; s₁=0, s₂=1, s_i=(s_i−1+s_i−2)/2 (i≥3, i∈ℕ)

Végül két, valamivel nehezebb feladat:

(9) n=10; s₁=1; s_i=s_i−1+(i−1) (i>1, i∈ℕ); a sorozat elemei: {1, 2, 4, 7, 11, ...} (növekményes sorozat)

(10) n=12; s₁=2; s_i=s_i−1+(2*i−1) (i>1, i∈ℕ); a sorozat elemei: {2, 5, 10, 17, ...} [tipp: alakítsuk át a sorozat növekményét megadó (2*i−1) kifejezést (2*i−1) = (2*(i−1+1)−1) = (2*(i−1)+2−1) = (2*(i−1)+1) módon]

Az utolsó két feladat egy 'm' segédváltozó segítségével is megoldható, ha a sorozatok növekményét egy új, t_i sorozatnak tekintjük, és ennek az elemeit állítjuk elő 'm'-ben.

Például a (9) feladat esetében a növekményt előállító sorozat
    t₁=0; t_i=i−1 (i>1, i∈ℕ), a sorozat elemei: {0, 1, 2, 3, ...}.
Vegyük észre, hogy ez a t_i sorozat rekurzív módon is megadható
   t₁=0; t_i=t_i−1+1 (i>1, i∈ℕ)
módon, azaz az 's' sorozat i-dik elemének előállításához szükséges növekményt úgy kapjuk meg, hogy a növekmény előző értékéhez egyet mindig hozzáadunk. Az így definiált t_i sorozattal az eredeti sorozat
   s₁=1; s_i=s_i−1+t_i (i>1, i∈ℕ)
módon állítható elő.

Nézzük meg a (9)-es feladat megoldását ilyen módon:

/* 15.1. program */
var m,k,n;
m=0; // növekmény
k=1;
n=10;

var i=1;
while(i<=n) {
 writeln(i+". szám: "+k);
 m=m+1; // következő növekmény
 k=k+m; // következő sorozatelem
 i=i+1;
 }

writeln();
writeln("__________");

/* 15.2. program */
var m,k,n;
m=0;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+k);
 m=m+1;
 k=k+m;
 }

writeln();
writeln("-----");

A program a sorozatelemek növekményét az 'm' változóban állítja elő. A következő sorozatelem növekményét az 'm' változó értékének növelésével kapjuk meg (m=m+1;).

Gyakorló feladatok (2):

Módosítsa az előző gyakorló feladatokban szereplő sorozatok első 'n' elemének kiírását megvalósító programokat úgy, hogy azok az elemek összegét is kiírják! Készítse el most is mindegyik program folyamatábráját!

Utolsó feladatként készítsük el ciklussal az első 'n' négyzetszám és köbszám táblázatát! Emlékezzünk rá, hogy a feladatot korábban már megoldottuk, így a ciklusmagban szereplő 'writeln' utasítás mintája adott, pusztán a kiírandó értékeket kell a megfelelő változókkal helyettesíteni.

/* 16.1. program */
var k,k1,k2,n;
k=1;
k1=1;
k2=1;
n=10;

writeln("szám szám_négyzete szám_köbe");

var i=1;
while(i<=n) {
 k=i;
 k1=i*i;
 k2=i*i*i;
 writeln("  "+k+"         "+k1+"          "+k2);
 i=i+1;
 }

writeln();
writeln("____________");

/* 16.2. program */
var k1,k2,n;
n=10;

writeln("szám szám_négyzete szám_köbe");

for(var i=1;i<=n;i++) {
 k1=i*i;
 k2=k1*i;
 writeln("  "+i+"         "+k1+"          "+k2);
 }

writeln();
writeln("-----");

A megoldás képernyőképe a következő:

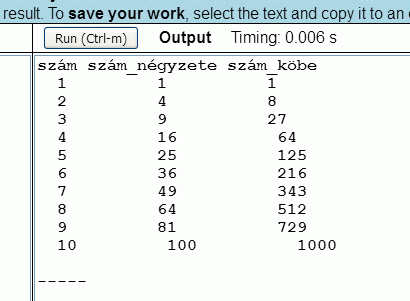
Vegyük azonban észre, hogy az előző feladat megoldásához képest a két- és háromjegyű számok megjelenése eltolja a kiírt számokat, így a táblázat (finoman szólva) nem lesz esztétikus. Ennek kiküszöbölésére egy újabb programozási eszközre lesz szükségünk.

elágazások

A korábbi, 16. programban azért nem tudtuk a négyzetszámokat és a köbszámokat egy táblázatban, esztétikusan elrendezni, mert a táblázat soraiban a számok pozícióját meghatározó szóközök száma független volt a megjelenített számjegyek számától. Például a 3. sorban jelenik meg először egy két számjegyből álló köbszám (27), amely egy szóközzel eltolja a köbszámok oszlopát. A 4. sorban pedig először jelenik meg egy két számjegyből álló négyzetszám (16), amely egy szóközzel eltolja a négyzetszámok oszlopát, és egy további szóközzel eltolja köbszámok oszlopát.

A megoldás az, hogy a szóközök számát a megjelenítendő számok számjegyeinek függvényében állapítsuk meg. Mivel a táblázat oszlopaiban az 'i', 'k1' és 'k2' nevű változók értékét íratjuk ki, a következő szerkezetet kellene megvalósítanunk a programban (feltéve, hogy 'i' esetében maximum 2 jegyű számokkal, 'k1' esetében maximum 3 jegyű számokkal, 'k1' esetében pedig maximum 4 jegyű számokkal dolgozunk):

ha i<10 akkor írassunk ki 3 db. szóközt,
egyébként írassunk ki 2 db. szóközt,
és ezután írassuk ki i-t;

ha k1<10 akkor írassunk ki 9 db. szóközt,
egyébként ha k1<100, akkor írassunk ki 8 db. szóközt,
egyébként írassuk ki 7 db. szóközt,
és ezután írassuk ki k1-t;

ha k2<10 akkor írassunk ki 10 db. szóközt,
egyébként ha k2<100, akkor írassunk ki 9 db. szóközt,
egyébként ha k2<1000, akkor írassunk ki 8 db. szóközt,
egyébként írassuk ki 7 db. szóközt,
és ezután írassuk ki k2-t.

A JavaScript programozási nyelv az if(...) {...} else {...}, ún. kétirányú elágazás szerkezetet biztosítja a fenti megoldásokhoz. Lássuk ezzel a szerkezettel megvalósítva a korábbi, 16. program javított változatát:

/* 17. program */
var k1,k2,n,s1,s2,s3;
n=10;

writeln("szám szám_négyzete szám_köbe");

for(var i=1;i<=n;i++) {
 k1=i*i;
 k2=k1*i;

 if(i<10) {
  s1="   "; // 3 db. szóköz
  }
 else {
  s1="  "; // 2 db. szóköz
  }

 if(k1<10) {
  s2="        "; // 8 db. szóköz
  }
 else if(k1<100) {
  s2="       "; // 7 db. szóköz
  }
 else {
  s2="      "; // 6 db. szóköz
  }

 if(k2<10) {
  s3="          "; // 10 db. szóköz
  }
 else if(k2<100) {
  s3="         "; // 9 db. szóköz
  }
 else if(k2<1000) {
  s3="        "; // 8 db. szóköz
  }
 else {
  s3="       "; // 7 db. szóköz
  }

 writeln(s1+i+s2+k1+s3+k2);
 }

writeln();
writeln("-----");

A programban használt új nyelvi elemek a következők:

• A programban feltüntettük az 's1', 's2' és 's3' változókban tárolt szóközök számát a // után megadott soron belüli megjegyzések megadásával (amelyeket a JavaScript interpreter figyelmen kívül hagy).
• Az < ("kisebb, mint") operátor segítségével két számot tudunk összehasonlítani. Az összehasonlítás eredménye vagy igaz (true), vagy hamis (false). Például 3<7 logikai értéke igaz; 8<2 logikai értéke pedig hamis.
• Az if(logikai_feltétel) {utasításblokk1} else {utasításblokk2} kétirányú elágazás működése:
  • az if(logikai_feltétel) fejrészben megadott logikai feltétel megvizsgálása (a logikai feltétel értéke vagy igaz, vagy hamis);
  • ha a logikai feltétel értéke igaz, az első utasításblokkban szereplő utasítások végrehajtása;
  • ha a logikai feltétel értéke hamis, a második utasításblokkban (az 'else' kulcsszó után következő utasításblokkban) szereplő utasítások végrehajtása.

A program képernyőképe a következő:

Az elágazások kiválóan felhasználhatóak olyan számsorozatok kiíratására, amelyek két részsorozatból állíthatóak elő. Tekintsük például az

sorozatot (i∈ℕ⁺). Vegyük észre, hogy az s_i sorozatot két részsorozat alkotja: az első részsorozat elemeit azok az s_i elemek alkotják, amelyekre 'i' páratlan, a második részsorozat elemeit pedig azok az s_i elemek alkotják, amelyekre 'i' páros szám. Ennek megfelelően a sorozat első 'n' elemét előállító program a következő:

/* 18. program */
var k,n;
k=1;
n=10; // legyen 'n' páros szám!

for(var i=1;i<=n;i++) {
 if(i%2==0) {
  k=i;
  }
 else {
  k=1/i;
  }
 writeln(i+". szám: "+k);
 }

writeln();
writeln("-----");

A programban két fontos JavaScript nyelvi elemet vezettünk be:

• két szám összehasonlítását az == operátorral tudjuk elvégezni (figyelem: az operátor két egyenlőségjelből áll!); az összehasonlítás eredménye egy logikai érték:
  • true (ha a két szám megegyezik, az összehasonlítás igaz logikai értéket ad)
  • false (ha a két szám nem egyezik meg, az összehasonlítás hamis logikai értéket ad)
• egy egész számot egy másik egész számmal elosztva az osztás maradékát a % operátorral állíthatjuk elő (maradékképzés; például az 5%2 művelet eredménye 1, a 8%3 művelet eredménye 2, a 10%5 művelet eredménye pedig 0)

Jegyezzük meg, hogy két szám összehasonlítására a JavaScript nyelvben használhatók a következő operátorok is: < (kisebb, mint; ld. 17. program), ≤, > (nagyobb, mint), ≥, és != (nem egyenlő).

Az előző, 18. programban az 'if' elágazó utasításban szereplő i%2==0 logikai feltétel arra szolgál, hogy eldöntsük, az 'i' egész szám osztható-e 2-vel (azaz páros-e). Általánosan megfogalmazva: ha meg akarjuk vizsgálni, hogy az 'i' egész szám osztható-e a 'j' egész számmal, az i%j==0 logikai feltételt kell megvizsgálnunk. Ha igaz, 'i' osztható 'j'-vel, ha hamis, nem osztható. Ezek után a JavaScript ciklusát és összehasonlító operátorait felhasználva egy egész számról el tudjuk dönteni, hogy prímszám-e vagy nem.

/* 19. program */
var p,k,n;
p=49; // vizsgálandó szám
k=0;
n=p;

for(var i=2;i<n;i++) {
 if(p%i==0) {
  k=i;
  break;
  }
 if(i*i>p) {
  break;  
  }
 }
if(k!=0) {
 writeln(k+" osztója a "+p+" számnak");
 writeln("a "+p+" szám nem prímszám");
 }
else {
 writeln("a "+p+" szám prímszám");
 }

writeln();
writeln("-----");

A program képernyőképe a következő:

A megoldás azon alapul, hogy egy 'p' számról úgy tudjuk eldönteni, hogy prímszám-e, hogy 2-től egészen (p-1)-ig egyenként megvizsgáljuk, hogy 'p'-nek van-e valódi (azaz nem triviális) osztója (lényegében ezen az elven alapul Erasztothenész szitája is). Érdemes megjegyeznünk, hogy 'p'>3 esetében nem szükséges egészen (p-1)-ig megvizsgálnunk a számokat, elegendő a vizsgálatot p négyzetgyökéig (√p-ig) folytatni. Például p=5 esetében 3-ra és 4-re már nem kell vizsgálnunk az oszthatóságot, mivel 3*3>5 teljesül.

A program működésének megértéséhez néhány fontos új programozási eszközt is meg kell tanulnunk:

• A programban szereplő 'for' ciklusban a ciklusváltozó kezdőértéke i=2, a ciklusfeltételben pedig i<n szerepel (és nem a korábbiakban szereplő i<=n).
• Ha a kétirányú elégazásban az 'else' kulcsszó utáni utasításblokk üres, az else {} ág elhagyható. Ebben az esetben egyirányú elágazásról beszélünk.
• A break; utasítás megszakítja a ciklus végrehajtását (azaz segítségével bármikor "kiléphetünk" a ciklusból).
• A 'k' változót arra használjuk, hogy segítségével a ciklus befejeződése után is el tudjuk dönteni, 'p' prímszám-e vagy nem (az ilyen funkcióval rendelkező változókat indikátorváltozóknak nevezzük). Mivel 'k' kezdőértéke k=0, és 'k' értékét csak abban az esetben változtatjuk meg, ha 'i' osztója 'p'-nek (ekkor az új érték k=i lesz, ahol p>i>0), a ciklusból való kilépés után elegendő 'k' értékét megvizsgálnunk:
  • ha k!=0, akkor 'p'-nek 'k' valós osztója, vagyis 'p' nem prímszám;
  • ha k==0, akkor 'p'-nek nincs valós osztója, vagyis 'p' prímszám.

Bizonyos esetekben egy ügyes trükkel kikerülhető az elágazás használata. Oldjuk meg például a következő feladatot kétféleképpen:

Feladat: írassuk ki a következő sorozat első 20 elemét (i∈ℕ⁺):

s_i = (−1)ⁱ*(2*i+3)

Először oldjuk meg a feladatot kétirányú elágazással:

/* 20. program, első változat */
var n;
n=10; 

for(var i=1;i<=n;i++) {
 if(i%2==0) {
  writeln(i+". szám: "+(2*i+3));
  }
 else {
  writeln(i+". szám: "+(-1)*(2*i+3));
  }
 }

writeln();
writeln("-----");

Ezután oldjuk meg az előző feladatot annak az ötletnek a felhasználásával, hogy ha egy változó (pl. "kit") értéke 1, akkor (−1)-gyel szorozva (−1) értéket kapunk, ha pedig ezt újra megszorozzuk (−1)-gyel, akkor a változó értéke ismét 1 lesz (és így tovább, minden szorzás után megváltozik a változó előjele):

/* 20. program, második változat */
var kit,n;
kit=-1;
n=10; 

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+kit*(2*i+3));
 kit=-1*kit;
 }

writeln();
writeln("-----");

A program képernyőképe a következő lesz:

Gyakorló feladatok:

(1) Írassa ki a következő sorozat első 15 elemét (i∈ℕ⁺):

(2) Írassa ki kétféleképpen a következő sorozat első 20 elemét (i∈ℕ⁺):

s_i = (−1)ⁱ⁺¹*(4*i²−10*i+5)

(3) Írassa ki kétféleképpen a következő sorozat első 10 elemét (i∈ℕ⁺):

s_i = (−1)ⁱ*(3*i−1)+(−1)⁽ⁱ⁺¹⁾*(i²−6*i)

(4) Írassa ki a következő sorozat első 10 értékét: {2, −6, 18, −54, ...}

(5) Írassa ki a következő sorozat első 20 értékét: {99, 1, 96, 4, 93, 7, ...}

függvények

Ha egy összetett képletet akarunk kiszámítani és akár többször is felhasználni egy programban, akkor készíthetünk egy olyan alprogramot, amely a képlet értékét kiszámítja, és bármikor fel tudjuk használni. Tegyük fel, hogy különböző sugarú körök kerületét és területét akarjuk kiíratni:

/* 21. program, első változat */
var r,dr,kerulet,terulet,n;
n=8; 

r=1;
dr=0.2;
for(var i=1;i<=n;i++) {
 kerulet=2*r*Math.PI;
 terulet=r*r*Math.PI;
 writeln("A kör sugara: "+r.toFixed(2));
 writeln("      kerülete: "+kerulet.toFixed(4));
 writeln("      területe: "+terulet.toFixed(4));
 r=r+dr;
 }

writeln();
writeln("-----");

A programban hivatkoztunk a π állandóra Math.PI módon. Mivel sokszor van szükségünk π értékére, a JavaScript nyelv ún. nevesített konstansként tartalmazza ennek az értékét. Egy másik nevezetes matematikai állandó az 'e' szám (2.71828...). A JavaScript nyelvben erre is bármikor hivatkozhatunk Math.E módon. Vegyük észre, hogy a nevesített konstansok két részből tevődnek össze: a Math osztálynévből és egy nagybetűs azonosítóból (pl. PI vagy E), amelyeket egy pont operátorral (.) kapcsolunk össze.

A program képernyőképe a következő lesz:

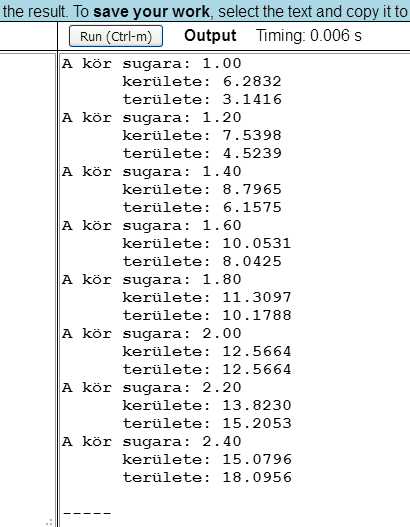
Most készítsük el az előző program egy módosított változatát úgy, hogy a kör kerületének és területének a kiszámítását két alprogram segítségével végezzük el. Az alprogramok közül a standard eljárásokról a 'writeln' eljárás kapcsán már beszéltünk. Most hozzunk létre két saját függvényt (function) 'kerulet' és 'terulet' néven:

/* 21. program, második változat */
function kerulet(r) {
 var k;
 k=2*r*Math.PI; 
 return k;
 }

function terulet(r) {
 var t;
 t=r*r*Math.PI; 
 return t;
 }

var r,dr,n;
n=8; 

r=1;
dr=0.2;
for(var i=1;i<=n;i++) {
 writeln("A kör sugara: "+r.toFixed(2));
 writeln("      kerülete: "+kerulet(r).toFixed(4));
 writeln("      területe: "+terulet(r).toFixed(4));
 r=r+dr;
 }

writeln();
writeln("-----");

Figyeljük meg, hogy a függvényeket megvalósító, kapcsos zárójelek között megadott {...} utasítások sokban hasonlítanak azokhoz a programokhoz, amelyeket eddig készítettünk. Létrehozhatunk bennük változókat (pl. var k;), ezekkel műveleteket végezhetünk, értékeket adhatunk nekik (pl. k=2*r*Math.PI;) stb. A függvényeknek mint alprogramoknak azonban egyedi jellemzőik is vannak. Emeljük ki a függvények legfontosabb ilyen jellemzőit:

1. Minden függvényt egyértelműen azonosít a függvény neve. A függvény meghatározása során a nevet közvetlenül a function azonosító ("kulcsszó") után adjuk meg. A név után mindig zárójelek állnak. Az előző programban a függvények nevei: kerület(...) és terület(...).
2. A függvény neve után szereplő zárójelek között egy vagy több változót adhatunk meg. A fenti programban például (r) módon egy 'r' nevű változót adtunk meg (egyes függvények esetében előfordulhat az az eset is, hogy nem adunk meg egy változót sem). A függvény neve után megadott változókat a függvény paramétereinek nevezzük. Az előző programban szereplő mindkét függvénynek egy paramétere van, az r változó.
   • A függvény neve és az utána szereplő zárójelek után kapcsos zárójelek ({...}) állnak. A kapcsos zárójelek között szerepelnek azok az utasítások, amelyeket a függvény meghívásakor a programnak végre kell hajtania. Ezekben az utasításokban (a függvény értékének a kiszámításakor) felhasználhatjuk a függvény paramétereit. Például a függvény kerületét a k=2*r*Math.PI; utasítással számolhatjuk ki és tárolhatjuk el a 'k' változóban.
3. A függvények meghatározásakor általában az utolsó utasítás a return, amely befejezi a függvény végrehajtását, és az utána megadott változó vagy kifejezés értékét hozzárendeli a függvény nevéhez (hasonló módon, mint amikor értéket adunk egy változónak). Például a return k; utasítás végrehajtása után a 'kerulet' függvény értéke a 'k' változóban tárolt érték lesz. Emeljük ki: a 'kerulet' függvény értéke az 'r' paraméter értékétől függ, a függvényt meghatározó képletnek (ill. az ezt megvalósító utasításoknak) megfelelően.
4. Ha szükségünk van a függvények értékére, az elkészített függvényeket a programban meghívhatjuk a függvény nevének, és (zárójelek között) a megfelelő paraméterértékeknek a megadásával. Például a fenti programban a 'kerület' függvényt a 'writeln' utasításban hívjuk meg writeln(...+kerulet(r).toFixed(4)); módon. A függvény meghívásakor megadott paraméterértékek a függvény paramétereinek mint változóknak értéket adnak, ezután a JavaScript interpreter végrehajtja a függvény utasításait, majd a 'return' utasításhoz érve értéket rendel a függvény nevéhez, és visszatér a függvényt meghívó utasításhoz.

Gyakorlásképpen írassuk ki néhány korábbi sorozat elemeit úgy, hogy létrehozunk egy 'sorozat' függvényt:

/* 22. program */

function sorozat(i) {
 var k;
/* k=i; // 8. program */
/* k=i*i; // 9. program */
 k=(1+i)/i; // 10. program
 return k;
 }

var n;
n=10;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+sorozat(i));
 }

writeln();
writeln("-----");

Figyeljük meg, hogy a különböző programok a 'sorozat' függvény egyszerű módosításával megvalósíthatók.

Gyakorló feladatok:

Oldja meg a ciklusok rész végén szereplő gyakorló feladatok közül az (1)-(4) feladatokat saját függvények létrehozásával!

A rekurzív módon megadott sorozatok elemei is kiszámíthatók függvények segítségével, mivel egy függvény saját magát is meghívhatja (ez ún. rekurzív függvényhívás). Ebben az esetben azonban nagyon óvatosan kell eljárnunk, mert ha nem megfelelően készítjük el a függvényeket, az könnyen végtelen hívásláncot eredményezhet. próbaképpen Írassuk ki 2 első 'n' hatványát ilyen módon (ezt korábban, a 11. programban már megoldottuk):

/* 23. program */
function sorozat(i) {
 if(i<=1) k=1;
 else k=sorozat(i-1)*2; 
 return k;
 }

var n;
n=20;

for(var i=1;i<=n;i++) {
 writeln(i+". szám: "+sorozat(i));
 }

writeln();
writeln("-----");

Nézzük meg a program működését akkor, ha meghívjuk a sorozat(3) függvényt. Ekkor

• ha 3==1 (ez most nem teljesül), akkor visszaadja az 1 értéket;
• ha 3>1 (ez most teljesül), akkor 2-vel megszorozza a sorozat előző, 2-dik elemét, amelyet úgy számít ki, hogy meghívja saját magát 2 értékkel. Ha azonban meghívjuk a sorozat(2) függvényt, akkor
  • ha 2==1 (ez most nem teljesül), akkor visszaadja az 1 értéket;
  • ha 2>1 (ez most is teljesül), akkor 2-vel megszorozza a sorozat előző, 1-dik elemét, amelyet úgy számít ki, hogy meghívja saját magát 1 értékkel. Ha azonban meghívjuk a sorozat(1) függvényt, akkor
    • ha 1==1 (ez most teljesül!), akkor visszaadja az 1 értéket és nem hívja meg többször önmagát;
    • ha 1>1 (ez most nem teljesül), akkor 2-vel megszorozza a sorozat előző, 0-dik elemét, amelyet úgy számít ki, hogy meghívja saját magát 0 értékkel stb. (szerencsére azonban idáig nem jutunk el).

A hívási lánc eredményeképpen tehát

sorozat(3)=2*sorozat(2)=2*(2*sorozat(1))=2*(2*(1))=4

adódik, ami pontosan megegyezik a sorozat 3-dik elemével (s₁=1, s₂=2¹=2 és s₃=2²=4). Nagyon fontos, hogy a hívási lánc befejeződését az garantálja, hogy i folyamatos csökkentésével előbb-utóbb eljutunk az (i==1) feltétel teljesüléséig, ami után a függvény visszaadja az 1 értéket (és nem hívja meg többször önmagát). Vagyis a 'sorozat' függvény helyes működését az

if(i<=1) k=1;
else ...

feltételes elágazó utasítás biztosítja.

Alkalmazások

Logikai igazságtáblázatok

A JavaScript logikai operátorai lehetővé teszik lényegében bármilyen logikai függvény (formula) kiszámítását. A legfontosabb logikai operátorok (feltéve, hogy 'p' és 'q' logikai típusú, azaz logikai értékeket tartalmazó változók):

• a=!p; (negáció, tagadás; "not")
• a=p && q; (konjunkció; "and")
• a=p || q; (diszjunkció; "or")

Ha logikai igaz (true) értékként az 1, logikai hamis (false) értékként a 0 értéket használjuk, ügyelnünk kell rá, hogy a JavaScript számára mindig egyértelmű legyen, hogy az 1 és 0 értékek számokat (Number) vagy logikai értékeket (Boolean) jelentenek.

Írassuk ki elsőként a konjunkció (∧) igazságtáblázatát!

// konjunkció igazságtáblázata (saját függvény létrehozásával)

function kon(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=a && b;
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"A∧B");
writeln("-------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var k=kon(i,j);
  writeln(i+" " +j+"  "+k);
  }
 }

writeln("-------");

A program képernyőképe a következő:

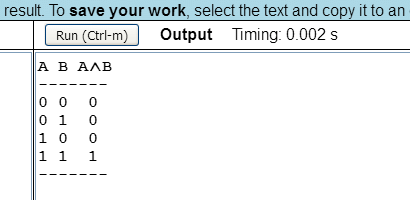
Az igazságtáblázatban szereplő A és B változók értékeit az 'i' és 'j' ciklusváltozók állítják elő. A 'kon' függvényben

• elsőként az 'i' és 'j' paraméterek átadott értékeit (1 vagy 0) logikai értékekké alakítjuk a Boolean standard függvény segítségével, és eltároljuk a logikai értékeket az 'a' és 'b' változókban;
• ezután kiszámítjuk az 'a' és 'b' változók mint logikai értékek (konstansok) konjunkcióját az && logikai operátor segítségével, és a konjunkció értékét eltároljuk a 'c' változóban;
• végül a 'c' változó értékét visszaalakítjuk számmá a Number standard függvény segítségével,, és hozzárendeljük a 'kon' függvény nevéhez (visszatérés után a 'kon' függvény értéke ez a szám lesz, amit az igazságtáblázat harmadik oszlopában kiíratunk).

Mivel a konjunkció igazságtáblázatát kiíró programban a 'kon' függvényt csak egyszer hívtuk meg, könnyen készíthető egy olyan program, amely saját függvény használata nélkül írja ki a konjunkció igazságtáblázatát.

// konjunkció igazságtáblázata (saját függvény használata nélkül)

writeln("A"+" " +"B"+" "+"A∧B");
writeln("-------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var a=Boolean(i), b=Boolean(j);
  var c=a && b;
  var k=Number(c);
  writeln(i+" " +j+"  "+k);
  }
 }

writeln("-------");

Jegyezzük meg, hogy a Boolean(...) függvény elhagyásával mindkét fenti program megfelelően fog működni, mert a logikai operátor (&&) használata egyértelművé teszi, hogy az 'i' és 'j' változók értékét logikai értéknek (vagyis nem számnak) tekintjük. A Number(...) függvényre azonban szükségünk van, ha biztosítani akarjuk, hogy a 'k' változó értékét, azaz az 1 (true) vagy 0 (false) logikai értékeket a JavaScript interpreter mindig számként írja ki.

Ezután írassuk ki a diszjunkció (∨) és a negáció (⌝) igazságtáblázatát!

// diszjunkció igazságtáblázata

function disz(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=a || b;
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"A∨B");
writeln("-------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var k=disz(i,j);
  writeln(i+" " +j+"  "+k);
  }
 }

writeln("-------");

A program képernyőképe a következő:

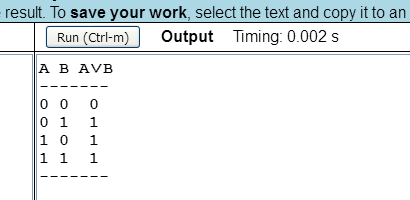
// negáció igazságtáblázata

function neg(x) {
 var a=Boolean(x);
 var c=!a;
 return Number(c);
 }

writeln("A"+" "+"A⌝B");
writeln("-----");

for(i=0;i<=1;i++) {
 var k=neg(i);
 writeln(i+"  "+k);
 }

writeln("-----");

A program képernyőképe a következő:

Írassuk ki gyakorlásként az implikáció (⊃) és az ekvivalencia (≡) igazságtáblázatát is!

// implikáció igazságtáblázata

function imp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!a || b;
 return Number(c);
 }

writeln("A"+" "+"B"+" "+"A⊃B");
writeln("-------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var k=imp(i,j);
  writeln(i+" " +j+"  "+k);
  }
 }

writeln("-------");

A program képernyőképe a következő:

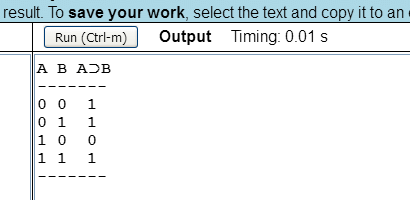
// ekvivalencia igazságtáblázata

function ekv(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=(a && b) || (!a && !b);
 return Number(c);
 }

writeln("A"+" "+"B"+" "+"A≡B");
writeln("-------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var k=ekv(i,j);
  writeln(i+" " +j+"  "+k);
  }
 }

writeln("-------");

A program képernyőképe a következő:

Végezetül határozzuk meg a C = A ∧ (A ⊃ B) ⊃. B formula igazságtáblázatát (modus ponens)!

// modus ponens

function mp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var p=!a || b; // (A ⊃ B) kiszámítása
 var q=a && p; // A ∧ (A ⊃ B) kiszámítása
 var c=!q || b;
 return Number(c);
 }

writeln("C = A ∧ (A ⊃ B) ⊃. B");
writeln();

writeln("A"+" "+"B"+" "+"C");
writeln("-----");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  var k=mp(i,j);
  writeln(i+" " +j+" "+k);
  }
 }

writeln("-----");

A program képernyőképe a következő:

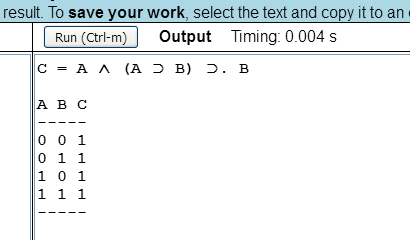
A program elkészítésekor felhasználtuk az implikációra vonatkozó A ⊃ B=⌝A ∨ B logikai azonosságot. Az igazságtáblázatból kiolvasható, hogy a modus ponens formula logikai törvény.

Gyakorló feladatok:

Írassa ki az összes fenti logikai művelet és formula igazságtáblázatát saját függvény használata nélkül is!

Kombinatorikai feladatok

A legalapvetőbb kombinatorikai műveletek a permutáció, a variáció és a kombináció. Elsőként állítsuk elő az (1,2,3,4) számok 3-ad osztályú ismétléses variációit, és számláljuk meg, hány ilyen variáció létezik.

/* ismétléses variációk, V4,3,i (1,2,3,4) */

var i,j,k;
var sorszam=0;

for(var i=1;i<=4;i++) {
 for(var j=1;j<=4;j++) {
  for(var k=1;k<=4;k++) {
   writeln("("+i+","+j+","+k+")");
   sorszam++;
   }
  }
 }
writeln();
writeln("a variációk száma: "+sorszam);

writeln("-----");

A program képernyőképe a következő:

...

Figyeljük meg, hogy a programban szereplő 'for' ciklusok száma megegyezik azzal, ahány elemet kiválasztunk a variációk előállítása során (3), és a 'for' ciklusok ciklusváltozói ('i', 'j' és 'k') azokat az értékeket veszik egymás után fel (1,2,3,4), amelyek közül a variációk előállítása során választhatunk.

A kiírt variációk megszámlálását úgy végezzük, hogy

• létrehozunk egy sorszam nevű változót,
• a sorszam változó kezdőértékét 0-ra állítjuk,
• minden új variáció kiírása után (writeln) a sorszam változó értékét eggyel növeljük.

Végül pedig ellenőrizzük, hogy a program által kiírt ismétléses variációk száma V₄^3,i=4³=64, megegyezik az ismétléses variációk számát megadó képlet által szolgáltatott értékkel.

Ezután állítsuk elő az (1,2,3,4) számok 3-ad osztályú ismétlés nélküli variációit, és számláljuk meg, hány ilyen variáció létezik.

/* ismétlés nélküli variációk, V4,3 (1,2,3,4) */
/* első változat */

var i,j,k;
var sorszam=0;

for(var i=1;i<=4;i++) {
 for(var j=1;j<=4;j++) {
  if(j!=i) {
   for(var k=1;k<=4;k++) {
    if(k!=i && k!=j) {
     writeln("("+i+","+j+","+k+")");
     sorszam++;
     } // második if(...) blokk vége
    }
   } // első if(...) blokk vége
  }
 }
writeln();
writeln("a variációk száma: "+sorszam);

writeln("-----");

A program hasonlóan működik az előző programhoz, amely az (1,2,3,4) számok ismétléses variációit állította elő. Azonban most csak azokat a variációkat íratjuk ki, amelyekben

• az 'i' és a 'j' változók értéke nem egyezik meg (első 'if' elágazó utasítás), és
• sem az 'i' és a 'k' változók, sem a 'j' és a 'k' változók értéke nem egyezik meg (második 'if' elágazó utasítás).

Így tudjuk biztosítani, hogy a kiírt variációkban nincsenek azonos (ismétlődő) értékek.

A program egyszerűsíthető a continue; utasítás használatával, amelyet egy ciklusban használva a JavaScript interpreter kihagyja ("átugorja") a ciklusmag további utasításait. De ezzel legyünk nagyon óvatosak: ha olyan 'while' ciklust használunk, amelyben a ciklusmag utolsó utasítása a ciklusváltozó növelése (pl. i=i+1; módon), akkor a continue; utasítás könnyen végtelen ciklushoz vezethet!

/* ismétlés nélküli variációk, V4,3 (1,2,3,4) */
/* második változat */

var i,j,k;
var sorszam=0;

for(var i=1;i<=4;i++) {
 for(var j=1;j<=4;j++) {
  if(j==i) continue;
  for(var k=1;k<=4;k++) {
   if(k==i || k==j) continue;
   writeln("("+i+","+j+","+k+")");
   sorszam++;
   }
  }
 }
writeln();
writeln("a variációk száma: "+sorszam);

writeln("-----");

A programban a continue; utasítás használatával kihagyjuk ("kiszitáljuk") azokat a variációkat, amelyekben

• az 'i' és a 'j' változók értéke megegyezik (első 'if' elágazó utasítás), vagy
• az 'i' és a 'k' változók vagy a 'j' és a 'k' változók értéke megegyezik (második 'if' elágazó utasítás).

A program képernyőképe a következő:

Végül ellenőrizzük, hogy a program által kiírt ismétlés nélküli variációk száma V₄³=4!/(4-3)!=(4*3*2*1)/(1)=24 megegyezik az ismétlés nélküli variációk számát megadó képlet által szolgáltatott értékkel.

Mivel az ismétlés nélküli permutációk az ismétlés nélküli variációk speciális esetei (ha n=k, akkor V_nⁿ=P_n), ezért a fenti program segítségével könnyen előállíthatók az (1,2,3) számok ismétlés nélküli permutációi.

/* ismétlés nélküli permutációk, P3 (1,2,3) */

var i,j,k;
var sorszam=0;

for(var i=1;i<=3;i++) {
 for(var j=1;j<=3;j++) {
  if(j==i) continue;
  for(var k=1;k<=3;k++) {
   if(k==i || k==j) continue;
   writeln("("+i+","+j+","+k+")");
   sorszam++;
   }
  }
 }
writeln();
writeln("a variációk száma: "+sorszam);

writeln("-----");

Az egyetlen különbség az előző programhoz képest, hogy a 'for' ciklusokban a ciklusváltozók értéke csak az (1,2,3) értékeket veheti fel.

A program képernyőképe a következő:

Végül ellenőrizzük, hogy a program által kiírt ismétlés nélküli variációk száma P₃=3!=(3*2*1)=6 megegyezik az ismétlés nélküli permutációk számát megadó képlet által szolgáltatott értékkel.

Emlékezzünk vissza, hogy a fenti feladat (három elem ismétlés nélküli permutációja) korábban már előfordult, amikor három keresztnév különböző permutációit kellett kiíratnunk. Most oldjuk meg a feladatot úgy, hogy az 1, 2 és 3 számok ismétlés nélküli permutációit előállító programot használjuk fel:

/* ismétlés nélküli permutációk, P3 (T,F,K) */

var i,j,k;
var nev=["???","Tercsi","Fercsi","Kata"]; // tömb
var sorszam=0;

for(var i=1;i<=3;i++) {
 for(var j=1;j<=3;j++) {
  if(j==i) {
   continue;
   }
  for(var k=1;k<=3;k++) {
   if(k==i || k==j) {
    continue;
    }
   writeln("["+nev[i]+","+
               nev[j]+","+
               nev[k]+"]");
   sorszam++;
   } 
  }
 }
writeln();
writeln("a permutációk száma: "+sorszam);

writeln("_____________");

A fenti program legfontosabb eleme a 'nev' változó, amely egy olyan tömb, amely a permutálandó keresztneveket tartalmazza. A 'nev' tömb egyes elemeire az elemek sorszámával tudunk hivatkozni (pl. nev[1] értéke "Tercsi" stb.). Mivel a tömbelemek sorszáma (a karakterláncokhoz teljesen hasonlóan) 0-val kezdődik, az egyszerűség kedvéért a tömb 0-dik elemének a "???" értéket adtuk (jelezve ezzel, hogy a 0-dik elemet most nem használjuk fel). Így az előző programot minimális változtatással át tudtuk alakítani úgy, hogy az 1, 2 és 3 számok helyett a keresztnevek permutációit írassa ki, azaz a nev[1], nev[2] és nev[3] tömbelemekben tárolt keresztneveket. Mivel a programban a 'nev' tömb 0-dik elemére nem hivatkozunk, a "???" érték nem okoz semmilyen problémát (azaz ide akármilyen keresztnevet is beírhattunk volna).

A keresztnevek permutációit kiíró program természetesen megvalósítható a 'continue' utasítás nélkül is:

// keresztnevek permutációinak kiírása 2.0 verzió

var i,j,k;
var nev=["???","Tercsi","Fercsi","Kata"]; // tömb
var sorszam=0;

for(var i=1;i<=3;i++) {
 for(var j=1;j<=3;j++) {
  if(j!=i) {
   for(var k=1;k<=3;k++) {
    if(k!=i && k!=j) {
     writeln("["+nev[i]+","+nev[j]+","+nev[k]+"]");
     sorszam++;
     } // második if(...) blokk vége
    }
   } // első if(...) blokk vége
  }
 }
writeln();
writeln("a permutációk száma: "+sorszam);

writeln("_____________");

Végül jegyezzük meg, hogy a keresztnevek permutációit kiíró program megvalósítható tömbök használata nélkül is:

// keresztnevek permutációinak kiírása 3.0 verzió

function nev(n) {
 var s="???";
 switch(n) {
  case 1: s="Tercsi"; break;
  case 2: s="Fercsi"; break;
  case 3: s="Klára"; break;
  }
 return s;
 }

var i,j,k;
var sorszam=0;

for(var i=1;i<=3;i++) {
 for(var j=1;j<=3;j++) {
  if(j!=i) {
   for(var k=1;k<=3;k++) {
    if(k!=i && k!=j) {
     writeln("["+nev(i)+","+
             nev(j)+","+nev(k)+"]");
     sorszam++;
     } // második if(...) blokk vége
    }
   } // első if(...) blokk vége
  }
 }
writeln();
writeln("a permutációk száma: "+sorszam);

writeln("_____________");

Ezután állítsuk elő az (1,2,3,4) számok 3-ad osztályú ismétlés nélküli kombinációit, és számláljuk meg, hány ilyen kombináció létezik.

/* ismétlés nélküli kombinációk, C4,3 (1,2,3,4) */

var i,j,k;
var sorszam=0;

for(var i=1;i<=4;i++) {
 for(var j=i+1;j<=4;j++) {
  for(var k=j+1;k<=4;k++) {
   writeln("{"+i+","+j+","+k+"}");
   sorszam++;
   }
  }
 }
writeln();
writeln("a kombinációk száma: "+sorszam);

writeln("-----");

A program képernyőképe a következő:

A program azon az elven működik, hogy mivel a kombinációk esetében a kiválasztott elemek sorrendje nem számít (halmazokat állítunk elő), a kiválasztott elemeket tetszőlegesen, például növekvő sorrendben elrendezhetjük. Ez a program szempontjából azt jelenti, hogy az egymásba ágyazott 'for' ciklusok 'i', 'j' és 'k' ciklusváltozóira az i<j<k feltételnek kell teljesülnie (vegyük észre, hogy egy kombinációt {i,j,k} módon állítunk elő!). Ha a 'j' ciklusváltozó kezdőértéke i+1, a 'k' ciklusváltozó kezdőértéke pedig j+1, akkor a fenti feltétel nyilvánvalóan teljesül.

Végül ellenőrizzük, hogy a program által kiírt ismétlés nélküli kombinációk száma C₄³=4!/(3!*(4-3)!)=(4*3*2*1)/(3*2*1)=4 megegyezik az ismétlés nélküli kombinációk számát megadó képlet által szolgáltatott értékkel.

Az előző program ismeretében könnyen elő tudjuk állítani az (1,2,3,4) számok 3-ad osztályú ismétléses kombinációit. Számláljuk meg most is, hány ilyen kombináció létezik.

/* ismétléses kombinációk, C4,3,i (1,2,3,4) */

var i,j,k;
var sorszam=0;

for(var i=1;i<=4;i++) {
 for(var j=i;j<=4;j++) {
  for(var k=j;k<=4;k++) {
   writeln("{"+i+","+j+","+k+"}");
   sorszam++;
   }
  }
 }
writeln();
writeln("a kombinációk száma: "+sorszam);

writeln("-----");

A program képernyőképe a következő:

A program abban különbözik az előző programtól, hogy most megengedjük, hogy a ciklusváltozók értéke megegyezzen. Azaz most az egymásba ágyazott 'for' ciklusok 'i', 'j' és 'k' ciklusváltozóira az i≤j≤k feltételnek kell teljesülnie. Ennek megfelelően

• a 'j' ciklusváltozó kezdőértéke most i (azaz 'j' nem lehet kisebb, mint 'i'),
• a 'k' ciklusváltozó kezdőértéke pedig j (azaz 'k' nem lehet kisebb, mint 'j'),

vagyis a ciklusváltozók kezdőértékének beállítása biztosítja, hogy a fenti feltétel teljesüljön.

Végül ellenőrizzük, hogy a program által kiírt ismétlés nélküli kombinációk száma

C₄^3,i=(4+3-1)!/(3!*(4+3-1-3)!)=(6*5*4*3*2*1)/((3*2*1)*(3*2*1))=(6*5*4)/(3*2*1)=(2*5*2)=20

megegyezik az ismétléses kombinációk számát megadó képlet által szolgáltatott értékkel.

Végül jegyezzük meg, hogy az ismétléses permutációk szintén előállíthatóak lennének egy megfelelő JavaScript program segítségével, azonban ezzel most nem foglalkozunk.

Gyakorló feladatok:

(ismétléses variációk)

(1.1) Írassa ki az (1,2,3,4,5) számok 3-ad osztályú ismétléses variációit, és ellenőrizze az eredményt!

(1.2) Írassa ki az (1,2,3,4,5) számok 2-ad osztályú ismétléses variációit, és ellenőrizze az eredményt!

(1.3) Írassa ki az (1,2,3,4) számok 2-ad osztályú ismétléses variációit, és ellenőrizze az eredményt!

(1.4) Írassa ki az (1,2,3) számok 2-ad osztályú ismétléses variációit, és ellenőrizze az eredményt!

(ismétlés nélküli variációk)

(2.1) Írassa ki az (1,2,3,4,5) számok 3-ad osztályú ismétlés nélküli variációit, és ellenőrizze az eredményt!

(2.2) Írassa ki az (1,2,3,4,5) számok 2-ad osztályú ismétlés nélküli variációit, és ellenőrizze az eredményt!

(2.3) Írassa ki az (1,2,3,4) számok 2-ad osztályú ismétlés nélküli variációit, és ellenőrizze az eredményt!

(2.4) Írassa ki az (1,2,3) számok 2-ad osztályú ismétlés nélküli variációit, és ellenőrizze az eredményt!

(ismétlés nélküli permutációk)

(3.1) Írassa ki az (1,2) számok ismétlés nélküli permutációit!

(3.2) Szorgalmi feladat: írassa ki az (1,2,3,4) számok ismétlés nélküli permutációit!

(ismétlés nélküli kombinációk)

(4.1) Írassa ki az (1,2,3,4,5) számok 3-ad osztályú ismétlés nélküli kombinációit, és ellenőrizze az eredményt!

(4.2) Írassa ki az (1,2,3,4,5) számok 2-ad osztályú ismétlés nélküli kombinációit, és ellenőrizze az eredményt!

(4.3) Írassa ki az (1,2,3,4) számok 2-ad osztályú ismétlés nélküli kombinációit, és ellenőrizze az eredményt!

(4.4) Írassa ki az (1,2,3) számok 2-ad osztályú ismétlés nélküli kombinációit, és ellenőrizze az eredményt!

(ismétléses kombinációk)

(5.1) Írassa ki az (1,2,3,4,5) számok 3-ad osztályú ismétléses kombinációit, és ellenőrizze az eredményt!

(5.2) Írassa ki az (1,2,3,4,5) számok 2-ad osztályú ismétléses kombinációit, és ellenőrizze az eredményt!

(5.3) Írassa ki az (1,2,3,4) számok 2-ad osztályú ismétléses kombinációit, és ellenőrizze az eredményt!

(5.4) Írassa ki az (1,2,3) számok 2-ad osztályú ismétléses kombinációit, és ellenőrizze az eredményt!

Egyéb alkalmazások

A programozás kiválóan alkalmazható különböző matematikai feladatok megoldására és a kapott eredmények szemléltetésére. Korábban már volt szó a számsorozatokról. Először ismerjünk meg néhány egyszerű, a számok kiválasztásával (kiválogatásával) kapcsolatos feladatot, majd néhány számelméleti feladat számítógépes megoldását.

I. sorozatelemek kiválogatása

Korábban (a ciklusok megismerésekor) megtanultuk, hogyan lehet az első 'n' természetes számot kiírni. Ez megfelel annak, hogy kiíratjuk az

s_i=i (i∈ℕ⁺)

sorozat első 'n' elemét. Ez a sorozat megadható rekurzív módon is

s₁=1, s_i+1=s_i+1 (i∈ℕ⁺)

formában. Ha a sorozat elemeit a 'k' változóban állítjuk elő, a sorozat első 'n' elemét az alábbi program írja ki:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 writeln(k);
 k=k+1;
 }

writeln();
writeln("-----");

Az alábbiakban a következő feladattípusra adunk példákat:

• állítsuk elő egy rekurzív módon megadott sorozat elemeit;
• egy adott feltétel alapján válogassuk ki a feltételnek megfelelő sorozatelemeket.

Jegyezzük meg, hogy mindegyik példa a népszerű "gondoltam egy számot" feladattípus egy variációja. Nem túl sok természetes számot választva ez a feladattípus kiválóan felhasználható az általános iskola alsóbb évfolyamain is. A természetes számokat például úgy lehet megválasztani, hogy egy adott kiválasztási feltétel

• pontosan egy megoldást adjon;
• legalább egy megoldást adjon;
• ne legyen megoldás;
• stb.

A fenti lehetőségek természetesen tetszőlegesen variálhatóak a különböző kiválasztási feltételekkel.

Első példaként válogassuk ki az első 'n' természetes szám közül a páros számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%2==0) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Második példaként válogassuk ki az első 'n' természetes szám közül a hárommal osztható számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%3==0) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Harmadik példaként válogassuk ki az első 'n' természetes szám közül a hárommal osztható páros számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%3==0 && k%2==0) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Vegyük észre, hogy a két kiválasztási feltételt (k%3==0 és k%2==0) az 'és' logikai művelettel (&&) kapcsoltuk össze.

Negyedik példaként válogassuk ki az első 'n' természetes szám közül a hárommal osztható vagy az öttel osztható számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%3==0 || k%5==0) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Vegyük észre, hogy a két kiválasztási feltételt (k%3==0 és k%5==0) most a 'vagy' logikai művelettel (||) kapcsoltuk össze.

Ötödik példaként válogassuk ki az első 'n' természetes szám közül a kettővel osztható (azaz páros) és hárommal nem osztható számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%2==0 && k%3!=0) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Egy nagyon fontos megjegyzés: ha a fenti programban a hárommal nem osztható számokat negációval akarjuk kiválogatni, akkor nagyon fontos, hogy a tagadott logikai kifejezést zárójelbe tegyük:

...
for(var i=1;i<=n;i++) {
 if(k%2==0 && !(k%3==0)) {
  writeln(k);
  }
 k=k+1;
 }
...

Hatodik példaként válogassuk ki az első 'n' természetes szám közül a hárommal osztva 1 maradékot adó, de nem páros és héttel nem osztható számokat:

var k,n;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%3==1 && !(k%2==0 || k%7==0)) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Vegyük észre, hogy a szűkítő feltételt ("nem" k%2==0 és "nem" k%7==0) a 'vagy' logikai művelettel (||) kapcsoltuk össze és az egész kifejezést tagadtuk vagy "negáltuk" (!). A programban követett megoldás (!(k%2==0 || k%7==0)) helyett a fenti feladat szűkítő feltétele a de Morgan logikai azonosság alapján

k%2!=0 && k%7!=0

módon is megadható (jegyezzük meg, hogy a negáció használatára vonatkozó korábbi megjegyzésnek megfelelően k%2!=0 és !(k%2==0) ekvivalens kifejezések).

Hetedik példaként ("haladó feladatként") adjunk meg olyan kiválasztási feltételt, amelynek az első 100 természetes szám közül pontosan egy szám felel meg. Például legyen a keresett szám olyan, amely

• hárommal osztva egy maradékot ad,
• néggyel osztva három maradékot ad, és
• héttel osztva kettő maradékot ad.

var k,n;
k=1;
n=100;

for(var i=1;i<=n;i++) {
 if(k%3==1 && k%7==2 && k%4==3) {
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Nyolcadik példaként ("versenyfeladatként") adjunk meg olyan kiválasztási feltételt, amelynek az első 1000 természetes szám közül pontosan egy szám felel meg. Egy lehetséges megoldás: legyen a keresett szám olyan, amely

• öttel osztható,
• kilenccel osztható, és
• 13-mal osztható.

var k,n;
k=1;
n=1000;

for(var i=1;i<=n;i++) {
 if(k%5==0 && k%9==0 && k%13==0){
  writeln(k);
  }
 k=k+1;
 }

writeln();
writeln("-----");

Az előző programok végtelen sok variációját kapjuk, ha az első 'n' természetes számot előállító sorozat helyett más sorozatot választunk. Például válasszuk az

s₁=1
s₂=1
s_i=s_i−1+s_i−2 (i∈ℕ, i>2)

Fibonacci-sorozatot. (A sorozat elemeit korábban már előállítottuk, most egy másik módszert mutatunk meg.) A Fibonacci-sorozat első 'n' elemét előállító program:

// Fibonacci-sorozat előállítása

var k2,k1,k,n;
k2=0;
k1=0;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 writeln(k);
 k2=k1;
 k1=k; 
 k=k1+k2;
 }

writeln();
writeln("-----");

A program működésének lényege, hogy

• az i-ik sorozatelemet a 'k' változó tárolja,
• az (i−1)-ik (a megelőző) sorozatelemet a 'k1' változó tárolja,
• az (i−2)-ik (a megelőzőt megelőző) sorozatelemet a 'k2' változó tárolja.

A működés során minden lépésben először kiíratjuk 'k' értékét (az aktuális sorozatelemet), majd a 'k2' változóban eltároljuk a 'k1' változó értékét, a 'k1' változóban eltároljuk a 'k' értékét, és kiszámítjuk a következő sorozatelem értékét (k=k1+k2;).

A három változó értéke a a program végrehajtása során a következőképpen változik:

Ezek után írassuk ki például a Fibonacci-sorozat hárommal osztható elemeit!

var k2,k1,k,n;
k2=0;
k1=0;
k=1;
n=10;

for(var i=1;i<=n;i++) {
 if(k%3==0) {
  writeln(k);
  }
 k2=k1;
 k1=k; 
 k=k1+k2;
 }

writeln();
writeln("-----");

Gyakorló feladatok:

Készítsünk programokat az összes eddig megismert sorozatból, amelyek a sorozat első 'n' eleméből adott feltételek szerint kiválogatják a feltételeknek megfelelő elemeket!

II. aritmetika, számelmélet

Az eddig megtanult JavaScript eszközökkel könnyen tudunk táblázatokat is készíteni. Például írassuk ki a szorzótáblát:

// szórzótábla

var i=1;
var n=9;

write("   | ");
while(i<=n) {
 write("0"+i+" ");
 i=i+1;
 }
writeln();

writeln("-------------------------------");

var s=1;
while(s<=n) {

write("0"+s);

i=1;
write(" | ");
while(i<=n) {
 if(s*i<10) {
  write("0"+s*i+" ");
  }
 else {
  write(s*i+" ");
  }
 i=i+1;
 }
writeln();

s=s+1;
}

writeln("_____________");

A program képernyőképe a következő:

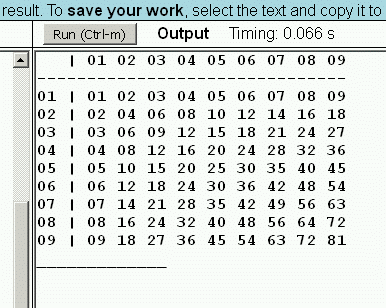
Ezek után oldjunk meg néhány számelméleti feladatot. Például írassuk ki az első 25 természetes szám közül a primszámokat!

/* primszámok kiírása */
var n=25;

for(var i=2;i<=n;i++) {
 var prim=true;
 for(var j=2;j<i;j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   writeln(i+" nem prim, "+j+" osztoja");
   prim=false;
   break;
   }
  }
 if(prim) {
  writeln(i);
  }
 }

writeln();
writeln("-----");

A program képernyőképe a következő:

A program működése a következő:

• Beállítjuk az 'n' változóban, hány számot vizsgáljunk.
• Az első 'for' ciklus 'i' ciklusváltozója végigmegy a természetes számokon 2-től 'n'-ig (az 1 nem primszám!). A ciklusmagban először egy 'prim' nevű logikai változót 'true' (igaz) értékre állítunk: ez fogja számunkra jelezni, hogy az 'i' változó aktuális értéke primszám-e.
• A második 'for' ciklus 'j' ciklusváltozója végigmegy a természetes számokon 2-től (j=2) 'i−1'-ig (j<i). Ha 'i'-nek van valódi osztója, akkor az csak ezek közül a számok közül kerülhet ki. A ciklusban minden lépésben megvizsgáljuk, hogy 'j' valódi osztója-e 'i'-nek?
  • Elosztjuk 'i'-t 'j'-vel, és az eredményt a 'q' változóban tároljuk.
  • 'j' akkor valódi osztó, ha 'q' egész részét megszorozva 'j'-vel visszakapjuk 'i'-t ('q' egész részét Math.trunc(q) adja meg úgy, hogy levágja a tizedesjegyeket). Ha tehát a Math.trunc(q)*j==i logikai kifejezés igaz, akkor
    • a 'prim' változót 'false'-ra (hamis) állítjuk, mert 'i'-nek megtaláltuk egy valódi osztóját, vagyis 'i' nem prim;
    • kiíratjuk az 'i' értéke mellett a 'j' valódi osztó értékét;
    • 'break' utasítással kilépünk a második 'for' ciklusból.
• A második ciklus lefutása után megvizsgáljuk a 'prim' logikai változó értékét. Ha 'prim' értéke igaz (true), akkor kiírjuk 'i' értékét. Jegyezzük meg, hogy mivel a 'prim' logikai változó megadja, hogy az 'i' változó prímszám-e, a kiíratás történhet a 'for' cikluson kívül is.

Megjegyzések:
– A második 'for' ciklusban elég lenne ha a 'j' ciklusváltozó 2-től az 'i' négyzetgyökéig keresné 'i' valódi osztóit. Az 'i' változó értékének négyzetgyökét a JavaScript nyelvben Math.sqrt(i) adja meg.
– Azt, hogy a 'j' szám osztója-e az 'i' számnak, a JavaScript '%' operátorával is megvizsgálhatjuk. Mivel i%j megadja, hogy az 'i' egész számot a 'j' egész számmal osztva mennyi az osztási maradék, az i%j==0 logikai kifejezés pontosan akkor igaz, ha 'j' osztója 'i'-nek.

Az előző program egy másik megvalósítása a fentieknek megfelelően:

/* primszámok kiírása */
var n=25;

var i=2;
while(i<=n) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  if(i%j==0) {
   prim=false;
   break;
   }
  }
 if(prim) {
  writeln(i);
  }
 else {
  writeln(i+" nem prim ("+j+" oszto)");
  }
 i=i+1;
 }

writeln();
writeln("__________________");

Alakítsuk át az előző programot úgy, hogy csak a primszámokat írja ki, és végül írassuk ki azt is, hány primszámot találtunk. (A programban az új sorokat sárgával kiemeltük.)

/* primszámok kiírása */

var n=25;
var sum=0;

for(var i=2;i<=n;i++) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   prim=false;
   break;
   }
  }
 if(prim) {
  writeln(i);
  sum++;
  }
 else {
  }
 }

writeln();
writeln(n+"-nel nem nagyobb primszámok száma: "+sum);

writeln();
writeln("-----");

Készítsük el az előző programot egy prim(x) függvény segítségével, amely 'igaz' (true) értéket ad vissza, ha 'x' primszám, és 'hamis' (false) értéket, ha 'x' nem primszám:

/* primszámok kiírása */

function prim(x) { 
 var p=true;
 for(var j=2;j<x;j++) {
  if(x%j==0) {
   p=false;
   break;
   }
  }
 return p;
 }

var n=100;
var sum=0;

for(var i=2;i<=n;i++) {
 if(prim(i)) {
  writeln(i);
  sum=sum+1;
  }
 }

writeln();
writeln("Az első "+n+" természetes szám között "+
        "összesen "+sum+" darab primszám van.");

writeln();
writeln("-----");

A korábbi programok alapján könnyű egy olyan programot készíteni, amely egy tetszőleges számról (például 11-ről) eldönti, hogy primszám-e.

/* primtulajdonság vizsgálata */

var i=11; // feltétel: i>1

var prim=true;
for(var j=2;j<=Math.sqrt(i);j++) {
 var q=i/j;
 if(Math.trunc(q)*j==i) {
  prim=false;
  break;
  }
 }
if(prim) {
 writeln(i+" primszam");
 }
else {
 writeln(i+" nem primszam");
 }

writeln();
writeln("-----");

A fenti programot ismét alakítsuk át úgy, hogy egy függvény vizsgálja meg, hogy egy adott szám (pl. 21) prim-e:

/* primtulajdonság vizsgálata */

function primszam(i) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   prim=false;
   break;
   }
  }
 return prim;
 }

var i=21; // feltétel: i>1

if(primszam(i)) {
 writeln(i+" primszam");
 }
else {
 writeln(i+" nem primszam");
 }

writeln();
writeln("-----");

Fontos megjegyeznünk, hogy a primszam(i) függvény csak egynél nagyobb természetes számok (i>1) esetén működik megfelelően. Ahhoz, hogy pl. i<=1 esetén is jól működjön, kellene pl. egy

   function primszam(i) {
    if(i<=1) return false;
    ...

kivételkezelő utasítás a függvény definíciójának (deklarációjának) elején. Ha negatív számokra is fel akarjuk készíteni a függvényt, akkor pl. a következő utasításokra lenne szükség (szintén a deklaráció elején):

   function primszam(i) {
    i=Math.abs(i);
    if(i<=1) return false;
    ...

Az előző függvény egy variációjával készítsük el Erasztothenész szitáját (azaz "szitáljuk ki" azokat a számokat, amelyek nem primszámok):

// Erasztothenész szitája

function prim(x) { 
/* feltételezzük hogy 'x' pozitív természetes szám */
 var p;
 if(x<=1) {
  p=false;
  }
 else {
  p=true;
  for(var j=2;j<=Math.sqrt(x);j++) {
   if(x%j==0) {
    p=false;
    break;
    }
   }
  }
 return p;
 }

var i=1, j=1, k=1;

i=1;
while(i<=10) {
 j=1;
 while(j<=10) {
  if(prim(k)) { // 'k' primszám
   if(k<10) { // 'k' egy számjegyű
    write("0"+k+" "); // "vezető" 0
    }
   else { // 'k' két számjegyű
    write(k+" ");
    }
   }
  else { // 'k' nem primszám
   write("   ")
   }
  k=k+1;
  j=j+1;
  } // sor vége
 writeln();
 i=i+1;
 } // táblázat vége

writeln("_____________");

Erasztothenész szitáját úgy is kiírathatjuk, hogy a primszámok után egy csillagot (*) teszünk:

// Erasztothenész szitája 2.0 verzió

function prim(x) { 
/* feltételezzük hogy 'x' pozitív természetes szám */
 var p;
 if(x<=1) {
  p=false;
  }
 else {
  p=true;
  for(var j=2;j<=Math.sqrt(x);j++) {
   if(x%j==0) {
    p=false;
    break;
    }
   }
  }
 return p;
 }

var i=1, j=1, k=1;
var s=0;

i=1;
while(i<=10) {
 j=1;
 while(j<=10) {
  if(prim(k)) {
   if(k<10) {
    write("0"+k+"* ");
    }
   else {
    write(k+"* ");
    }
   s=s+1;
   }
  else { // 'k' nem prim
   if(k<10) {
    write("0"+k+"  ");
    }
   else {
    write(k+"  ");
    }
   }
  k=k+1;
  j=j+1;
  }
 writeln();
 i=i+1;
 }

writeln();
writeln("primszámok száma: "+s);

writeln("_____________");

A program képernyőképe a következő:

Az előző programok alapján nagyon könnyen készíthetünk egy olyan programot, amely egy adott természetes szám (pl. 25) osztóit írja ki:

/* egy szám osztói */

var n=25;

for(var j=1;j<=n;j++) {
 var q=n/j;
 if(Math.trunc(q)*j==n) {
  writeln(n+" osztoja "+j);
  }
 }

writeln();
writeln("-----");

A program képernyőképe a következő:

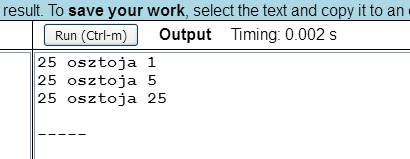
Az előző két program kombinálásával pedig kiírathatjuk egy szám (pl. 225) primosztóit:

/* egy szám primosztói */

function primszam(i) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   prim=false;
   break;
   }
  }
 return prim;
 }

var n=225;

for(var j=2;j<=n;j++) {
 var q=n/j;
 if(Math.trunc(q)*j==n && primszam(j)) {
  writeln(n+" primosztoja "+j);
  }
 }

writeln();
writeln("-----");

Vegyük észre, hogy az osztók közül úgy válogattuk ki a primszámokat, hogy a primszam(j) függvényt a logikai "és" (&&) művelettel kapcsoltuk hozzá az 'n' osztóit kiválasztó logikai feltételhez (Math.trunc(q)*j==n).

Innentől már csak egy lépés, hogy egy tetszőleges természetes szám (pl. 2250) primtényezőit meghatározzuk:

/* egy szám összes primosztója */

function primszam(i) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   prim=false;
   break;
   }
  }
 return prim;
 }

var n=2450;
var m=n;

cikl: 
for(var j=2;j<=n;j++) {
 for(var k=1;k<=n;k++) {
  var q=m/j;
  if(Math.trunc(q)*j==m && primszam(j)) {
   writeln(n+" primosztoja "+j);
   m=q;
   if(m==1) break cikl;
   }
  else {
   break;
   }
  }
 }

writeln();
writeln("-----");

A program képernyőképe a következő:

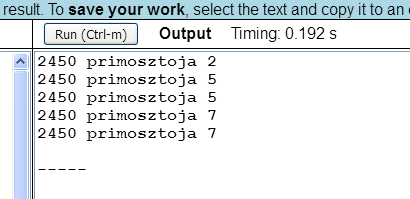
A program a következő pontokban különbözik az előző programtól:

• Egy 'm' változóban eltároljuk azt a számot ('n'), amelynek a primtényezőit meg akarjuk határozni.
• Azt a 'for' ciklust, amely az 'n' változóban tárolt szám lehetséges osztóit állítja elő a 'j' ciklusváltozóban, megjelöljük egy 'cikl' azonosítóval ("címkével").
• Létrehozunk egy új 'for' ciklust, amelynek a 'k' ciklusváltozója az 'n' szám primosztóinak a hatványkitevőit számlálja meg az 'n' primtényezős alakjában (pl. 25 esetén az 5 primosztó második hatványon jelenik meg stb.).
  • Ha megtaláltuk 'm' egy 'j' primosztóját, akkor az 'm' változó értékét osztjuk 'j'-vel (és utána a 'k' ciklusváltozót a 'for' ciklus növeli eggyel).
    • Ha 'm' értéke 1 (m==1), akkor az összes primosztót megtaláltuk, ezért kiléphetünk mindkét ciklusból (break cikl;).
  • Ha 'm'-nek 'j' már nem primosztója, akkor kilépünk a második ("belső") 'for' ciklusból (break;).

Az előző programban a kiírások megváltoztatásával könnyen kiíratható egy természetes szám primszámok szorzataként:

/* egy szám összes primosztója szorzatalakban */

function primszam(i) {
 var prim=true;
 for(var j=2;j<=Math.sqrt(i);j++) {
  var q=i/j;
  if(Math.trunc(q)*j==i) {
   prim=false;
   break;
   }
  }
 return prim;
 }

var n=2450;
var m=n;

write(n+"=");
var elso=true;

cikl: 
for(var j=2;j<=n;j++) {
 for(var k=1;k<=n;k++) {
  var q=m/j;
  if(Math.trunc(q)*j==m && primszam(j)) {
   if(elso) {
    write(j);
    elso=false;
    }
   else {
    write("*"+j);
    }
   m=q;
   if(m==1) break cikl;
   }
  else {
   break;
   }
  }
 }
writeln();

writeln();
writeln("-----");

A program képernyőképe a következő:

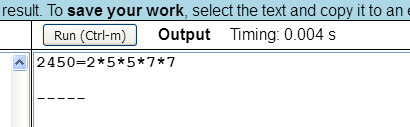
Próbáljunk meg önállóan válaszolni arra a kérdésre, hogy a programban mi a szerepe az 'elso' változónak?

Gyakorló feladatok:

A korábban megismert sorozatok első 'n' eleme közül válogassa ki a primszámokat!

JavaScript összefoglaló

a JavaScript nyelvi elemei

Írjon be egy adatot:

[elemi adattípusok, adatok (literálok)]

• számok ( number, pl. 3, -4.22, 2.19e-3, 0x1a )
  • karakterlánccá vagy stringgé alakítás (pl. legyen var x=7.12917; ekkor String(x) → "7.12917")
    • kerekítés adott számú tizedesjegyre (pl. x.toFixed(2) → "7.13", x.toFixed(3) → "7.129"; megjegyzés: a toFixed függvény egy számot stringgé alakít)
  • logikai értékké alakítás (pl. Boolean(1) → true; Boolean(0) → false)
• karakterláncok, stringek ( string; pl. var s="hello")
  • karakterek (pl. "a")
    • karakter közvetlen megadása a karakter hexadecimális kódjával (pl. "\x23" vagy "\u0023" → #, "\u2283" → ⊃ )
    • egy karakter kódjának megállapítása (pl. "a".charCodeAt(0) → 97)
    • karakter megadása a karakter kódjával (pl. String.fromCharCode(35) vagy String.fromCharCode(0x23) → # , String.fromCharCode(0x2284) → ⊄ )
    • speciális karakterek megadása (pl. \" → idézőjel megadása egy stringen belül; \n → soremelés)
  • stringek decimális számmá alakítása (pl. Number("3.14") → 3.14; Number("Hello") → NaN; 1/0 → Infinity)
    • var x=Number("Hello"); if(isNaN(x)) x="(nem szám)";
    • var x=1/0; if(!isFinite(x)) x=(túlcsordulás);
    • var x=parseFloat("12.46"); (valós számmá alakítás)
    • var x=parseInt("12.46"); (egész számmá alakítás a tizedesjegyek levágásával)
      • var x=parseInt("1010",2); (bináris szám decimális számmá alakítása)
      • var x=parseInt("a0",16); (hexadecimális szám decimális számmá alakítása)
  • decimális számok stringgé alakítása adott számrendszerben
    • decimális számrendszerben (pl. var d=Number(123).toString(); d → "123";)
    • hexadecimális számrendszerben (pl. var h=Number(123).toString(16); h → "7b";)
    • bináris számrendszerben (pl. var b=Number(123).toString(2); b → "1111011";)
  • logikai értékké alakítás (pl. Boolean("1") → true; Boolean("0") → false)
• logikai értékek ( boolean; pl. true, false )
  • számmá alakítás (pl. Number(true) → 1; Number(false) → 0)
  • karakterlánccá alakítás (pl. String(true) → "true"; String(false) → "false")

[változók, változótípusok]

[elemi típusú változók]

• var x=13; ( typeof(x) → number )
• var s="hello"; ( typeof(s) → string; s.length → 5 )
  • ( s[0] → "h"; s[4] → "o" )
  • ( s.substring(3,5) → "lo" )
• var b=true; ( typeof(b) → boolean )

// számrendszerek

var x,d,b,h;

x=123;
d=Number(x).toString();
writeln(x+" | "+d);

x=123;
b=Number(x).toString(2);
writeln(x+" | "+b);

x=123;
h=Number(x).toString(16);
writeln(x+" | "+h);

writeln("--------------------------------------------------");

b="10110100";
x=parseInt(b,2)
writeln(x+" | "+b);

h="2cd";
x=parseInt(h,16)
writeln(x+" | "+h);

writeln("--------------------------------------------------");

b="10101010";

write(b+" közvetlen átváltása decimális számrendszerbe: ");
x=1*128+0*64+1*32+0*16+1*8+0*4+1*2+0*1;
writeln(x);

x=0; // részösszegek
he=1; // helyiérték
i=b.length-1; // ciklusváltozó

while(i>=0) {
 d=parseInt(b.charAt(i),2); // számjegy adott helyiértéken
 x+=d*he; // vagy x=x+d*he;
 he*=2; // vagy he=he*2;
 i--; // vagy i=i-1;
 }

writeln(b+"  -->  "+x);
writeln("--------------------------------------------------");

h="3de5";

write(h+" közvetlen átváltása decimális számrendszerbe: ");
x=3*16**3+13*16**2+14*16+5*1;
writeln(x);

x=0; // részösszegek
he=1; // helyiérték
i=h.length-1; // ciklusváltozó

while(i>=0) {
 d=parseInt(h.charAt(i),16); // számjegy adott helyiértéken
 x+=d*he; // vagy x=x+d*he;
 he*=16; // vagy he=he*16;
 i--; // vagy i=i-1;
 }

writeln(h+"  -->  "+x);
writeln("--------------------------------------------------");

[egy- és többdimenziós tömbök (array)]

• var szamok=[1,4,3,1]; ( typeof(szamok) → object; szamok.length → 4 )
  • ( typeof(szamok[0]) → number )
  • var rend1=szamok.sort(); (lexikografikus rendezés);
  • function vizsgalat(a,b) { return a-b; }
    var rend2=szamok.sort(vizsgalat); (nagyság szerinti rendezés);
• var szamok=[4,2,8,1,["alma","szilva"]]; ( typeof(szamok) → object; szamok.length → 5 )
  • ( typeof(szamok[0]) → number )
  • ( typeof(szamok[4]) → object; szamok[4].length → 2 )
    • ( typeof(szamok[4][0]) → string )

Egy példa egydimenziós tömbök létrehozására:

// egydimenziós tömbök

var tanulok=["Jancsi","Zoe","Peti","Kata","Ildi"];
var i;

tanulok[5]="Tercsi"; // vagy tanulok[this.length]="Tercsi";
tanulok[6]="Fercsi";

writeln("Névsor:\n");

for(i=0;i<tanulok.length;i++) {
 writeln(tanulok[i]);
 }

writeln("\nÖsszesen "+tanulok.length+" tanuló.\n");

writeln("--------------------------------------------------");

tanulok.sort();

writeln("Rendezett névsor:\n");

for(i=0;i<tanulok.length;i++) {
 writeln(tanulok[i]);
 }

writeln("--------------------------------------------------");

Egy példa egydimenziós, számokból álló tömbök (vektorok) létrehozására és a tömb elemeinek összeadására:

// számok (tömbelemek) összeadása

var szamok=[1,4,3,2];
var i,osszeg=0;

for(i=0;i<szamok.length;i++) {
 osszeg+=szamok[i];
 // if(i+1>=szamok.length) break;
 writeln("részösszeg: "+osszeg);
 }

writeln("\nvégösszeg: "+osszeg);

writeln("--------------------------------------------------");

Egy példa többdimenziós tömbök (mátrixok) létrehozására és kiírására:

// többdimenziós tömbök (mátrixok) létrehozása

// négyzetes mátrix

var i,j;
var matrix=[
 [1,4,3,2],
 [6,1,5,5],
 [1,2,3,4],
 [7,1,2,6]
 ];

for(i=0;i<matrix.length;i++) {
 for(j=0;j<matrix.length;j++) {
  write(matrix[i][j]+" ");
  }
 writeln();
 }

writeln("--------------------------------------------------");

// általános mátrix

matrix=[
 [1,4,3,2,8],
 [6,1,5,5,0],
 [1,2,3,4,9],
 [7,1,2,6,4]
 ];

// 4 sor és 4 oszlop kiírása

for(i=0;i<matrix.length;i++) {
 for(j=0;j<matrix.length;j++) {
  write(matrix[i][j]+" ");
  }
 writeln();
 }

writeln();

// 4 sor és 5 oszlop kiírása

for(i=0;i<matrix.length;i++) {
 for(j=0;j<matrix[i].length;j++) {
  write(matrix[i][j]+" ");
  }
 writeln();
 }

writeln("--------------------------------------------------");

[objektumok]

• var p=null; ( typeof(p) → object )
• var nevek={nev:"Kovács János", kor:23}; ( typeof(nevek) → object )
  • ( typeof(nevek.nev) → string )
  • ( typeof(nevek.kor) → number )

[nem definiált értékű és típusú változók]

• var x; ( typeof(x) → undefined )

Az azonosítók (pl. a változók neve) esetében tartsuk be a következőket: a nevek kezdődjenek kisbetűvel és csak betűket, számjegyeket, és aláhúzás-karaktert (_) tartalmazzanak. Az azonosítók neveiben a nagy- és kisbetűk különbözőek, nagybetűt csak kivételes esetben használjunk (pl. két szóból álló név esetén, szóköz helyett: tanuloNeve, tanarNeve stb.), és a magyar ékezetes betűket a nevekben ne használjuk.

[operátorok, függvények]

aritmetikai operátorok

• x=3+4; x=x+3; x+=1; (összeadás)
• y=7.14-4.31; y=x-5; y-=3; (kivonás)
• z=3.14*r; z*=2; (szorzás)
• t=2.71/v; t/=3; (osztás)
• a=b**3; b=Math.pow(2,3.4); (hatványozás)
• b=i%2; (maradékképzés, "modulo n" kiszámítása)
• i++; (növelés eggyel, +1 hozzáadása; "inkrementálás")
• j--; (csökkentés eggyel, -1 hozzáadása; "dekrementálás")

logikai operátorok

• a=!b; (negáció, tagadás; "not")
• a=p && q; (konjunkció; "and")
• a=p || q; (diszjunkció; "or")

Lássunk néhány példát a logikai operátorok használatára:

// igazságtáblázat készítése (implikáció)

function imp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!a || b;
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"⊃");
writeln("A"+" " +"B"+" "+"\u2283");
writeln("-----");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(i+" " +j+" "+imp(i,j));
  }
 }

writeln("--------------------------------------------------");

Készítsük el a

geza(A,B) = ( A ⊃ ( A ⊃ B) ) ∨. A

és a

peti(A,B) = ( ( A ⊃ B) ⊃ A ) ∨. A

logikai függvények igazságtáblázatát:

// geza(A,B) = ( A ⊃ ( A ⊃ B) ) ∨. ⌝A
// peti(A,B) = ( ( A ⊃ B) ⊃ A ) ∨. ⌝A

function imp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!a || b;
 return Number(c);
 }

function geza(x,y) {
 var a=Boolean(x), b=Boolean(y);
// var c=(imp(x,imp(x,y))) || !a;
// var c=(imp(a,imp(a,b))) || !a;
  var c=(!a || (!a || b)) || !a;
 return Number(c);
 }

function peti(x,y) {
 var a=Boolean(x), b=Boolean(y);
// var c=(imp(imp(x,y),x)) || !a;
// var c=(imp(imp(a,b),a)) || !a;
  var c=(!(!a || b) || a) || !a;
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"(A g B)");
writeln("-----------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(i+" " +j+"    "+geza(i,j));
  }
 }

writeln("--------------------------");

writeln("A"+" " +"B"+" "+"(A p B)");
writeln("-----------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(i+" " +j+"    "+peti(i,j));
  }
 }

writeln("--------------------------");

Készítsük el a kata(A,B) = ( A ∧ ( A ⊃ B) ) logikai függvény igazságtáblázatát:

// kata(A,B) = ( A ∧ ( A ⊃ B) ) 

function imp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!a || b;
 return Number(c);
 }

function kata(x,y) {
 var a=Boolean(x), b=Boolean(y);
// var c=a && imp(x,y);
// var c=a && imp(a,b);
 var c=a && (!a || b);
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"(A k B)");
writeln("-----------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(i+" " +j+"    "+kata(i,j));
  }
 }

writeln("--------------------------");

Végül egy összetettebb példa: készítsük el az mp(A,B) = ( A ∧ ( A ⊃ B) ) ⊃. B logikai függvény igazságtáblázatát, valamint Quine-táblázatát:

// mp(A,B) = ( A ∧ ( A ⊃ B) ) ⊃. B (modus ponens)

function imp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!a || b;
 return Number(c);
 }

function mp(x,y) {
 var a=Boolean(x), b=Boolean(y);
 var c=!(a && (!a || b)) || b;
 return Number(c);
 }

writeln("A"+" " +"B"+" "+"mp(A,B)");
writeln("-----------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(i+" " +j+"     "+mp(i,j));
  }
 }

writeln("--------------------------------------------------");

writeln("( A ∧ ( A ⊃ B) ) ⊃. B");
writeln("-----------");

for(i=0;i<=1;i++) {
 for(j=0;j<=1;j++) {
  writeln(" "+
         i+" " +
         Number(i && imp(i,j))+"  "+  
         i+" "+
         imp(i,j)+" "+
         j+" | "+
         mp(i,j)+" | "+
         j);
  }
 }

writeln("--------------------------------------------------");

Megjegyzések:

(I.) Az mp(A,B) = ( A ∧ ( A ⊃ B) ) ⊃. B logikai függvény Quine-táblázatában a belső ( A ∧ ( A ⊃ B) ) konjunkciót (i && imp(i,j)) módon állíthatjuk elő (A ↔ i, B ↔ j), mert az 'i' ciklusváltozó 0 vagy 1 értékű szám, amelyet a && logikai operátor használata miatt a JavaScript interpreter automatikusan logikai (Boolean) értékké alakít át. Azonban a kifejezés értéke logikai érték (true vagy false) lesz, amit a táblázatban számként (1 vagy 0) akarunk megjeleníteni, tehát a logikai kifejezés értékét számmá kell alakítanunk Number(Boolean(i) && imp(i,j)) módon.

(II.) A modus ponens következtetési szabálynak megfelelő logikai törvény levezethető a logikai azonosságokból:

( A ∧ ( A ⊃ B) ) ⊃. B ~ ( A ∧ ( A ∨ B) ) ⊃. B (az implikáció átalakítása)
( A ∧ ( A ∨ B) ) ⊃. B ~ ( ( A ∧ A ) ∨ ( A ∧ B) ) ⊃. B (disztributivitás)
( ( A ∧ A ) ∨ ( A ∧ B) ) ⊃. B ~ ( A ∧ B ) ⊃. B (az ellentmondás törvénye és a ⊥ ∨ P ~ P kiszámítási törvény)
( A ∧ B ) ⊃. B ~ ( A ∧ B ) ∨ B (az implikáció átalakítása)
( A ∧ B ) ∨ B ~ ( A ∨ B ) ∨ B (De Morgan-azonosság)
( A ∨ B ) ∨ B ~ A ∨ ( B ∨ B ) (asszociativitás)
A ∨ ( B ∨ B ) ~ ⊤ (a kizárt harmadik törvénye és a P ∨ ⊤ ~ ⊤ kiszámítási törvény).

Vagyis az mp(A,B) = ( A ∧ ( A ⊃ B) ) ⊃. B logikai függvény tautológia.

összehasonlító operátorok

• a == b (egyenlő érték; pl. i%2==1 vagy s=="alma")
  • x === y (egyenlő érték és azonos típus)
• a != b (nem egyenlő érték)
  • x !== y (különböző érték vagy különböző típus)
• x > y (nagyobb, mint)
• x >= y (nagyobb-egyenlő, mint)
• x < y (kisebb, mint)
• x <= y (kisebb-egyenlő, mint)
• ( x<y ? x : y) (feltételes kifejezés; a '?' ún. feltételes, "ternary" operator)

matematikai állandók, függvények (Math osztály)

• Math.PI (a Math.PI egy ún. nevesített konstans, amelyet a 'π' szám helyett használhatunk; π értéke → 3.14...)
  • var r=Math.PI*d/180; (ha d egy szög értéke fokban megadva, akkor r a szög értékét fogja tartalmazni radiánban vagy ívmértékben megadva)
  • var d=180*r/Math.PI; (ha r egy szög értéke radiánban vagy ívmértékben megadva, akkor d a szög értékét fogja tartalmazni fokban megadva)
• Math.E (a Math.E egy ún. nevesített konstans, amelyet az 'e' szám helyett használhatunk; az 'e' értéke → 2.718...)
• var y=Math.abs(x); (abszolút érték)
• var y=Math.sin(x), z=Math.cos(x); (szinusz és koszinusz függvény; az 'x' értékét radiánban kell megadni)
  • var y=Math.asin(x); (arkusz szinusz függvény; az 'x' értékét radiánban kapjuk meg −π/2 és π/2 közötti értékként; pl. 2*Math.asin(1)=3.141592653589793)
  • var y=Math.acos(x); (arkusz koszinusz függvény; az 'x' értékét radiánban kapjuk meg 0 és π közötti értékként; pl. 2*Math.acos(0)=3.141592653589793)
• var y=Math.tan(x); (tangens függvény; az 'x' értékét radiánban kell megadni)
  • var y=Math.atan(x) (arkusz tangens függvény; az 'x' értékét radiánban kapjuk meg −π/2 és π/2 közötti értékként; pl. 4*Math.atan(1)=3.141592653589793)
• var y=Math.round(x); (kerekítés a legközelebbi egész számra)
  • var y=Math.ceil(x), z=Math.floor(x); (felfele és lefele kerekítés a legközelebbi egész számra)
  • var y=Math.trunc(x); (tizedesjegyek levágása; vö. parseInt)
• var y=Math.exp(x1), z=Math.log(x2); (az exponenciális függvény és a természetes vagy 'e' alapú logaritmusfüggvény értéke)
• var y=Math.pow(x,n); (az xⁿ hatványfüggvény értéke)
• var ymin=Math.min(x1,x2), ymax=Math.max(x1,x2); (a legkisebb és legnagyobb szám kiválasztása; kettőnél több argumentumra is működik!)
• var x=Math.random(); (egy véletlen szám generálása a [0, 1) intervallumból)
  • Math.floor((Math.random()*90)+1); (egy véletlen egész szám generálása az [1, 90] intervallumból)

// kör kerülete és területe

var kor_sugara, x,xk,xt;

kor_sugara=4;
xk=(2*kor_sugara*Math.PI);

writeln("kerület = "+xk);
x=Math.round(xk*100)/100;
// x=xk.toFixed(2);
writeln("kerület (közelítőleg) = "+x);

writeln("--------------------------------------------------");

xt=kor_sugara*kor_sugara*Math.PI;
writeln("terület = "+xt);
x=Math.round(xt*100)/100;
// x=xt.toFixed(2);
writeln("terület (közelítőleg) = "+x);

writeln("--------------------------------------------------");

karakterláncokkal kapcsolatos függvények, operátorok, elemváltozók, metódusok (String osztály)

• var s="Hello!", x=s.length; (karakterlánc hossza; x → 6)
• var s1="John"; s2="Smith"; s=s1+" "+s2; (két string összefűzése, "konkatenációja"; s → "John Smith")
  • var s="alma"; s+=", körte"; (hozzáfűzés egy stringhez; s → "alma, körte")
  • var s="eper"; s=s.concat(", málna"); (hozzáfűzés egy stringhez; s → "eper, málna")
• var s="Hello", ch=s.charAt(0); (a string egy karaktere; ch → 'H')
  • var s="Hello", ch=s[1]; (a string egy karaktere; ch → 'e')
  • var s="H", u=s.charCodeAt(0); (a string egy karakterének UNICODE kódja; u → 72)
  • var ch=String.fromCharCode(72); (egy karakter előállítása a karakter UNICODE kódja alapján; ch → 'H')
• var s=trim("   Hello!   "); (a string vezető és záró elválasztó (szóköz, tab stb.) karaktereinek levágása; s → "Hello!")
• var s="alma", s1=s.substring(2,4); (a string egy részstringje; s1 → "ma")
• var s="alma", s1=s.replace("a","A"); (kicseréli a string egy részstringjének az első előfordulását a második paraméterként megadott stringre; s1 → "Alma")
• var s="katica"; writeln(s.indexOf("a")); (karakterlánc keresése; → 1)
  • var s="katica"; writeln(s.indexOf("a",2)); (karakterlánc keresése adott pozíciótól kezdve; → 5)
  • var s="katica"; writeln(s.indexOf("x")); (nem létező karakterlánc keresése; → -1)
• var s="4.12", s1=s.substring(".",","); (a "." első előfordulásának kicserélése "," karakterre; s1 → "4,12")

// betűk kiírása egymás alá

var s;
var idezojel="?"; // stringen belül nem lehet közvetlenül megadni
var i;

s="Hello!";
for(i=0;i<s.length;i++){
 writeln(s.charAt(i));
 }

writeln("--------------------------------------------------");

// betűk kiírása egymás mellé, szóközzel elválasztva

s="HELLO-BELLO";
for(i=0;i<s.length;i++){
 write(s.charAt(i)+" "); 
 }

writeln();
writeln("--------------------------------------------------");

// az idézőjel kódját megnéztük a Google-val (34 vagy 0x22)
// idezojel=String.fromCharCode(34);
idezojel="\u0022";

s="alma kajszibarack";
// writeln("Az \""+s+"\" string hossza: "+s.length);
writeln("Az "+idezojel+s+idezojel+ " string hossza: "+s.length);

writeln("--------------------------------------------------");

i=0;
while(i<s.length) {
writeln("Az "+idezojel+
 s.substring(0,4)+"..."+
 idezojel+
 " string "+i+"-dik karaktere: "+
 s.charAt(i));
 i++;
 }

writeln("--------------------------------------------------");

adatok bevitele és kiírása

Egy egyszerű bekezdés

adatok bevitele

• var s="Hello"; (adat beírása közvetlenül a programba; értékadás egy változónak)
• var s=document.getElementById("bekezdes").innerHTML; (az id="bekezdes" azonosítójú HTML elem tartalmának beolvasása)
  • A bekezdés tartalmának kiolvasása:
  • var s=document.getElementById("szoveg").value; (az id="szoveg" azonosítójú szövegbeviteli mező tartalmának beolvasása)
  • a táblázat tartalmának kiírása:
• var s=window.prompt("Írja be a nevét: ","<John Smith>"); (tartalom beolvasása egy felnyíló, "popup" ablak szövegsorából)
  • var x=prompt("Írjon be egy számot: "); (egy adat beolvasása; az online JavaScript interpreterben is használható)

adatok kiírása

• document.getElementById("bekezdes").innerHTML="Hello"; (az id="bekezdes" azonosítójú HTML elem tartalmának megváltoztatása)
  • Írjon be egy szöveget a bekezdésben levő tartalom megváltoztatásához:
  • document.getElementById("bekezdesszoveg").value="Hello"; (az id="bekezdesszoveg" azonosítójú szövegbeviteli mező tartalmának megváltoztatása)
• document.write("Hello "); vagy document.writeln("Hello!"); (tartalom beírása a weblap aktuális pozíciójába)
  • write("Szia "); vagy writeln("Hello!"); (tartalom kiírása az online JavaScript interpreter jobb oldali paneljében)
• window.alert("Hello!"); (tartalom kiírása egy felnyíló, "popup" ablakban)
  • s="John"; alert("Hello "+s+"!"); (üdvözlet kiírása egy felnyíló, "popup" ablakban; az online JavaScript interpreterben is használható)
• console.log("Hello"); (tartalom kiírása a böngésző F12-vel megnyitott konzoljába)

vezérlési szerkezetek

utasításblokkok

• { s="Hello"; window.alert(s); } (az utasítások kezelése egy utasításként; a blokk kezdetét jelző { nyitó kapcsos zárójel után minden új sort érdemes egy szóközzel beljebb kezdeni addig, amíg a blokk végét jelző } záró kapcsos zárójelhez nem értünk)

függvények

• function kiir(x) { writeln(x); return; } (eljárás; pl. kiir("Hello!"); az online JavaScript interpreterben kiírja az eljárás meghívásakor megadott Hello! értéket a jobb oldali panelben)
• function imp(x,y) { var a=Boolean(x), b=Boolean(y); var c=!a || b; return Number(c); } (függvény; a függvény az x ⊃ y implikációt mint logikai műveletet valósítja meg; a függvény bemeneti értékei a {0, 1} számok, a függvény logikai értékeken hajt végre műveleteket, és a kimenete a {0, 1} számok valamelyike lesz)

ciklusok

Hozzuk létre a 'szamok' tömböt pl. var szamok=[1,4,3,2]; módon!

• for(i=0; i<szamok.length; i++) { writeln(szamok[i]); } (rögzített lépésszámú ciklus)
  • for(i in szamok) { writeln(szamok[i]); } (egy tömb elemein végigfutó ciklus; bármely objektumra használható)
  • cikl: for(i=0; i<szamok.length; i++) { writeln(szamok[i]); } (rögzített lépésszámú ciklus címke megadásával)
    • continue; continue cikl; (a ciklusmag további részének figyelmen kívül hagyása)
    • break; vagy break cikl; (kilépés a ciklusból)
• i=0; while(i<szamok.length) { writeln(szamok[i]); i++; } (előltesztelő ciklus)
  • ( continue, break ld. korábban )
• i=0; do { writeln(szamok[i]); i++; } while(i<szamok.length) (hátultesztelő ciklus)
  • ( continue, break ld. korábban )

// egyszerű ciklusok

var i,m,n,s;

writeln("első 5 természetes szám (while):\n"); 

i=1;
while(i<=5) {
 writeln(i);
 i++;
 }

writeln("--------------------------------------------------");

writeln("első 5 természetes szám (for):\n"); 
for(i=1;i<=5;i++) {
 writeln(i);
 }

writeln("--------------------------------------------------");

m=3;
n=10;
writeln("'m' és 'n' közötti természetes számok:\n"); 
for(i=m;i<=n;i++) {
 writeln(i);
 }

writeln("--------------------------------------------------");

s="A";
writeln("sok 'A' kiírása:\n"); 
i=0;
while(i<5){
 writeln((i+1)+"-dik ismétlés: "+s);
 s+="A";
 i++; 
 }

writeln("--------------------------------------------------");

elágazások

• if(i>10) { i=0; } (egyirányú elágazás)
• if(x<y) { z=x; } else { z=y; } (kétirányú elágazás)
• s=""; switch(i) { case 5: s="jeles"; break; case 4: s="jó"; break; default: s="egyéb"; } (kétirányú elágazás)

// páros számok kiíratása

var i,n=10;

for(i=1;i<=n;i++) {
 if(i%2==0) {
  writeln(i);
  }
 }

writeln("--------------------------------------------------");

// hárommal osztható számok kiíratása

for(i=1;i<=n;i++) {
 if(i%3==0) {
  writeln(i);
  }
 }

writeln("--------------------------------------------------");

// hárommal osztható páros számok kiíratása

for(i=1;i<=n;i++) {
 if(i%2==0 && i%3==0) {
  writeln(i);
  }
 }

writeln("--------------------------------------------------");

Irodalomjegyzék

Moncur, Michael 2006. Tanuljuk meg a JavaScript használatát 24 óra alatt. [SAMS Teach Yourself HTML and CSS in 24 Hours.] Budapest: Kiskapu.

Suehring, Steven; Valade, Janet 2014. PHP, MySQL, JavaScript és HTML5. Budapest: Panem K. (Tantusz könyvek)

Internetes források

Online JavaScript Interpreter by Peter Jipsen, Chapman University (January 2013).
http://math.chapman.edu/~jipsen/js/ (2018-12-12)

W3Schools Online Web Tutorials.
https://www.w3schools.com/ (2018-11-23)

JavaScript Tutorial.
https://www.w3schools.com/js/ (2018-12-12)

JavaScript and HTML DOM Reference.
https://www.w3schools.com/jsref/default.asp (2018-12-12)

JavaScript Global Reference.
https://www.w3schools.com/jsref/jsref_obj_global.asp (2018-12-12)

JavaScript - Wikipédia.
https://hu.wikipedia.org/wiki/JavaScript (2020-03-22)

A JavaScript programozási nyelv. (Programnyelvek portál.)
http://nyelvek.inf.elte.hu/leirasok/JavaScript/index.php?chapter=24 (2018-12-12)

Számsorozat fogalma | | Matekarcok.
https://matekarcok.hu/szamsorozat-fogalma/ (2020-03-27)