3.2. Rendezési relációk
Legyen 'A' tetszőleges halmaz. Az 'A' halmazon értelmezett
ρ⊆AΧA
kétváltozós (binér) relációt reflexív (vagy "gyenge") rendezési relációnak nevezzük, ha reflexív, antiszimmetrikus és tranzitív.
Legyen 'A' tetszőleges halmaz. Az 'A' halmazon értelmezett
ρ⊆AΧA
kétváltozós (binér) relációt irreflexív (vagy "szigorú") rendezési relációnak nevezzük, ha irreflexív, aszimmetrikus és tranzitív.
Ha az 'A' halmazon értelmezve van egy ρ rendezési reláció, azt (A; ρ) módon jelöljük.
- Ha a ρ rendezési reláció trichotóm, akkor teljes rendezési relációnak nevezzük, az (A; ρ) halmazt pedig teljesen rendezett halmaznak (a ρ reláció szerint)
(szokásos a lineárisan rendezett halmaz elnevezés is, Szendrei 1975: 41);
- ha a ρ rendezési reláció nem trichotóm, akkor parciális rendezési relációnak nevezzük, az (A; ρ) halmazt pedig részben (vagy parciálisan) rendezett halmaznak (a ρ reláció szerint).
Például a természetes számokon (ℕ) értelmezett
- "kisebb-egyenlő, mint" ( ≤ ) és "nagyobb-egyenlő, mint" ( ≥ ) relációk gyenge és teljes rendezési relációk, mert reflexívek, antiszimmetrikusak és tranzitívek, valamint trichotómak;
- "kisebb, mint" ( < ) és "nagyobb, mint" ( > ) relációk szigorú és teljes rendezési relációk, mert irreflexívek, aszimmetrikusak és tranzitívek, valamint trichotómak.
- oszthatóság ( | ) gyenge és parciális rendezési reláció, mert reflexív, antiszimmetrikus és tranzitív, azonban nem trichotóm (mivel pl. a 3 és 7 természetes számok nem osztói egymásnak, és nem egyenlőek);
Például az 'I' halmaz 2I hatványhalmazán (azaz az 'I' halmaz összes részhalmazának halmazán) értelmezett
- részhalmaz (⊆) reláció gyenge és parciális rendezési reláció a 2I hatványhalmazon, mert reflexív, antiszimmetrikus és tranzitív, de nem trichotóm; tehát (2I; ⊆) parciálisan rendezett halmaz
(mivel pl. az {a,b} és {a,c} halmazok között sem a részhalmaz reláció, sem az egyenlőség nem áll fenn, a ⊆ reláció nem trichotóm);
- valódi részhalmaz (⊂ ) reláció szigorú és parciális rendezési reláció a 2I hatványhalmazon, mert irreflexív, aszimmetrikus és tranzitív, de nem trichotóm; tehát (2I; ⊂) szintén parciálisan rendezett halmaz
Legyen az (A; ρ) halmaz részben rendezett. Vezessük be az egymással rendezési relációban levő a, b∈A elemekre az
a≼b ⇋ ρ(a,b)
jelölést (a≼b ⇋ "a előtte van b-nek" vagy "a megelőzi b-t").
Láttuk korábban, hogy minden binér reláció ábrázolható egy irányított gráf segítségével. Rendezési relációk esetén a gráf ábrázolása jelentősen leegyszerűsíthető.
Ha az (A; ρ) részben rendezett halmaz véges, akkor ábrázolhatjuk egy irányított gráf, az ún. Hasse-diagram segítségével.
A Hasse-diagramot a következőképpen állíthatjuk elő:
- az 'A' halmaz elemeit a gráf csomópontjaiként ábrázoljuk;
- csak azok között az x, y∈A (x≠y) elemek között rajzolunk élt, amelyekre
- egyrészt x≼y teljesül,
- másrészt nem létezik olyan "köztes" z∈A (z≠x, z≠y) elem, amelyre x≼z≼y teljesül (ilyenkor azt mondjuk, hogy az 'x' elem közvetlenül megelőzi az 'y' elemet, vagy másképpen az 'y' elem fedi az 'x' elemet, vö. Kiss 2007: 336)
;
- a gyenge rendezési reláció reflexivitásából⇒ adódó hurokéleket a diagramon nem ábrázoljuk;⇒
- ha az x, y∈A (x≠y) elemekre x≼y teljesül, akkor x-et lejjebb, y-t feljebb ábrázoljuk. Ilyen ábrázolás esetén a csomópontok elhelyezkedése meghatározza a relációt jelző él irányát (mivel az élek mindig felfelé mutatnak, a gráfban a rendezési reláció irányát követve "felfelé haladunk"), ezért a relációban álló csomópontokat irányítás nélkül is összeköthetjük.
A Hasse-diagram két fontos tulajdonsága:
- a diagramban, ha kiindulunk egy csomópontból, az élek irányában haladva sosem jutunk vissza a kiinduló csomópontba (a rendezési reláció antiszimmetriája és tranzitivitása miatt a diagram nem tartalmaz önmagába záruló irányított utat, "kört")
- ha a diagramot "fejjel lefelé" fordítjuk, egy "duális" Hasse-diagramhoz jutunk, ahol
- az első diagram az (A; ≼) rendezésnek felel meg
- a második diagram pedig az (A; ≽) rendezésnek felel meg (ahol a≽b ⇔ b≼a teljesül)
Például ábrázoljuk az A={a, b, c} halmaz esetén a (2A; ⊆) részben rendezett halmaz elemeit Hasse-diagrammal:
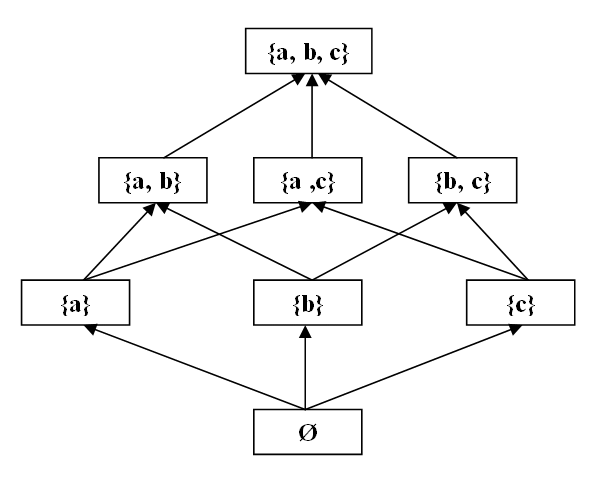
Szemléletesen azt is mondhatjuk, hogy a fenti diagramon az üreshalmaz a "legkisebb" (legalsó) elem, amely minden elemnek részhalmaza; az A={a, b, c} halmaz pedig a "legnagyobb" (legfelső) elem, amelynek minden, az ábrán szereplő elem a részhalmaza.
Figyeljük meg, hogy egyes csomópontokból több él indulhat ki, bizonyos csomópontokba több él futhat be, és a "legkisebb" elemből több különböző irányított úton keresztül is eljuthatunk a "legnagyobb" elemhez. Visszafelé azonban egyetlen csomópontból sem vezet út, a fenti diagramon csak "felfelé" haladhatunk.
Korábban már ábrázoltuk táblázatos formában egy három elemű alaphalmaz részhalmazai között értelmezett részhalmaz relációt.⇒ Ábrázoljuk most az
A={a b c}
alaphalmaz tetszőleges
P, Q∈2A
elemei közötti részhalmaz relációt (P⊆Q) egy táblázatban a következőképpen:
– a relációban álló elemeket a megfelelő cellában 1 értékkel jelöljük;
– a "közvetlenül" relációban álló (egymást fedő) elemeket a megfelelő cellában piros színnel kiemeljük, a "nem közvetlenül" relációban álló elemek esetében pedig fekete háttért alkalmazunk;
– a relációban nem álló elemeket pedig a megfelelő cellában 0 értékkel jelöljük.
|
P⊆Q
| ←Q→
|
|
↓P↓
| ∅
| {a}
| {b}
| {c}
| {a,b}
| {a,c}
| {b,c}
| {a,b,c}
|
| ∅
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 1
|
| {a}
| 0
| 1
| 0
| 0
| 1
| 1
| 0
| 1
|
| {b}
| 0
| 0
| 1
| 0
| 1
| 0
| 1
| 1
|
| {c}
| 0
| 0
| 0
| 1
| 0
| 1
| 1
| 1
|
| {a,b}
| 0
| 0
| 0
| 0
| 1
| 0
| 0
| 1
|
| {a,c}
| 0
| 0
| 0
| 0
| 0
| 1
| 0
| 1
|
| {b,c}
| 0
| 0
| 0
| 0
| 0
| 0
| 1
| 1
|
| {a,b,c}
| 0
| 0
| 0
| 0
| 0
| 0
| 0
| 1
|
|
↑P↑
| ∅
| {a}
| {b}
| {c}
| {a,b}
| {a,c}
| {b,c}
| {a,b,c}
|
Figyeljük meg, hogy a Hasse-diagramon pontosan annyi élt ábrázoltunk, ahány cellában pirossal kiemelt 1 érték szerepel a táblázatban (összesen 12).
Az A={a, b, c} halmaz esetén a (2A; ⊆) részben rendezett halmaz elemeit ábrázoló Hasse-diagram számos információt szolgáltat:
- az élekkel összekötött csomópontok részhalmaz relációban (⊆) állnak (egy vagy több köztes csomópont esetén az összekötött csomópontok közötti részhalmaz relációt az ábra a reláció tranzitivitása miatt közvetve ábrázolja)
- általánosan megfogalmazva a rendezési reláció (≼) iránya alulról felfelé mutat (azaz a "kisebb" elemből a "nagyobb" elem felé) (pl. {a}→{a,b} tehát {a}⊆{a,b})
- az ábrán a "legnagyobb" elem maga az 'A' halmaz, amelynek minden, az ábrán szereplő elem a részhalmaza
- az ábrán a "legkisebb" elem az üreshalmaz (∅), amely minden elemnek részhalmaza
-
két részhalmaz unióját úgy kapjuk meg, hogy az ábrán felfelé haladva megkeressük az első (relatíve "legkisebb") olyan közös csomópontot, amelyhez mindkét részhalmazból él vezet;
például
- {a}→{a,b} és {b}→{a,b} tehát {a}∪{b}={a,b}
- {a}→{a,b}→{a,b,c} és {b,c}→{a,b,c} tehát {a}∪{b,c}={a,b,c}
- {a}→{a,b} tehát {a}∪{a,b}={a,b} (ebben a példában a közös csomópont egybeesik az egyik részhalmazzal)
-
két részhalmaz metszetét úgy kapjuk meg, hogy az ábrán lefelé haladva megkeressük az első (relatíve "legnagyobb") olyan közös csomópontot, amelyből mindkét részhalmazhoz él vezet;
például
- {a}→{a,b} és {a}→{a,c} tehát {a,b}∩{a,c}={a}
- ∅→{a} és ∅→{b}→{b,c} tehát {a}∩{b,c}=∅
- {a}→{a,b} tehát {a}∩{a,b}={a} (ebben a példában a közös csomópont most is egybeesik az egyik részhalmazzal)
Összefoglalva, ha egy 'A' halmaz összes részhalmazát a részhalmaz-reláció szerint parciálisan elrendezzük és a rendezést egy Hasse-diagramon ábrázoljuk, akkor
- Ha 'P' és 'Q' az ábrán szereplő két tetszőleges csomópont, akkor az uniójukat jelentő csomópont (C) az a "legkisebb" olyan halmaz, amelyre mind P⊆C, mind Q⊆C teljesül.⇒
- Ha 'P' és 'Q' az ábrán szereplő két tetszőleges csomópont, akkor a metszetüket jelentő csomópont (C) az a "legnagyobb" olyan halmaz, amelyre mind C⊆P, mind C⊆Q teljesül.⇒
Jegyezzük meg, hogy a fenti megállapítások akkor is teljesülnek, ha az 'A' halmaz részhalmazainak egy olyan B⊆2A halmazát rendezzük el a fenti módon, amely zárt az unióképzés és metszetképzés műveleteire (azaz bármely két P, Q∈B halmazra P∪Q∈B és P∩Q∈B teljesül).
Például ha a P⊆A és Q⊆A elemek unióját keressük, akkor
(1) induljunk ki a C0=A={a,b,c} halmazból és vizsgáljuk meg az összes C0-t közvetlenül megelőző csomópontot;
(2) ha találunk egy olyan C1→C0 elemet, amelyre mind P⊆C1 , mind Q⊆C1 teljesül (amely egybeeshet P-vel vagy Q-val), akkor a következő lépésben a C1-t közvetlenül megelőző csomópontokat vizsgáljuk meg (majd ismételjük meg ugyanezt C2→C1-re, C3→C2-re stb.);
(3) a legutolsó Ci csomópont, amelyre mind Q⊆Ci , mind P⊆Ci teljesül, éppen a keresett unió lesz, azaz Ci=Q∪P teljesül.⇒
Ezek után ábrázoljuk az A={1, 2, 3, 4} számhalmaz esetén az (A; ≤) teljesen vagy lineárisan rendezett halmaz elemeit Hasse-diagrammal. Az előző ábrával összehasonlítva figyeljük meg a parciális és teljes rendezés közötti különbséget a Hasse-diagramon:
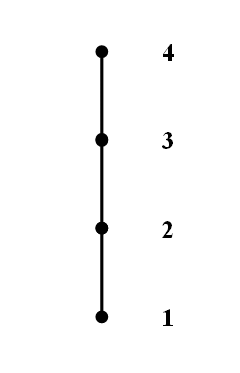
Vegyük észre, hogy a diagram a teljes rendezés miatt egy egyenesre egyszerűsödött.
Ha egy véges 'A' halmazon értelmezünk egy
ρ⊆AΧA
teljes rendezési relációt, akkor egy megfelelő algoritmus segítségével az 'A' halmaz elemei "lineárisan" sorba rendezhetők.
A parciális és teljes rendezés közötti különbséget azzal is jól tudjuk szemléltetni, ha a részben (parciálisan), ill. teljesen rendezett halmazok megfelelő elemeire értelmezzük a "legkisebb" ("legnagyobb") elem, ill. "minimális" ("maximális") elem fogalmakat.
Legyen
ρ⊆AΧA
az 'A' halmazon értelmezett (parciális vagy teljes) rendezési reláció, és vezessük be most is az egymással relációban levő a, b∈A elemekre az
a≼b ⇋ ρ(a,b)
jelölést.
Ekkor az (A; ≼) (részben vagy teljesen) rendezett halmaz
- legkisebb eleme az az
xlk∈A
elem, amelyre igaz, hogy minden y∈A elemre
xlk≼y
teljesül;
- legnagyobb eleme az az
xln∈A
elem, amelyre igaz, hogy minden
y∈A elemre y≼xln
teljesül;
- minimális eleme az az xmin∈A elem, amelyre igaz, hogy nem létezik olyan y∈A, y≠xmin elem, amelyre y≼xmin teljesül (vagyis nincs az 'A' halmaznak másik olyan eleme, amely a minimális elemnél "kisebb");
- maximális eleme az az xmax∈A elem, amelyre igaz, hogy nem létezik olyan y∈A, y≠xmax elem, amelyre xmax≼y teljesül (vagyis nincs az 'A' halmaznak másik olyan eleme, amely a maximális elemnél "nagyobb").
A legkisebb / legnagyobb és minimális / maximális elemekre teljesülnek az alábbi tételek:
(részben rendezett halmazokra)
Ha létezik egy részben rendezett halmaznak legnagyobb eleme, akkor az egyúttal maximális elem is.
Ha létezik egy részben rendezett halmaznak legkisebb eleme, akkor az egyúttal minimális elem is (vö. Bogya 2018: 19).
Egy részben rendezett halmazban legnagyobb, ill. legkisebb elemből legfeljebb egy darab létezhet, ugyanakkor maximális, ill. minimális elemből több is lehet (vö. Bogya 2018: 19).
(teljesen rendezett halmazokra)
Teljesen rendezett halmazok esetében a legkisebb elem és a minimális elem, valamint a legnagyobb elem és a maximális elem egybeesik (vö. Nagy 2017: 5. ea.).
Egy teljesen rendezett halmaznak legfeljebb egy minimális eleme és legfeljebb egy maximális eleme lehet (Dringó-Kátai 1986: 29).
Legyen például A={1,2,...,8}, és tekintsük az 'A' halmazon az oszthatósági relációt (amely gyenge parciális rendezési reláció). Ekkor
- az 'A' halmaz legkisebb eleme 1 (mivel 1 minden természetes számnak osztója, tehát 'A' minden elemének is osztója);
- az 'A' halmaznak legnagyobb eleme nem létezik (ugyanis 'A'-ban nincs olyan elem, amelynek 'A' minden eleme osztója lenne);
- az 'A' halmaz minimális eleme 1 (mert nincs olyan természetes szám, amely rajta kívül osztója lenne, tehát 'A' elemei között sincs ilyen szám);
- az 'A' halmaz maximális elemei az 5, 6, 7 és 8 számok (ugyanis 'A'-ban nincs olyan elem, amelynek ezek a számok osztói lennének).
Az (A; |) oszthatóság szerint részben rendezett halmaz Hasse-diagramja:

Ha az 'A' halmazt kibővítjük úgy, hogy 'A' tetszőleges két elemének legkisebb közös többszöröse is eleme legyen a halmaznak (azaz az 'A' halmaz elemein kívül a
{2,3,5,7}, {22=4,3,5,7} és {23=8,3,5,7}
számokból képezhető összes 2,3 és 4 tényezőből álló különböző részszorzat), akkor az így kapott
AK=A∪{10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70, 84, 120, 125, 140, 147, 210, 280, 420, 840}
kibővített halmaznak egy legkisebb eleme (1) lesz, amely egyben minimális elem is, és egy legnagyobb eleme lesz (23*3*5*7=840), amely egyben maximális elem is. Emellett az így képzett AK halmaz zárt lesz a halmaz elemei között értelmezett legkisebb közös többszörös (lkkt) műveletre.
Jegyezzük meg, hogy bizonyos feltételek fennállása mellett a természetes számok között értelmezett oszthatósági relációt (|) ábrázoló Hasse-diagram a korábbi, az A={a, b, c} halmaz részhalmazait ábrázoló Hasse-diagramhoz hasonló információkat szolgáltat.
(1) A részhalmazok közötti unió műveletének a diagramon ábrázolt természetes számok között értelmezett legkisebb közös többszörös (lkkt) művelet felel meg (például [2,3]=6 stb.).
(2) A részhalmazok közötti metszet műveletének pedig a diagramon ábrázolt természetes számok között értelmezett legnagyobb közös osztó (lnko) művelet felel meg (például (4,6)=2 stb.).
Mindennek az a feltétele, hogy az (A; |) részben rendezett halmaz mind az lkkt, mind az lnko műveletekre zárt legyen (a fenti diagramon ábrázolt 'A' halmazra ez nyilván nem teljesül, pl. [3,4]=12 vagy [3,5]=15 nem eleme A-nak).
Legyen
A={1, 2, 3, 5, 6, 10, 15, 30}
és ábrázoljuk az (A; |) részben rendezett halmazt Hasse-diagram segítségével:
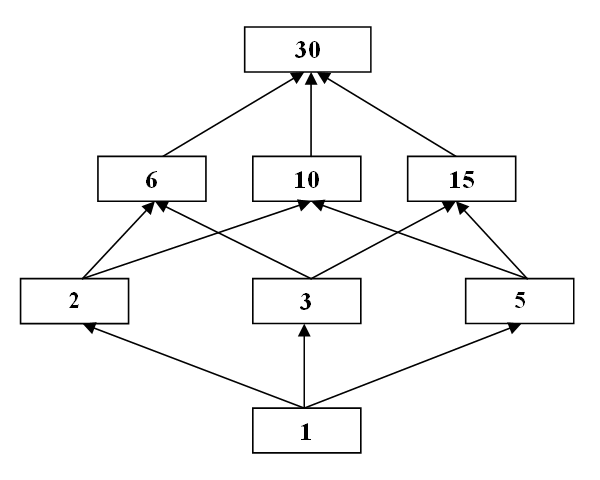
Figyeljük meg, hogy az (A; |) halmaz zárt az lkkt és az lnko műveletekre, azaz bármely két a, b∈A⊆ℕ természetes szám esetén (a,b)∈A és [a,b]∈A teljesül.

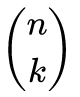 lehetséges osztályozás lehetséges ('n' elemből 'k' osztályt választunk ki az elemek sorrendjétől függetlenül), az összefüggés a binomiális tétel alapján könnyen belátható.
lehetséges osztályozás lehetséges ('n' elemből 'k' osztályt választunk ki az elemek sorrendjétől függetlenül), az összefüggés a binomiális tétel alapján könnyen belátható.