7.4. Következtetési sémák

Legyenek A, B és C tetszőleges formulák.

Az érvényes következtetések levonását számos következtetési (vagy levezetési) szabály, ún. következtetési séma segíti. Ezek olyan logikai kifejezések, amelyek egyrészt megfelelnek a következtetés általános formulájának, másrészt a bennük szereplő kijelentésváltozók minden lehetséges értékére igazak (azaz logikai törvények vagy tautológiák). Ezt a szokásos módon a ⊨ szimbólummal jelöljük.

Lássunk néhányat a fontosabb következtetési sémák vagy szabályok közül (vö. Dragálin-Buzási 1986: 110, 122-125 et passim). A szabályokat mind logikai törvényként, mind következtetési szabályként megadjuk.

(I.) Először ismerjük meg az általános következtetési sémákat. Ezek a logikai műveletek alapvető tulajdonságaiból, ill. az ezeket kifejező logikai azonosságokból⇒ közvetlenül következnek.

A két premisszával rendelkező következtetési sémákban (ún. szillogizmusokban) a premisszák közötti konjunktív (logikai "és") kapcsolatot vesszővel fogjuk jelölni, vagyis az A , B ⇋ A∧B jelölést fogjuk használni a ⊨ következtetési szimbólum előtt. (Jegyezzük meg, hogy ezt a jelőlést használtuk a logikai következményre⇒ és a követleztetésekre vonatkozó általános formula esetében is.)

Egy ⊨ A ⊃ B vagy A ⊨ B formában megadott érvényes következtetési séma azokban az esetekben használható fel értelmesen egy logikai érvelésben (egy levezetés során, bizonyításkor stb.), ha a séma előtagja (az "ok") igaz, azaz |A|=1 teljesül. Ekkor ugyanis a következtetési séma garantálja, hogy a séma utótagja (az "okozat") is igaz lesz, vagyis |B|=1 teljesül.
Azokban az esetekben, amikor a következtetési sémák előtagja hamis, azaz |A|=0 teljesül, akkor az implikáció tulajdonságai miatt az utótag lehet igaz is és hamis is, vagyis mind |B|=0, mind |B|=1 teljesülhet. Tehát hamis előtag esetén az utótag igazságértékéről nem tudunk semmit sem megállapítani.

(II.) Ezután ismerjük meg a logikai levezetésekben, ill. bizonyításokban leggyakrabban használt következtetési sémákat.

(III.) Ismerjünk meg néhány további, két premisszát tartalmazó alapvető következtetési sémát vagy szillogizmust is (Kopasz 1996: 19-20).

A modus ponens és modus tollens kognitív pszichológiai vizsgálatára alkalmazták a következő feladatot (Mérő 1994: 21-23):

E K 4 7

A fenti táblázatban négy kártya látszik. A kártyák egyik oldalán betűk, a másik oldalán számok állnak.

Tekintsük a következő állítást: ha egy kártya egyik oldalán magánhangzó van, akkor a másik oldalán páros páros szám áll.

Formálisan: vezessük be a kártyák K alaphalmazán a
    V(x) ⇋ "az x∈K kártyán magánhangzó (vowel) van"
és az
    E(x) ⇋ "az x∈K kártyán páros (even) szám van"
formulákat. A fenti állítás a ⊨ ( V ⊃ E ) logikai törvényt fogalmazza meg.

Kérdés: melyek azok a kártyák, amelyeket feltétlenül meg kell fordítanunk ahhoz, hogy eldöntsük, a fenti állítás igaz-e?

Érdekesség, hogy a vizsgálatok során a megkérdezettek 100%-a sikeresen alkalmazta a modus ponens szabályt (E választása), de a modus tollens alkalmazása már csak 57%-ban volt sikeres (7 választása).

(1) Tegyük fel, hogy az első kártyán az "E" betű mögött az "n" természetes szám szerepel. Ezt E_n módon jelölve nyilván E_n∈K. Mivel V(E_n) ("E" magánhangzó), ezért ha ⊨ V(x) ⊃ E(x) igaz minden x∈K kártyára, akkor a modus ponens szabály alapján V(E_n), V(E_n) ⊃ E(E_n)⊨E(E_n) teljesül. E(E_n) viszont azt jelenti, hogy az "E" kártya másik oldalán szereplő "n" természetes számnak páros számnak kell lennie.

(2) Tegyük fel, hogy a negyedik kártyán a "7" természetes szám mögött a "β" betű szerepel. Ezt 7_β módon jelölve nyilván 7_β∈K. Mivel ⌝E(7_β) ("7" páratlan szám), ezért ha ⊨ V(x) ⊃ E(x) igaz minden x∈K kártyára, akkor a modus tollens szabály alapján V(7_β) ⊃ E(7_β),⌝E 7_β⊨⌝V(7_β) teljesül. ⌝V(7_β) viszont azt jelenti, hogy a "7" kártya másik oldalán szereplő "β" betűnek mássalhangzónak kell lennie.

A fenti következtetési szabályokat és sémákat átalakíthatjuk úgy, hogy eredményül további, érvényes szabályokat vagy sémákat kapunk (vö. Ruzsa 1968b: 544):

Végül emeljük ki azt a korábban már említett összefüggést, amely szerint a logikai azonosságok⇒ maguk is kétirányú ("megfordítható") következtetési szabályoknak vagy sémáknak tekinthetők (vö. Borsodi 1972: 313).

Az esetelemzés szabálya⇒ például az alábbi logikai azonosság egyik következménye:
(A⊃C)∧(B⊃C) = (A∨B)⊃C

A fenti azonosság azonos átalakításokkal könnyen belátható:
    (A⊃C)∧(B⊃C) = 
    (⌝A∨C)∧(⌝B∨C) = 
    (⌝A∧⌝B)∨C = 
    ⌝(A∨B)∨C = 
    (A∨B)⊃C (q.e.d.)

A fenti logikai azonosságból az alábbi két következtetési szabályt kapjuk:

7.5. Példák következtetési sémák használatára

A következőkben példákat mutatunk be a következtetési sémák helyes használatára. Minden példát megadunk

A szöveges példák során olyan értelmes mondatokat adunk meg az iskola univerzumban (a benne levő osztályokkal, tanulókkal, tantermekkel, taneszközökkel stb.), amelyek egy adott következtetési séma helyes használatát mutatják be. A példák során a premisszák külön sorokban szerepelnek, és a belőlük levonható következtetést az alattuk levő vonal alatt adjuk meg.

Minta:

(... példa) (modus ponens)
Róza figyelmesen elolvassa és megérti a kiválasztott feladat szöveges példáját.
Ha Róza figyelmesen elolvas és megért egy feladatot, akkor meg is tudja oldani.
Róza meg tudja oldani a kiválasztott feladatot.

(1) A szöveges példákban szereplő állítások rendszerint nyitott mondatok, amelyek egy vagy több predikátumot és különböző típusú individuumváltozókat tartalmaznak. Az individuumváltozók meghatározott alaphalmazokból vehetnek fel értékeket (amelyeket az iskola univerzumban jól ismertnek tételezünk fel).

A fenti szöveges példában szereplő állítások esetén egy individuumváltozót használunk, amely a különböző feladatok alaphalmazából vehet fel értékeket. (Ha Róza helyett 'egy tanuló" szerepelne a mondatokban, akkor egy olyan individuumváltozót is bevezetnénk, amely a tanulók alaphalmazából vehet fel értékeket.)

(2) A példákat halmazok közötti összefüggések segítségével is megadjuk. Ezekben legyen I egy alaphalmaz, legyenek A, B, C⊆I meghatározott halmazok, x∈I pedig egy adott halmazelem (amelyekre a feladatokban megfogalmazott állítások teljesülnek).

(3) A példákban P1 és P2 jelentsenek premisszákat, és Q ezek egy lehetséges következményét.

Minden példa esetében a P1, P2 ⊨ Q következtetés teljesül.
(a1) (modus ponens)
P1 ⇋ x∈A
P2 ⇋ A⊆B
Q = x∈B

A feladatban felhasznált következtetési séma: modus ponens.⇒

Egy lehetséges megoldás:
Julcsi az 1.a osztályba jár. (P1)
Az 1.a osztály a Kossuth Általános Iskola egyik osztálya. (P2)
Julcsi a Kossuth Általános Iskolába jár. (Q)

Megjegyzés: egy iskolát olyan, tanulókból (x) álló halmaznak tekintjük, akik az adott iskolába (B), és azon belül egy meghatározott osztályba (A) járnak (vagyis x∈A, A⊆B). Az iskola ezeknek az osztályoknak az uniója (B=A1∪A2∪...∪An). Az osztályok az egyes iskoláknak, az iskolák a tanulók halmazának egy osztályozását jelentik. Ennek megfelelően feltesszük, hogy egy osztály tanulói mindannyian egy iskolába járnak, és minden tanuló egy osztályba tartozik.
A fenti példában tehát
    Julcsi (x) az 1.a osztályba (A) jár. ⇋ (x∈A);
    Az 1.a osztály (A) a Kossuth Általános Iskola (B) egyik osztálya. ⇋ A⊆B, azaz a részhalmaz reláció korábban tanult definíciója alapján minden 't' tanulóra (t∈A)⊃(t∈B) teljesül, vagyis speciálisan Julcsira (x) is igaz, hogy (x∈A)⊃(x∈B);
    Julcsi (x) a Kossuth Általános Iskolába (B) jár. ⇋ (x∈B).

A következtetés az alábbi módon igazolható. A részhalmaz reláció (⊆) definíciója miatt:⇒
P2 ⇋ "az 'A' halmaz minden eleme eleme a 'B' halmaznak is".
Ez formálisan a következőképpen írható le:
P2 ⇋ (tetszőleges x∈A esetén) x∈A ⊃ x∈B
Vegyük észre, hogy A⊆B fennállása esetén az (x∈A ⊃ x∈B) implikáció bármely x∈I elem esetén igaz, amiből a modus ponens⇒ következtetési séma alapján
x∈A , (x∈A ⊃ x∈B) ⊨ x∈B
következik. Ennek alapján
P1 , P2 ⊨ x∈B
teljesül, vagyis a keresett Q formulára
Q = x∈B
adódik.

(a2) (modus ponens)
P1 ⇋ x∈A
P2 ⇋ A⊆B;
Q = x∉B

A feladatban felhasznált következtetési séma: modus ponens (második variációja).⇒

Egy lehetséges megoldás:
Julcsi az 1.a osztályba jár. (P1)
Az 1.a osztály nem a Kossuth Általános Iskola egyik osztálya. (P2)
Julcsi nem a Kossuth Általános Iskolába jár. (Q)
(b1) (indirekt bizonyítás)
P1 ⇋ x∈A (az 'x' elem az A halmazba tartozik)
P2 ⇋ B⊆A (a 'B' halmazba nem tartozó elemek egyike sem tartozik az 'A' halmazba)
Q = x∈B

A feladatban felhasznált következtetési séma: indirekt bizonyítás.⇒

Egy lehetséges megoldás:
Julcsi az 1.a osztályba jár. (P1)
A Kossuth Általános Iskolán kívül egyetlen iskolának sincs 1.a osztálya. (P2)
Julcsi a Kossuth Általános Iskolába jár. (Q)
(b2) (indirekt bizonyítás)
P1 ⇋ x∈A
P2 ⇋ B⊆A;
Q = x∉B

A feladatban felhasznált következtetési séma: indirekt bizonyítás (második változat).⇒

Egy lehetséges megoldás:
Julcsi az 1.a osztályba jár. (P1)
A Kossuth Általános Iskolának nincs 1.a osztálya. (P2)
Julcsi nem a Kossuth Általános Iskolába jár. (Q)
(c) (modus tollens)
P1 ⇋ A⊆B
P2 ⇋ x∉B
Q = x∉A

A feladatban felhasznált következtetési séma: modus tollens.⇒

Egy lehetséges megoldás:
Az 1.a osztály a Kossuth Általános Iskola egyik osztálya. (P1)
Julcsi nem a Kossuth Általános Iskolába jár. (P2)
Julcsi nem a Kossuth Általános Iskola 1.a osztályába jár. (Q)
(d) (modus tollendo ponens)
P1 ⇋ x∈A∪B
P2 ⇋ x∉A
Q = x∈B

A feladatban felhasznált következtetési séma: modus tollendo ponens.⇒

Egy lehetséges megoldás:
Julcsi az 1.a osztályba vagy az 1.b osztályba jár. (P1)
Julcsi nem az 1.b osztályba jár. (P2)
Julcsi az 1.a osztályba jár. (Q)
(e) (de Morgan szabály és modus tollendo ponens)
P1 ⇋ x∉(A∩B)
P2 ⇋ x∈A
Q = x∉B

A feladatban felhasznált következtetési sémák: de Morgan azonosság⇒ és modus tollendo ponens⇒

Egy lehetséges megoldás:
Julcsi nem a Kossuth Általános Iskola 1.a osztályába jár. (P1)
Julcsi az 1.a osztályba jár. (P2)
Julcsi nem a Kossuth Általános Iskolába jár. (Q)

Emlékezzünk vissza rá, hogy a halmazokra vonatkozó de Morgan azonosság alapján
    (A∩B) = (A∪B)
teljesül. Ha x∈I egy tetszőleges tanuló, akkor a p ⇋ x∈A és q ⇋ x∈B kijelentésekkel ez
    ⌝(p∧q) = (⌝p∨⌝q)
módon írható le, ami éppen a kijelentésekre érvényes de Morgan azonosság. Ennek megfelelően az előző megoldás P1 premisszája átfogalmazható:
   "Julcsi nem a Kossuth Általános Iskolába jár vagy Julcsi nem az 1.a osztályba jár."
Jegyezzük meg, hogy a fenti kijelentésben megengedő vagy szerepel, vagyis lehetséges, hogy Julcsi nem a Kossuth Általános Iskola tanulója és nem is az 1.a osztályba jár.

(f) (láncszabály)
P1 ⇋ A⊆B
P2 ⇋ B⊆C
Q = A⊆C

A feladatban felhasznált következtetési séma: láncszabály⇒

Egy lehetséges megoldás:
Bori és Julcsi nagyon szeretik a matematikát. (P1)
Azok a tanulók, akik szeretik a matematikát, az 1.a osztályba járnak. (P2)
Bori és Julcsi az 1.a osztályba járnak. (Q)
(g) (ekvivalencia kifejezése)
P1 ⇋ A⊆B
P2 ⇋ B⊆A
Q = (A=B)

A feladatban felhasznált következtetési séma: az ekvivalencia kifejezése az implikáció segítségével.⇒

Egy lehetséges megoldás:
Azok a tanulók, akik szeretik a matematikát, az 1.a osztályba járnak. (P1)
Azok a tanulók, akik az 1.a osztályba járnak, szeretik a matematikát. (P2)
Azok a tanulók, akik szeretik a matematikát, és azok a tanulók, akik az 1.a osztályba járnak, ugyanazok. (Q)
(h) (esetelemzés)
P1 ⇋ A⊆C
P2 ⇋ B⊆C
Q = (A∪B)⊆C

A feladatban felhasznált következtetési séma: az esetelemzés szabálya⇒

Egy lehetséges megoldás:
Azok a tanulók, akik szeretik a matematikát, az 1.a osztályba járnak. (P1)
Azok a tanulók, akik szeretik az éneket, az 1.a osztályba járnak. (P2)
Azok a tanulók, akik szeretik a matematikát vagy szeretik az éneket, az 1.a osztályba járnak. (Q)
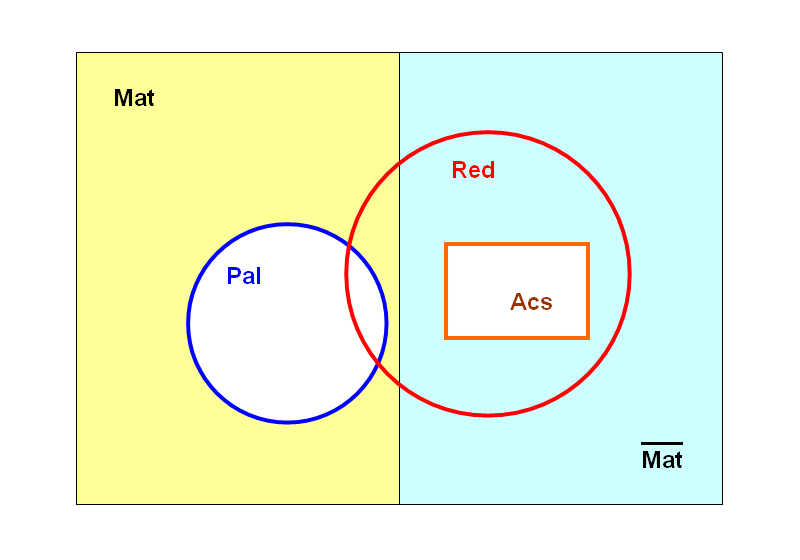
(i) (reductio ad absurdum)
Vezessük be az alábbi halmazokat:
  • A ⇋ "az osztály tanulói"
  • Pal ⇋ "a Pál utcai fiúk"
  • Red ⇋ "a Vörösingesek"
  • Mat ⇋ "azok a tanulók, akik szeretik a matematikát"
  • Acs ⇋ "Ács Feriék"
Venn-diagram: A Pál utcai fiúk és a Vörösingesek osztálya
P1 ⇋ A=Pal∪Red
P2 ⇋ Pal⊆Mat
P3 ⇋ Acs⊆Mat
Q = Acs⊆Red

A feladatban felhasznált következtetési séma: az ellentmondásra való visszavezetés (reductio ad absurdum, második variáció)⇒

Egy lehetséges megoldás:
Az osztályba a Pál utcai fiúk és a Vörösingesek járnak. (P1)
Ács Feriék ebbe az osztályba járnak. (P11)
A Pál utcai fiúk szeretik a matematikát. (P2)
Ács Feriék nem szeretik a matematikát. (P3)
Ács Feriék Vörösingesek. (Q)

Egy érdekesség: ha Geréb mind a Pál utcai fiúkhoz, mind a Vörösingesekhez tartozik, találtunk egy olyan Vörösingest, aki nem Ács Feriékhez tartozik, és szereti a matematikát.

Vegyük észre, hogy a megoldás első mondatában az és kötőszó logikai vagy értelemben szerepel. Átfogalmazva:
P1 ⇋ "Az osztály tanulói vagy Pál utcai fiúk, vagy Vörösingesek."
Jegyezzük meg, hogy azt, hogy egy mondatban megengedő vagy kizáró vagy szerepel, általában csak a tágabb szövegkörnyezetből tudjuk eldönteni.

A reductio ad absurdum alapján történő levezetés a következő lépésekből áll:
Tegyük fel ("indirekt feltevés"), hogy Ács Feriék Pál utcai fiúk.
Mivel a Pál utcai fiúk szeretik a matematikát (P2), ezért (a láncszabály⇒ miatt) Ács Feriék is szeretik a matematikát.
De mivel tudjuk, hogy Ács Feriék nem szeretik a matematikát (P3), az indirekt feltevés ellentmondásra vezetett, tehát Ács Feriék nem lehetnek Pál utcai fiúk.
Mivel az osztályba a Pál utcai fiúk és a Vörösingesek járnak (P1), továbbá Ács Feriék ebbe az osztályba járnak (P11), és Ács Feriék nem Pál utcai fiúk, ezért (a modus tollendo ponens⇒ séma miatt) Ács Feriék Vörösingesek (Q).

7.6. Példák a következtetési sémák matematikai logikai alkalmazására (kiegészítő anyag)

A következtetési sémák felhasználhatók a korábban tanult logikai azonosságok⇒ levezetésére is.

1. példa: Vezessük le az abszorpció két azonosságát:⇒

(1.1) Bizonyítsuk be, hogy ⊨ A∧(A∨B)⊃.A teljesül.

Mivel a szűkítés szabálya szerint A∧(A∨B)⊨A teljesül, ezért ⊨ A∧(A∨B)⊃.A fennáll.

(1.2) Bizonyítsuk be, hogy ⊨ A⊃.A∧(A∨B) teljesül.

Mivel A⊨A (azonosság törvénye) és A⊨(A∨B) (bővítés szabálya) teljesül, ezért az esetegyesítés szabálya⇒ miatt A⊨A∧(A∨B) teljesül. Emiatt ⊨ A⊃.A∧(A∨B) fennáll.

(1.1-2) Mivel mind ⊨ A∧(A∨B)⊃.A mind ⊨ A⊃.A∧(A∨B) teljesül, ezért az ekvivalencia műveletére vonatkozó korábban megismert azonosság miatt⇒ ⊨ A∧(A∨B)≡.A is teljesül, vagyis fennáll az abszorpció A∧(A∨B) = A azonossága. Jegyezzük meg, hogy ezt korábban értéktáblázattal is megmutattuk.⇒

(1.3) Bizonyítsuk be, hogy ⊨ A∨(A∧B)⊃.A teljesül.

Mivel A⊨A (azonosság törvénye) és (A∧B)⊨A (szűkítés szabálya) teljesül, ezért az esetelemzés szabálya⇒ miatt A∨(A∧B)⊨A teljesül. Emiatt ⊨ A∨(A∧B)⊃.A fennáll.

(1.4) Bizonyítsuk be, hogy ⊨ A⊃.A∨(A∧B) teljesül.

Mivel a bővítés szabálya szerint A⊨A∨(A∧B) teljesül, ezért ⊨ A∨(A∧B)⊃.A fennáll.

(1.3-4) Mivel mind ⊨ A∨(A∧B)⊃.A mind ⊨ A⊃.A∨(A∧B) teljesül, ezért az ekvivalencia műveletére vonatkozó korábban megismert azonosság miatt⇒ ⊨ A∨(A∧B)≡.A is teljesül, vagyis fennáll az abszorpció A∨(A∧B) = A azonossága.

2. példa: Vezessük le a disztributivitás második azonosságát⇒, amely a diszjunkció disztributivitását fejezi ki (vö. Dragálin-Buzási 1986: 129-131):

(2.1) Bizonyítsuk be, hogy ⊨ A∨(B∧C)⊃.(A∨B)∧(A∨C) teljesül.

(i) A következtetés premisszájában egy diszjunktív kifejezés szerepel. Először vizsgáljuk meg a kifejezés első tagját (A). Erre a bővítés szabálya szerint A⊨(A∨B) és A⊨(A∨C) teljesül. Ezért az esetegyesítés szabálya miatt A⊨(A∨B)∧(A∨C) teljesül.
(ii) Ezután vizsgáljuk meg a következtetés premisszájában szereplő diszjunktív kifejezés második tagját (B∧C). Erre a szűkítés szabálya szerint (B∧C)⊨B és (B∧C)⊨C teljesül. A bővítés szabálya miatt egyrészt B⊨(A∨B) másrészt C⊨(A∨C) teljesül. A láncszabály⇒ miatt tehát (B∧C)⊨(A∨B) és (B∧C)⊨(A∨C) teljesül. Ezért az esetegyesítés szabálya miatt (B∧C)⊨(A∨B)∧(A∨C) teljesül.
(iii) Mivel a bizonyítandó következtetés premisszájában szereplő diszjunktív kifejezés (azaz az A∨(B∧C) kifejezés) mindkét tagjának következménye a bizonyítandó következtetés jobb oldalán szereplő kifejezés (azaz az (A∨B)∧(A∨C) kifejezés), ezért az esetelemzés szabálya miatt ⊨ A∨(B∧C)⊃.(A∨B)∧(A∨C) fennáll.

(2.2) Bizonyítsuk be, hogy ⊨ (A∨B)∧(A∨C)⊃.A∨(B∧C) teljesül.

(i) A bizonyítandó állítás bal oldalán szereplő (A∨B)∧(A∨C) kifejezésre alkalmazhatjuk a konjunkció disztributivitását.⇒ Ekkor
X=(A∧A) ∨ (A∧B) ∨ (B∧A) ∨ (B∧C)
adódik. Ezt a kifejezést fogjuk felhasználni a bizonyításban. Először bizonyítjuk, hogy (A∨B)∧(A∨C)⊃X teljesül, majd pedig azt, hogy X⊃.A∨(B∧C) teljesül.
(ii) A konjunktív esetelemzés szabályának általánosítását⇒ alkalmazva
(A∧A⊃X) ∧ (A∧C⊃X) ∧ (B∧A⊃X) ∧ (B∧C⊃X) ⊨ (A∨B)∧(A∨C)⊃X
adódik. Ezzel
(A∨B)∧(A∨C)⊃X
bizonyítását visszavezettük
(A∧A⊃X) ∧ (A∧C⊃X) ∧ (B∧A⊃X) ∧ (B∧C⊃X)
igazolására. Mivel
→ (A∧A)⊨(A∧A) ∨ (A∧B) ∨ (B∧A) ∨ (B∧C) (bővítés szabálya), ezért ⊨(A∧A)⊃X;
→ (A∧C)⊨A (szűkítés szabálya) és A⊨(A∧A) (azonosság törvénye és esetegyesítés), továbbá (A∧A)⊨X (előző eset), ezért a láncszabály miatt ⊨(A∧C)⊃X;
→ (B∧A)⊨(A∧A) ∨ (A∧B) ∨ (B∧A) ∨ (B∧C) (bővítés szabálya), ezért ⊨(B∧A)⊃X;
→ (B∧C)⊨(A∧A) ∨ (A∧B) ∨ (B∧A) ∨ (B∧C) (bővítés szabálya), ezért ⊨(B∧C)⊃X
teljesül, ezért az esetegyesítés szabálya⇒ miatt
⊨ (A∧A⊃X) ∧ (A∧C⊃X) ∧ (B∧A⊃X) ∧ (B∧C⊃X)
szinten teljesül. Ez éppen a konjunktív esetelemzés általánosított szabályának premisszája, ami maga után vonja a szabály
⊨ (A∨B)∧(A∨C)⊃X
konklúziójának teljesülését.
(iii) Ezután bizonyítsuk be, hogy
⊨ X⊃.A∨(B∧C)
teljesül. Mivel
X=(A∧A) ∨ (A∧B) ∨ (B∧A) ∨ (B∧C) diszjunktív kifejezés, ezért alkalmazhatjuk az esetelemzés szabályát
(A∧A)⊃.A∨(B∧C), (A∧B)⊃.A∨(B∧C), (B∧A)⊃.A∨(B∧C), (B∧C)⊃.A∨(B∧C) ⊨ X⊃.A∨(B∧C)
módon. Mivel pedig
→ (A∧A)⊨A (szűkítés szabálya) és A⊨A∨(B∧C) (bővítés szabálya), ezért ⊨(A∧A)⊃.A∨(B∧C);
→ (A∧B)⊨A (szűkítés szabálya) és A⊨A∨(B∧C) (bővítés szabálya), ezért ⊨(A∧B)⊃.A∨(B∧C);
→ (B∧A)⊨A (szűkítés szabálya) és A⊨A∨(B∧C) (bővítés szabálya), ezért ⊨(B∧A)⊃.A∨(B∧C);
→ (B∧C)⊨A∨(B∧C) (bővítés szabálya), ezért ⊨(B∧C)⊃.A∨(B∧C)
teljesül, ezért
⊨ X⊃.A∨(B∧C)
szintén teljesül.
(iv) Mivel egyrészt ⊨(A∨B)∧(A∨C)⊃.X másrészt ⊨ X⊃.A∨(B∧C) teljesül, ezért a láncszabály alapján ⊨(A∨B)∧(A∨C)⊃.A∨(B∧C) teljesül.

(2.1-2) Mivel mind ⊨ A∨(B∧C)⊃.(A∨B)∧(A∨C) mind ⊨ (A∨B)∧(A∨C)⊃.A∨(B∧C) teljesül, ezért az ekvivalencia műveletére vonatkozó korábban megismert azonosság miatt⇒ ⊨ A∨(B∧C)≡.(A∨B)∧(A∨C) is teljesül, vagyis fennáll a disztributivitás A∨(B∧C) = (A∨B)∧(A∨C) azonossága.

Gyakorló feladatok

(→ következő témakörök)

Boda István, 2021-24.