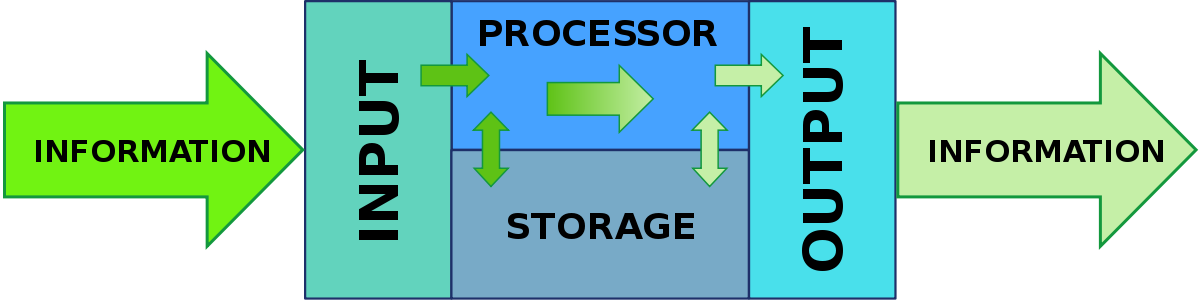
A számítógép mint fekete doboz működését leegyszerűsítve a következőképpen tudjuk megfogalmazni:
- ha bemenetként (inputként) 'n' darab bináris értéket adunk meg, akkor
- a számítógép ezekhez az értékekhez a működés algoritmusa által meghatározott módon
- kimenetként (outputként) 'm' darab bináris értéket rendel hozzá.
Formálisan ezt az alábbi 'f' függvénnyel tudjuk leírni:
f(x1,x2,...,xn) :
G1Χ
G2Χ
...Χ
Gn
→
H1Χ
H2Χ
...Χ
Hm
ahol
– Gi={0,1} (1≤i≤n) azokat a bináris értékeket tartalmazó halmazokat jelöli, amelyekből az input értékeket vesszük,
– Hj={0,1} (1≤j≤m) pedig azokat a bináris értékeket tartalmazó halmazokat jelöli, amelyekből a számítógép az output értékeket előállítja.
A fenti 'f' függvény megadása ekvivalens az alábbi 'm' darab függvény megadásával:
f1(x1,x2,...,xn) :
G1Χ
G2Χ
...Χ
Gn
→
H1
f2(x1,x2,...,xn) :
G1Χ
G2Χ
...Χ
Gn
→
H2
...
fm(x1,x2,...,xn) :
G1Χ
G2Χ
...Χ
Gn
→
Hm
ahol Gi={0,1} (1≤i≤n) és Hj={0,1} (1≤j≤m) az egyes fk (1≤k≤m) függvények értelmezési tartományát, ill. értékkészletét megadó kétértékű halmazok.
Jegyezzük meg, hogy a számítógép működését leíró 'f' függvény értéke (azaz az 'f' függvényt megadó algoritmus kimenete) függhet azoktól az értékektől is, amelyeket a számítógép korábbi működése során előállított és/vagy eltárolt (például adatbázisokat használó alkalmazások esetében nyilvánvalóan ez a helyzet; de a számítógép korábbi állapotai is meghatározhatják a számítógép működését, pl. tanuló neurális hálózatok esetén).
Erre a kérdésre később még visszatérünk, de egyelőre az egyszerűség kedvéért tételezzük fel, hogy az 'f' függvény független változói (azaz a számítógép bemenetei) teljes mértékben meghatározzák a függvény értékét. Ezt úgy is megfogalmazhatjuk, hogy nincsenek olyan "rejtett paraméterek", amelyek egyfajta formális "emlékezetként" befolyásolnák az 'f' függvény értékét (azaz a számítógép által szolgáltatott kimenetet).
Az, hogy a függvényekben a bemenetet és a kimenetet bináris értékek segítségével adtuk meg, nem jelent semmilyen korlátozást a számítógép működésére nézve. Korábban láttuk, hogy lényegében bármilyen típusú adat, például a
számok,⇒
vagy a
karakterek, ill. szöveges adatok⇒
ábrázolhatók bináris értékek meghatározott sorozatával.
A számítógép működésének leírásakor használt {0,1} bináris értékeket egyaránt tekinthetjük
– bináris számjegyeknek,
– logikai értékeknek (például 0↔'hamis', 1↔'igaz' értelemben), ill.
– egy digitális áramkör feszültségszintjeinek (például 0↔'alacsony feszültségszint', 1↔'magas feszültségszint' értelemben).
Ha a {0,1} bináris értékeket logikai értékeknek tekintjük (0↔'hamis', 1↔'igaz' értelemben), akkor a számítógép működését 'n' változós
p1(x1,x2,...,xn):{0,1}Χ{0,1}Χ...Χ{0,1}→{0,1}
...
pk(x1,x2,...,xn):{0,1}Χ{0,1}Χ...Χ{0,1}→{0,1}
...
pm(x1,x2,...,xn):{0,1}Χ{0,1}Χ...Χ{0,1}→{0,1}
alakú logikai függvények segítségével írhatjuk le, ahol az xi argumentumok (1≤i≤n) kétértékű (vagyis 'igaz' vagy 'hamis' értékű) logikai változók (1≤k≤m, 'm' tetszőleges pozitív egész szám).
Először azzal a kérdéssel foglalkozunk, hogyan tudunk ilyen logikai függvényeket előállítani, utána pedig azt vizsgáljuk meg, milyen eszközök állnak rendelkezésünkre, hogy ezeket a logikai függvényeket technikailag is megvalósítsuk, és egy működőképes (elektronikus) rendszert állítsunk elő.
A továbbiakban bevezetünk három logikai alapműveletet, amelyek segítségével bármilyen logikai függvény előállítható. A digitális számítógépek működésének alapja, hogy a logikai alapműveletek (és ezáltal a logikai függvények) technikailag megvalósíthatók digitális áramkörök, ún. kapuáramkörök segítségével.
A három logikai alapművelet a következő:
- negáció (tagadás, logikai "nem")
- konjunkció (logikai "és")
- diszjunkció (logikai "vagy")
A továbbiakban jelöljük a logikai változókat A, B, C, ...-vel.
Jegyezzük meg, hogy a logikai változók csak két értéket vehetnek fel, a 0 ("hamis") vagy az 1 ("igaz") értékeket.
Egyes esetekben szükségünk lesz még két logikai konstansra is: azt a szimbólumot, amely mindig igaz, ⊤ módon (ún. "szabvány igaz"), azt a szimbólumot pedig, amely mindig hamis, ⊥ módon (ún. "szabvány hamis") fogjuk jelölni.
A logikai alapműveletek egyváltozós és kétváltozós logikai függvények. Ezért a logikai műveleteket legegyszerűbben ún. igazságtáblázatokkal tudjuk leírni, amelyben az értelmezési tartomány minden lehetséges értékéhez megadjuk az értékkészlet megfelelő elemét.
(1) negáció vagy tagadás ("nem A" vagy "NOT A"; jele ⌝A, de szokásos az A jelölés is)
A negáció
⌝A:{0,1}→{0,1}
módon leírható egyváltozós logikai függvény. Igazságtáblázata a következő:
(2) konjunkció vagy logikai "és" ("A és B", "A AND B"; jele: A∧B, de szokásos egyszerűen az AB jelölés is)
A konjunkció
A∧B:{0,1}Χ{0,1}→{0,1}
módon leírható kétváltozós logikai függvény. Igazságtáblázata a következő:
konjunkció
| A
| B
| ( A ∧ B )
|
| 0
| 0
| 0
|
| 0
| 1
| 0
|
| 1
| 0
| 0
|
| 1
| 1
| 1
|
(3) diszjunkció vagy logikai (megengedő) "vagy" ("A vagy B", "A OR B"; jele: A∨B, de szokásos az A+B jelölés is)
A diszjunkció
A∨B:{0,1}Χ{0,1}→{0,1}
módon leírható kétváltozós logikai függvény. Igazságtáblázata a következő:
diszjunkció
| A
| B
| ( A ∨ B )
|
| 0
| 0
| 0
|
| 0
| 1
| 1
|
| 1
| 0
| 1
|
| 1
| 1
| 1
|
A három alapvető logikai művelet igazságtáblázatai alapján könnyen ellenőrizhetők a logikai alapműveletek alapvető tulajdonságait leíró alábbi logikai azonosságok, más néven logikai törvények:
A logikai alapműveletekkel kifejezhető legfontosabb azonosságok:
- kettős tagadás: ⌝(⌝A) = A
- a konjunkció idempotenciája: A∧A = A
-
a konjunkció kommutativitása: A∧B = B∧A
- a konjunkció asszociativitása: (A∧B)∧C = A∧(B∧C)
- konjunkció szabványkijelentésekkel:
- a diszjunkció idempotenciája: A∨A = A
-
a diszjunkció kommutativitása: A∨B = B∨A
- a diszjunkció asszociativitása: (A∨B)∨C = A∨(B∨C)
- diszjunkció szabványkijelentésekkel:
- disztributivitás:
- A∧(B∨C) = (A∧B)∨(A∧C)
- (A∨B)∧(C∨D)
=
(A∧C)∨(A∧D)∨(B∧C)∨(B∧D)
- A∨(B∧C) = (A∨B)∧(A∨C)
- (A∧B)∨(C∧D)
=
(A∨C)∧(A∨D)∧(B∨C)∧(B∨D)
-
abszorpció (elnyelés; elimináció):
- A∧(A∨B) = A
- A∨(A∧B) = A
- (A∧B)∨(A∧B∧C)
=
(A∧B)
- (A∧C)∨(B∧⌝C)∨(A∧B) = (A∧C)∨(B∧⌝C)
-
de Morgan-féle azonosságok:
- ⌝(A∧B) = ⌝A∨⌝B
- ⌝(A∨B) = ⌝A∧⌝B
-
felbontás:
Logikai alapelvek:
- az ellentmondás törvénye:
- a kizárt harmadik törvénye:
A fenti logikai azonosságokban (vagy tautológiákban) használt "kiemelt" egyenlőségjel ( = ) az általa összekapcsolt logikai kifejezések ekvivalenciáját fejezi ki:
a logikai azonosságokban az egyenlőségjel bal- és jobboldalán szereplő logikai kifejezések a bennük szereplő logikai változók minden lehetséges értéke mellett azonos logikai értéket adnak.
(A logikai kifejezések ekvivalenciájának jelölésére szokásos az
A~B
jelölés is.)
A logikai azonosságok bal- és jobboldalán ekvivalens logikai kifejezések szerepelnek. Ezért ha egy tetszőleges 'p' logikai kifejezést úgy alakítunk át, hogy egy benne szereplő 'a' logikai kifejezést az a~b logikai azonosság felhasználásával egy vele ekvivalens 'b' kifejezéssel helyettesítünk, a 'p' logikai kifejezéssel ekvivalens 'q' logikai kifejezést kapunk. Ilyenkor p~q miatt ekvivalens átalakításról vagy azonos átalakításról beszélünk.
A fenti logikai azonosságok bármelyike könnyen igazolható igazságtáblázatok létrehozásával. Például igazoljuk az abszorpció törvényét, azaz az
A∧(A∨B) = A
azonosságot egy igazságtáblázattal:
A táblázatból leolvasható, hogy az abszorpciót kifejező azonosság bal- és jobboldalán szereplő logikai kifejezések értékei az 'A' és 'B' kijelentésváltozók minden lehetséges értéke mellett megegyeznek, vagyis az azonosság teljesül. Vegyük észre, hogy ez megfelel annak, hogy az
A∧(A∨B) ≡. A
ekvivalencia az 'A' és 'B' kijelentésváltozók minden lehetséges értékére igaz, vagyis
⊨ A∧(A∨B) ≡. A
logikai törvény (ill. tautológia).
Az igazságtáblázatokat könnyen és kényelmesen létrehozhatjuk JavaScript programok segítségével is.⇒
A JavasScript programok legegyszerűbben a már korábban használt online JavaScript interpreter⇒ segítségével futtathatók.
Példa: írassuk ki a negáció (⌝A), a konjunkció (A∧B), és a diszjunkció (A∨B) igazságtáblázatát!
A negáció (⌝A) igazságtáblázata:
// negáció igazságtáblázata
function neg(x) {
var a=Boolean(x);
var c=!a;
return Number(c);
}
writeln("A"+" "+"⌝A");
writeln("-----");
for(i=0;i<=1;i++) {
var k=neg(i);
writeln(i+" "+k);
}
writeln("-----");
A konjunkció (A∧B) igazságtáblázata:
// konjunkció igazságtáblázata (saját függvény létrehozásával)
function kon(x,y) {
var a=Boolean(x), b=Boolean(y);
var c=a && b;
return Number(c);
}
writeln("A"+" " +"B"+" "+"A∧B");
writeln("-------");
for(i=0;i<=1;i++) {
for(j=0;j<=1;j++) {
var k=kon(i,j);
writeln(i+" " +j+" "+k);
}
}
writeln("-------");
A diszjunkció (A∨B) igazságtáblázata:
// diszjunkció igazságtáblázata
function disz(x,y) {
var a=Boolean(x), b=Boolean(y);
var c=a || b;
return Number(c);
}
writeln("A"+" " +"B"+" "+"A∨B");
writeln("-------");
for(i=0;i<=1;i++) {
for(j=0;j<=1;j++) {
var k=disz(i,j);
writeln(i+" " +j+" "+k);
}
}
writeln("-------");
A logikai azonosságok felhasználásával lehetőségünk van arra, hogy különböző logikai kifejezéseken ekvivalens átalakításokat hajtsunk végre (például azért, hogy egyszerűbb alakra hozzuk őket). Próbáljuk meg egyszerűsíteni például a p(A,B,C) három változós logikai kifejezést, felhasználva a konjunkció disztributivitását, a harmadik kizárásának logikai törvényét és a konjunkció szabvány igaz kijelentés mellett érvényes azonosságát:
p(A,B,C) =
(⌝A∧B∧⌝C) ∨
(⌝A∧B∧C) =
(⌝A∧B) ∧
(⌝C∨C) =
(⌝A∧B) ∧
⊤ =
(⌝A∧B)
Általánosan megfogalmazva a fenti levezetés eredményét: azt mondhatjuk, hogy ha diszjunkcióval (∨) összekapcsolunk két olyan konjunktív (csak ∧ műveletet tartalmazó) kifejezést, amelyek azonos változókat (A, B és C) tartalmaznak, és csak egy változó ponált (C), illetve negált (⌝C) alakjában különböznek (vagyis A és B a konjunktív kifejezésekben azonos alakban szerepelnek), akkor a konjunktív kifejezéseket megkülönböztető változó (azaz C) egyszerűen elhagyható.
A logikai alapműveletek (∧, ∨ és ⌝) mellett három további logikai műveletet érdemes megismerni. Ezek a kizáró vagy, az implikáció és az ekvivalencia.
(4) kizáró vagy ("A XOR B", jele: A⨁B)
A kizáró vagy
A⨁B:{0,1}Χ{0,1}→{0,1}
módon leírható kétváltozós logikai függvény. Igazságtáblázata a következő:
kizáró vagy
| A
| B
| ( A ⨁ B )
|
| 0
| 0
| 0
|
| 0
| 1
| 1
|
| 1
| 0
| 1
|
| 1
| 1
| 0
|
A kizáró vagy műveletet az
A⨁B = (A∨B)∧⌝(A∧B)
vagy az
A⨁B = (A∧⌝B)∨(⌝A∧B)
azonosságokkal vissza tudjuk vezetni a korábban megismert logikai alapműveletekre.
(5) implikáció ("...-ból következik", jele: A⊃B, de előfordul az A⇒B jelölés is)
Az implikáció
A⊃B:{0,1}Χ{0,1}→{0,1}
módon leírható kétváltozós logikai függvény. Igazságtáblázata a következő:
implikáció
| A
| B
| ( A ⊃ B )
|
| 0
| 0
| 1
|
| 0
| 1
| 1
|
| 1
| 0
| 0
|
| 1
| 1
| 1
|
Az implikációt az
A⊃B = ⌝A∨B
azonossággal vissza tudjuk vezetni a korábban megismert logikai alapműveletekre.
(6) ekvivalencia ("ekvivalens", jele: A≡B, de előfordul az A⇔B jelölés is)
Az ekvivalencia
A≡B:{0,1}Χ{0,1}→{0,1}
módon leírható kétváltozós logikai függvény. Igazságtáblázata a következő:
ekvivalencia
| A
| B
| ( A ≡ B )
|
| 0
| 0
| 1
|
| 0
| 1
| 0
|
| 1
| 0
| 0
|
| 1
| 1
| 1
|
Az ekvivalenciát az
A≡B = (A⊃B)∧(B⊃A)
az
A≡B = ⌝(A⨁B)
vagy az
A≡B = (A∧B)∨(⌝A∧⌝B)
azonosságokkal vissza tudjuk vezetni a korábban megismert logikai alapműveletekre.
Végezetül jegyezzük meg, hogy az igazságértékeket tartalmazó H={0,1} alaphalmaz a fenti tulajdonságokkal rendelkező három logikai alapművelettel ún. Boole-algebrát alkot. (A (H; ∧, ∨) disztributív háló zéruseleme a ⊥ szabvány-hamis elem, egységeleme a ⊤ szabvány-igaz elem; a 0 elem tagadása ("komplementuma") az 1 elem, az 1 elem tagadása pedig a 0 elem.)
Gyakorló feladatok
Igazolja értéktáblázattal és azonos átalakítások segítségével az alábbi logikai azonosságokat, ill. törvényeket!
Írassa ki a logikai kifejezések értéktáblázatát JavaScript programok segítségével is!⇒
Jelölések:
(1) Ha egy 'p' formula "azonosan igaz", vagyis tautológia, ill. logikai törvény, ezt
⊨ p
módon jelöljük. Ha a 'p' formula logikai törvény, akkor
p = ⊤
teljesül.
(2) Ha egy művelet után a '.' (pont) operátor szerepel, akkor az adott kifejezésben a ponttal jelölt műveletet utoljára kell végrehajtani. A pont operátor mindig helyettesíthető a kijelölt művelet elé és után írt zárójelekkel. Ennek megfelelően például a
q∧r∨.p∧q
kifejezés ekvivalens a
(q∧r)∨(p∧q)
kifejezéssel.
(3) A kizáró vagy műveletét (A⨁B) helyettesíthetjük a vele ekvivalens
(A∧⌝B)∨(⌝A∧B)
kifejezéssel.⇒
(4) Az implikáció műveletét (A⊃B) helyettesíthetjük a vele ekvivalens
⌝A∨B
kifejezéssel.⇒
(4) Az ekvivalencia műveletét (A≡B) szintén helyettesíthetjük a vele ekvivalens
(A∧B)∨(⌝A∧⌝B)
kifejezéssel.⇒
(a) p∧(p⊃q) = p∧q
Induljunk ki a bizonyítandó azonosság bal oldalából. Célunk az, hogy a korábbi logikai azonosságokat⇒ felhasználva olyan azonos átalakításokat végezzünk, amelynek végén eljutunk a bizonyítandó azonosság jobb oldalán szereplő logikai kifejezéshez:
p∧(p⊃q) = (implikáció helyettesítése)
p∧(⌝p∨q) =
(p∧⌝p)∨(p∧q) =
⊥∨(p∧q) =
p∧q (q.e.d)
(b) ⌝p∨(p∧q) = p⊃q
(c) q⊃(p∧q) = q⊃p
(d) p∧(⌝p⊃q) = p
(e) p∨⌝(p⊃q) = p
(f) (p⊃q)⊃p = p
(g) ⊨ ⌝p⊃(p⊃q)
(ennek a logikai törvénynek a jelentése az, hogy "az ellentmondásból bármi következik", vö. Dragálin-Buzási 1986: 88)
Induljunk ki a bizonyítandó logikai törvényből. Célunk az, hogy a korábbi logikai azonosságokat⇒ felhasználva olyan azonos átalakításokat végezzünk, amelynek végén eljutunk a "szabvány igaz" (⊤)⇒ kijelentéshez:
⌝p⊃(p⊃q) = (→ implikáció kifejezése)
⌝p⊃(⌝p∨q) = (→ implikáció kifejezése)
⌝⌝p∨(⌝p∨q) = (→ kettős tagadás)
p∨(⌝p∨q) = (→ asszociativitás)
(p∨⌝p)∨q = (→ kizárt harmadik törvénye⇒)
⊤∨q = (→ diszjunkció szabvány-igaz kijelentéssel)
⊤ (q.e.d.)
(h) ⊨ p⊃(q⊃p)
(i) ⊨ p⊃(q⊃.p∧q)
(j) ⊨ p∧(p⊃q)⊃.q
(k) ⊨ (p⊃q)∧⌝q⊃.⌝p
(l) A⨁B⨁C
=
(⌝A∧B∧⌝C) ∨ (A∧⌝B∧⌝C) ∨
(⌝A∧⌝B∧C) ∨
(A∧B∧C)
(A fenti kifejezés az egybites teljes összeadó⇒ által szolgáltatott összeget adja meg.)
(m) (A∧B∧C) ∨
(⌝A∧B∧C) ∨
(A∧⌝B∧C) ∨
(A∧B∧⌝C)
=
(A∧B) ∨ (A∧C) ∨ (B∧C)
(A fenti kifejezés az egybites teljes összeadó⇒ által szolgáltatott átvitelt adja meg.)
(Megjegyzés: mivel az egyszerűsítendő kifejezés t.d.n.f. alakban⇒ van, a levezetés a Karnaugh-tábla⇒ alapján könnyen megkapható.⇒)
(n) (A∧C) ∨ (B∧⌝C) ∨ (A∧B)
=
(A∧C) ∨ (B∧⌝C)
Használjuk fel a felbontás⇒ azonosságát, majd alkalmazzuk kétszer az abszorpció⇒ azonosságát:
(A∧C) ∨ (B∧⌝C) ∨ (A∧B)=
(A∧C) ∨ (B∧⌝C) ∨ (A∧B∧C) ∨ (A∧B∧⌝C)=
(A∧C) ∨ (A∧C∧B)
∨
(B∧⌝C) ∨ (B∧⌝C∧A)=
(A∧C) ∨ (B∧⌝C)
(q.e.d.)
(o) ⊨ A≡B ⊃. (A⊃B)∧(B⊃A)
Induljunk ki a bizonyítandó logikai törvényből. Célunk most is az, hogy a korábbi logikai azonosságokat⇒ felhasználva olyan azonos átalakításokat végezzünk, amelynek végén eljutunk a "szabvány igaz" (⊤)⇒ kijelentéshez:
A≡B ⊃. (A⊃B)∧(B⊃A)
=
(A∧B)∨(⌝A∧⌝B) ⊃. (A⊃B)∧(B⊃A)
=
(A∧B)∨(⌝A∧⌝B) ⊃. (⌝A∨B)∧(⌝B∨A)
=
⌝[(A∧B)∨(⌝A∧⌝B)] ∨. (⌝A∨B)∧(⌝B∨A)
=
⌝(A∧B)∧⌝(⌝A∧⌝B) ∨. (⌝A∨B)∧(⌝B∨A)
=
(⌝A∨⌝B)∧(⌝⌝A∨⌝⌝B) ∨. (⌝A∨B)∧(⌝B∨A)
=
(⌝A∨⌝B)∧(A∨B) ∨. (⌝A∨B)∧(⌝B∨A)
=
az ∨. operátor mindkét oldalán alkalmazzuk a disztributivitás⇒ azonosságát:
(⌝A∧A)∨(⌝A∧B)∨(⌝B∧A)∨(⌝B∧B)
∨.
(⌝A∧⌝B)∨(⌝A∧A)∨(B∧⌝B)∨(B∧A)
=
(⌝A∧B)∨(⌝B∧A)∨(⌝A∧⌝B)∨(B∧A)
=
(⌝A∧B)∨(⌝A∧⌝B)
∨.
(⌝B∧A)∨(B∧A)
=
(⌝A∧B)∨(⌝A∧⌝B)
∨.
(⌝B∧A)∨(B∧A)
=
⌝A∧(B∨⌝B)
∨.
(⌝B∨B)∧A
=
⌝A∨A
=
⊤ (q.e.d.)
→ További feladatok