Alkalmazott matematika 1

Tartalom, témakörök

7. Elemi vektoralgebra. Vektoriális és vegyes szorzat^⇒ (Selényi-Szendrei 1969: 95-133; Farkas-Farkasné 2001: 7-35)
8. Trigonometrikus függvények^⇒ (Obádovics 1972: 364-437; Farkas-Fritzné-Kissné 2000: 21-29; Czinder 2021)
9. Az analitikus geometria alapjai^⇒ (Selényi-Szendrei 1969: 157-186; Obádovics 1972: 447-468; Reiman 1992: 326-343, 371-381)
10. Kör, parabola, ellipszis, hiperbola. Kúpszeletek és másodrendű görbék^⇒ (Reiman 1992: 345-371; Obádovics 1972: 468-515; Selényi-Szendrei 1969: 210-289)
11.  előző témakörök (1−6) ⇒ 

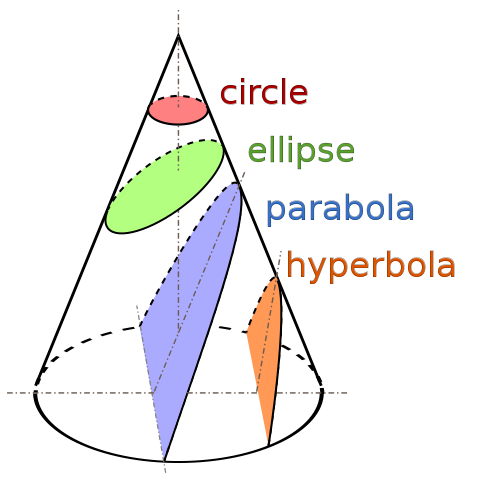
7.1. Elemi vektoralgebra

A továbbiakban a vektorok tulajdonságait fogjuk vizsgálni a három dimenziós térben, a "középiskolai tanulmányaink során megszokott s tapasztalt teret" alapul véve (Selényi-Szendrei 1969: 95). Egyes esetekben a vektorok tulajdonságait a két dimenziós síkban fogjuk vizsgálni.

A tér egy irányított szakasza a tér két pontját (P₁ és P₂) a megadott sorrendben összekötő egyenes szakasz. Jelöljük ezt az irányított szakaszt P₁P₂ módon.

Egy P₁P₂ irányított szakaszhoz a következő jellemzők tartoznak:

• az irányított szakasz kezdőpontja (P₁);
• az irányított szakasz végpontja (P₂);
• az irányított szakasz iránya (P₁→P₂);
• az irányított szakasz állása (a P₁ és P₂ pontokon átmenő egyenes);
  • két irányított szakasz párhuzamos, ha a szakaszok állása megegyező (azaz a szakaszok végpontjain átmenő egyenesek eltolással egymásba átvihetők);
  • a zérusvektort (nullvektort) bármely vektorral párhuzamosnak tekintjük (vö. Farkas-Farkasné 2001: 7)
• az irányított szakasz hossza.

"Világos, hogy végtelen sok olyan irányított szakasz van, amelyiknek megegyezik a hossza, az állása és az iránya; bármely két ilyen irányított szakasz közül az egyik a másikba eltolással átvihető. Az ilyen irányított szakaszok közül tetszés szerint egyet kiválasztunk, s ezt vektornak nevezzük." (Selényi-Szendrei 1969: 96)

Rögzítsünk egy Descartes-féle koordináta-rendszert az x, y és z tengelyek irányába mutató
e_x=i, e_y=j, e_z=k
egységvektorokkal. A három dimenziós térben bármely
v=(x,y,z)
vektor az origóból (O) kiinduló és a P=(x,y,z) pontba mutató irányított szakaszként fogható fel, amelynek kezdőpontja az origó, végpontja a P pont, iránya pedig az origóból a P pontba mutat (O→P).

Az i, j és k egységvektorok által alkotott természetes bázisban egy tetszőleges v vektor a
v=x*i+y*j+z*k
lineáris kombináció segítségével fejezhető ki, ahol (x,y,z) a v vektor természetes bázisra vonatkozó koordinátáit jelenti.

Legyen P₁P₂ egy tetszőleges irányított szakasz és legyen ℙ(P₁P₂) azoknak az irányított szakaszoknak a halmaza, amelyek eltolással a P₁P₂ szakaszba (és ezáltal egymásba) átvihetőek. A továbbiakban minden ℙ(P₁P₂)-beli irányított szakaszhoz ugyanazt a vektort fogjuk hozzárendelni: azt az origó kezdőpontú vektort, amely mint irányított szakasz maga is a ℙ(P₁P₂) halmazba tartozik.

• Minden vektort egyértelműen meghatározhatunk egy olyan irányított szakasszal, amelynek adott a kezdőpontja és a végpontja (és iránya ennek megfelelően a kezdőpontból a végpontba mutat).
• Egy adott v=(x,y,z) vektorhoz végtelen sok irányított szakaszt rendelhetünk hozzá; egyrészt
  • azt az irányított szakaszt, amelynek kezdőpontja az origó (O), és végpontja a vektor koordinátái által meghatározott P=(x,y,z) pont;
  • másrészt bármely olyan P₁P₂ irányított szakaszt, amely eltolással az OP irányított szakaszba vihető át (azaz a szakaszok párhuzamosak és egyirányúak).

Ezzel a hozzárendeléssel az irányított szakaszok halmazát ekvivalenciaosztályokra bontottuk úgy, az egymásba eltolható irányított szakaszokat (és csak azokat) egy ekvivalenciaosztályba soroltuk. Minden ekvivalenciaosztályban pontosan egy olyan irányított szakasz van, amelynek a kezdőpontja a koordináta-rendszer origója. Az ennek megfelelő vektort rendeljük az adott ekvivalenciaosztályhoz.

Mivel egyes fizikai alkalmazásokban (pl. a statikában az erő esetében) "az irányított szakaszok nem tolhatók el önmagukkal párhuzamosan, más szóval kezdőpontjuk egy ponthoz rögzített", jegyezzük meg, hogy a fenti módon értelmezett (vagyis "szabadon eltolható") vektorokat szabad vektoroknak, míg a kezdőponthoz rögzített vektorokat kötött vektoroknak nevezzük (vö. Selényi-Szendrei 1969: 97).

A korábbiaknak megfelelően értelmezzük

• a zérusvektort,^⇒
• két vektor mint mátrix összegét (és különbségét),^⇒
• egy vektor mint mátrix skalárral való szorzatát,^⇒
  • a vektorokkal végezhető műveletek tulajdonságait lineáris terekben,^⇒
  • a vektorok lineáris kombinációját,^⇒
• két vektor skaláris szorzatát,^⇒
  • a skaláris szorzás tulajdonságait euklideszi terekben^⇒
• egy vektor hosszát,^⇒ valamint
  • az egységvektort.^⇒

---

Nézzük meg ezek után egy egyszerű példán keresztül, hogyan jelennek meg a fenti fogalmak síkbeli vektorok esetén, a két dimenziós síkban.

Legyen a=(1,2) és b=(3,1) két síkbeli vektor. Ekkor teljesülnek az alábbiak:

• a+b = (1,2)+(3,1) = (1+3,2+1) = (4,3)
• 2*b = 2*(3,1) = (2*3,2*1) = (6,2)
• 2*b−a = (6,2)−(1,2) = (6−1,2−2) = (5,0)
• 2*b−(a+b) = b−a = (6,2)−(4,3) = (6−4,2−3) = (2,−1)
• ...
• a = 1*e_x+2*e_y
• b = 3*e_x+1*e_y
• mivel e_x=(1,0), ezért
  • a*e_x = (1,2)*(1,0) = 1*1+2*0 = 1 (az a vektor 'x' koordinátája!)
  • b*e_x = (3,1)*(1,0) = 3*1+1*0 = 3 (a b vektor 'x' koordinátája!)
• mivel e_y=(0,1), ezért
  • a*e_y = (1,2)*(0,1) = 1*0+2*1 = 2 (az a vektor 'y' koordinátája!)
  • b*e_y = (3,0)*(1,1) = 3*0+1*1 = 1 (a b vektor 'y' koordinátája!)
• |a|² = (1,2)*(1,2) = 1*1+2*2 = 5 (vagyis az a vektor hossza √5, ami az ábra alapján a Pithagorasz-tétel alkalmazásával is megkapható)
• |b|² = (3,1)*(3,1) = 3*3+1*1 = 10 (vagyis a b vektor hossza √10, ami az ábra alapján a Pithagorasz-tétel alkalmazásával is megkapható)
• a^o = a/|a| = (1,2)/√5 = (1/√5,2/√5) ≈ (0.447,0.894) (az a vektor irányába mutató egységvektor)
• b^o = b/|b| = (3,1)/√10 = (3/√10,1/√10) ≈ (0.949,0.316) (a b vektor irányába mutató egységvektor)

Az ábrán megfigyelhető a vektorok összeadására vonatkozó szabály: egy b vektort úgy adunk hozzá egy a vektorhoz, hogy
   (1) a b vektort eltoljuk úgy, hogy kezdőpontja az a vektor végpontjával essen egybe (ilyenkor azt mondjuk, hogy összefűzzük az a és b vektorokat);
   (2) az a és b vektorok összefűzése után az a+b összegvektor kezdőpontja az a vektor kezdőpontja, végpontja pedig a b vektor végpontja lesz.

"Ha a és b nem párhuzamos, akkor két vektor összegét és az összeadás kommutativitását a két vektorral mint oldallal szerkesztett paralelogramma mutatja" (Selényi-Szendrei 1969: 99). Ez az ún. paralelogramma-szabály.

Az a és b vektorok (b−a) különbsége az a vektor, amit az a vektorhoz adva a b vektort kapjuk. Ebből következően a (b−a) különbségvektort úgy kapjuk meg, hogy
(1) először is az a vektort szükség esetén eltoljuk úgy, hogy kezdőpontja azonos legyen a b vektor kezdőpontjával;
(2) ezek után a (b−a) különbségvektor kezdőpontja a kivonandó vektor (a) végpontja, végpontja pedig a kisebbítendő vektor (b) végpontja lesz.

Ha több vektort akarunk összeadni, akkor az összeadandó vektorokat egy adott sorrendben összefűzzük (az összeadás kommutativitása miatt a sorrendet tetszőlegesen választhatjuk meg). Az összegvektor kezdőpontja az első vektor kezdőpontjával, az összegvektor végpontja pedig az utolsó vektor végpontjával fog egybeesni.

Számoljuk ki ezek után az a és b vektorok skaláris szorzatát:

a*b = (1,2)*(3,1) = 1*3+2*1 = 5

Képezzük az U=[a,b] mátrixot, amelynek oszlopvektorai az a és b vektorok. Mivel az

U = 

1	3
2	1

mátrix reguláris (det U=1*1−3*2=1−6=−5), ezért az a és b vektorok lineárisan függetlenek, vagyis a síkban (egy két dimenziós lineáris térben) bázist alkotnak.

A síkban két vektor akkor lineárisan függő, ha az egyik vektor kifejezhető a másik skalárszorosaként, azaz a két vektor egy egyenesbe esik (a vektorok kollineárisak).

A 2*2-es U mátrix inverze nagyon könnyen kiszámítható,^⇒ mivel mindegyik algebrai aldeterminánsa egy 1*1-es mátrix:

U⁻¹ = −1/5* 

1	−3
−2	1

Álljon az U bázis az u₁=a és u₂=b vektorokból. Számítsuk ki a fenti példában szereplő vektorok U-bázisra vonatkozó koordinátáit az
x_U=U⁻¹*x
képlet^⇒ alapján:

	x	y	xU	yU
a	1	2	1	0
b	3	1	0	1
a+b	4	3	1	1
2*b	6	2	0	2
2*b−a	5	0	−1	2

Például az a=(a_x,a_y)=(1,2) vektor U-bázisra vonatkozó koordinátáit
a_xU = (-1/5)*(1*1-3*2) = 1
a_yU = (-1/5)*((-2)*1+1*2) = 0
módon számíthatjuk ki. (Ez abból is következik, hogy az a vektor az U bázis első bázisvektora, és emiatt a=1*a+0*b nyilvánvalóan teljesül.)
A c=a+b=(4,3) vektor esetében az U-bázisra vonatkozó koordinátákat teljesen hasonlóan,
c_xU = (-1/5)*(1*4-3*3) = (-1/5)*(-5) = 1
c_yU = (-1/5)*((-2)*4+1*3) = (-1/5)*(-5) = 1
módon kaphatjuk meg.

Számoljuk ki az U bázis bázisvektoraiból képezhető Gram-féle mátrix^⇒ elemeit:

• g₁₁ = a*a = 5
• g₁₂ = a*b = 5
• g₂₁ = b*a = 5
• g₂₂ = b*b = 10

Az U bázisban a bázisvektorokra nyilvánvalóan teljesül, hogy
    a_U=(1,0) és
    b_U=(0,1).
Ezek alapján az a*b skaláris szorzat kiszámítható az a és b vektorok U bázisra vonatkozó koordinátáinak segítségével is:

a*b = g₁₁*a_U1*b_U1 + g₁₂*a_U1*b_U2 + g₂₁*a_U2*b_U1 + g₂₂*a_U2*b_U2 = g₁₂*a_U1*b_U2 = g₁₂*1*1 = 5

7.2. Vektoriális és vegyes szorzat

Legyenek a, b, és c síkbeli vagy térbeli vektorok. "Két vektor szögén az irányukat jellemző félegyenesekkel, mint szögszárakkal meghatározott kisebbik szöget értjük." (Selényi-Szendrei 1969: 97)

Ebből következik, hogy egyirányú vektorok szöge (vagy hajlásszöge) zérus, ellentétes irányú vektorok szöge pedig egyenesszög.

A későbbiekben szükségünk lesz az alábbi fogalmakra:

(1) A szög mértékegységeként általában a radiánt (vagy ívmértéket) szokás használni. Egy α szög ívhossza (azaz a szög nagysága radiánban mint mértékegységben kifejezve) megegyezik egy egységsugarú körben (r=1) azzal az ívhosszal (b), amely az α középponti szöghöz tartozik.

Általánosan megfogalmazva: ha egy tetszőleges, 'r' sugarú körben az α középponti szöghöz a kör 'i' ívhossza tartozik, akkor
    α=i/r
teljesül.

A definícióból következően a derékszög mértéke radiánban arc 90°=π/2, az egyenesszög mértéke radiánban arc 180°=π, és a teljesszög mértéke radiánban arc 360°=2*π (ahol 'arc' a fokban kifejezett szög ívmértékét jelöli).

Helyezzük el a fenti ábrán szereplő kört egy Descartes-féle (derékszögű) koordináta-rendszerben úgy, hogy az 'α' középponti szög "alsó" szára essen egybe az 'x' tengellyel, a kör középpontja pedig az origóval. (Ebben az esetben az 'α' szöget irányszögnek szokás nevezni.)

(2) Forgassuk el a derékszögű koordináta-rendszerben az 'α' középponti szöghöz mint irányszöghöz tartozó (ún. "mozgó") szögszárat az origó körül pozitív (azaz az óramutató járásával ellentétes) vagy negatív irányban, miközben a szög másik, a koordináta-rendszer 'x' tengelyével egybeeső (ún. "nyugvó") szárát rögzítjük.

Egy teljes kör megtétele után a mozgó szögszár önmagába megy át, ilyenkor az 'α' szög mértékét 2*π értékkel növeljük, ill. csökkentjük a forgás irányától függően. Ezzel a szög mértékét tetszőleges valós szám esetén értelmezhetjük. Ilyenkor ún. forgásszögről beszélünk. (vö. Farkas-Fritzné-Kissné 2000: 21)

(3) Tegyük fel, hogy a derékszögű koordináta-rendszerben az 'α' forgásszöghöz mint középponti szöghöz tartozó ("mozgó") szögszár az egységsugarú kört a P(x,y) pontban metszi. Ekkor

• a P(x,y) pont első koordinátáját az 'α' szög koszinuszának nevezzük, azaz
  • cos(α) ⇋ x;
• a P(x,y) pont második koordinátáját az 'α' szög szinuszának nevezzük, azaz
  • sin(α) ⇋ y.

Vegyük észre, hogy a fenti ábrán szereplő 'α' hegyesszög esetén az O(0,0) pont (az origó), a P(x,y) pont és a P_x(x,0) pont (a P pont merőleges vetülete az 'x' tengelyre) egy derékszögű háromszöget határoz meg, amelynek egyik hegyesszöge α, másik hegyesszöge pedig (π/2−α) nagyságú.

Legyenek a és b síkbeli vagy térbeli vektorok. Ekkor skaláris szorzatukra a következő teljesül:

• a*b=|a|*|b|*cos(φ), ahol φ az a és b vektorok által bezárt szög.

A korábbi példában^⇒ a=(1,2) miatt a=e_x+2*e_y, vagyis a*e_x=a_x=1 teljesül. Ha az a vektornak az 'x' tengellyel (és ezáltal az e_x egységvektorral) bezárt szöge 'φ', akkor a fenti képletből
cos(φ)=a*e_x/(|a|*|e_x|)=1/|a|
következik. Ez megfelel a (0,0)-(1,2)-(1,0) derékszögű háromszögben a koszinusz függvény "hagyományos" definíciójának ("a szög melletti befogó osztva az átfogóval").^⇒

Két vektor akkor és csak akkor merőleges egymásra, ha skaláris szorzatuk zérus.

A három dimenziós térben vezessünk be két további műveletet, a vektorok vektoriális szorzatát és vegyes szorzatát.

(1) Legyenek a és b térbeli vektorok. Az a és b vektorok vektoriális szorzatán azt az a×b vektort értjük, amelyre a következők teljesülnek:

• |a×b|=|a|*|b|*sin(φ), ahol φ az a és b vektorok által bezárt szög;
• az a×b vektor merőleges mind az a, mind a b vektorra;
• az a, b és a×b vektorok ún. jobbrendszert alkotnak.

Az a, b és c vektorok jobbrendszert alkotnak, ha a c vektor irányából nézve az a vektort pozitív irányban el tudjuk forgatni a b vektorba az egyenesszögnél (arc 180°=π-nél) kisebb szöggel.
A jobbrendszert jobb kezünkkel is illusztrálhatjuk úgy, hogy
    – ha az a vektor irányába a hüvelykujjunkat és
    – a b vektor irányába a mutatóujjunkat állítjuk, akkor
    – a középső ujjunk éppen az a×b vektor irányába fog mutatni. (vö. Selényi-Szendrei 1969: 119-120).

A jobbrendszerhez hasonlóan a balrendszert a bal kezünk hüvelyk-, mutató- és középső ujjunkkal illusztrálhatjuk.

A fentiek alapján belátható (és kipróbálható), hogy ha az a, b és c vektorok (a,b,c) sorrendben jobbrendszert alkotnak, akkor

• (a,b,c) mellett (c,a,b) és (b,c,a) is jobbrendszert alkot,
• (a,b,−c) és (b,a,c) balrendszert alkot,
• (b,a,c) mellett (c,b,a) és (a,c,b) is balrendszert alkot.

Két vektor akkor és csak akkor párhuzamos egymással, ha vektoriális szorzatuk zérusvektor.

• Az a és b vektorok pontosan akkor párhuzamosak, ha van olyan λ∈ℝ valós szám, amelyre a=λ*b teljesül (vö. Juhász 2013: 65).

Adjuk meg az a=(a₁,a₂,a₃) és b=(b₁,b₂,b₃) térbeli vektorokat a térbeli Descartes-féle koordináta-rendszer az x, y és z tengelyeinek irányába mutató
    e_x=i, e_y=j, e_z=k
egységvektorokra mint bázisra vonatkozó koordinátáikkal. Ekkor az a és b vektorok vektoriális szorzata
    a×b= (a₂*b₃−a₃*b₂)*i − (a₁*b₃−a₃*b₁)*j + (a₁*b₂−a₂*b₁)*k
módon számítható ki.

A képletet legegyszerűbben a következő módon lehet megjegyezni:

a×b = det 

i	j	k
a1	a2	a3
b1	b2	b3

A fenti "determináns" formális kifejtése éppen a vektoriális szorzat kiszámítására vonatkozó képletet adja.

Legyenek a, b, és c tetszőleges térbeli vektorok, és λ tetszőleges valós szám (skalár). Ekkor a vektoriális szorzatra teljesülnek az alábbiak:

• a×b = −(b×a)
• λ*(a×b) = (λ*a)×b = a×(λ*b)
• a×(b+c) = (a×b)+(a×c)
• (a+b)×c = (a×c)+(b×c)

(2) Legyenek a, b, és c térbeli vektorok. Ekkor az (a×b)*c vektort az a, b, és c vektorok vegyes szorzatának nevezzük, és
    a·b·c=(a×b)*c
módon jelöljük.

Adjuk meg az a=(a₁,a₂,a₃), b=(b₁,b₂,b₃) és c=(c₁,c₂,c₃) térbeli vektorokat most is a térbeli Descartes-féle koordináta-rendszer az x, y és z tengelyeinek irányába mutató
    e_x=i, e_y=j, e_z=k
egységvektorokra mint bázisra vonatkozó koordinátáikkal. Ekkor az a, b és c vektorok vegyes szorzata a következő módon számítható ki:

a·b·c= = det 

a1	a2	a3
b1	b2	b3
c1	c2	c3

Három vektor akkor és csak akkor egysíkú (komplanáris) egymással, ha vegyes szorzatuk zérus.

---

Például tekintsük az alábbi vektorokat (vö. Selényi-Szendrei 1969: 133):
    a=(2,-3,1),
    b=(3,4,-2), és
    c=(0,3,6).

Ellenőrizzük az alábbi állításokat:

• a+b+c=(5,4,5)
• a−c=(2,-6,-5)
• (-5)*a=(-10,15,-5)
• a*b=-8
• b*c=0 (azaz b és c merőlegesek)
• |a|²=14
• |b|²=29
• a×c=(-21,-12,6)
• a·b·c=123
• (a×b)×c=(-9,-12,6)
• a×(b×c)=(-9,12,54)

8. Trigonometrikus függvények

A trigonometria "azokkal az összefüggésekkel foglalkozik, amelyek lehetővé teszik, hogy a háromszögek ismert alkatrészeiből az ismeretleneket számítással meghatározhassuk" (Obádovics 1972: 364).

Vizsgáljuk először a derékszögű háromszögeket a síkban. Legyen az A, B és C pontok által meghatározott ABC háromszög egy derékszögű háromszög, amelynek az AC és CB szakaszok a befogói (|AC|=b és |CB|=a), az AB szakasz pedig az átfogója (|AB|=c). Az AB átfogó és az AC befogó által bezárt hegyesszög legyen 'α' (a másik hegyesszög legyen β, a két befogó által bezárt szög pedig értelemszerűen derékszög).

Ha két derékszögű háromszög szögei megegyeznek, akkor a háromszögek hasonlóak, vagyis az egymásnak megfelelő oldalak aránya megegyezik. Ezért az oldalak aránya csak a szögek nagyságától függ. Ennek megfelelően az 'α' hegyesszögre értelmezhetjük az alábbi szögfüggvényeket:

• sin(α)=a/c^⇒
• cos(α)=b/c^⇒
• tg(α)=a/b=sin(α)/cos(α)
• ctg(α)=b/a=cos(α)/sin(α)

Tekintsünk egy tetszőleges ABC háromszöget (amelynek oldalai rendre a, b és c, szögei α, β és γ, területe pedig t). A háromszöget egy magasságvonal (pl. m_c) meghúzásával két derékszögű háromszögre bonthatunk. Alkalmazva a szögfüggvények meghatározását, valamint a Pitagorasz-tételt a derékszögű háromszögekre, az alábbi összefüggésekhez jutunk (vö. Obádovics 1972: 395-399):

• a/sin(α)=b/sin(β)=c/sin(γ) (szinusztétel)
• t=a*b*sin(γ)/2 (valamint t=b*c*sin(α)/2 és t=a*c*sin(β)/2)
• c²=a²+b²−2*a*b*cos(γ) (valamint a²=b²+c²−2*b*c*cos(α) és b²=a²+c²−2*a*c*cos(β)) (koszinusztétel)

A szinusz és koszinusz szögfüggvényekre érvényesek az alábbi összefüggések:

• Az ABC derékszögű háromszög másik hegyesszöge (β) esetén a szög melletti befogó 'a' és a szöggel szemközti befogó 'b', ezért
  sin(α)=a/c=cos(β)
  cos(α)=b/c=sin(β)
  teljesül.
• Mivel az ABC derékszögű háromszögben α+β=π/2 teljesül, ezért
  sin(α)=cos(β)=cos(π/2−α)
  cos(α)=sin(β)=sin(π/2−α)
  teljesül.
• Mivel az ABC derékszögű háromszögben a²+b²=c² teljesül (Pitagorasz-tétel), ezért
  sin²(α)+cos²(α)=1
  teljesül.

Az előző sin²(α)+cos²(α)=1 összefüggésből cos(α)=√1−sin²(α) következik, aminek segítségével például a tangensfüggvény kifejezhető a szinuszfüggvény segítségével
    tg(α)=sin(α)/√1−sin²(α)
módon. Ez az összefüggés közvetlenül is leolvasható egy olyan derékszögű háromszögből, amelynek az átfogóját 1-nek választjuk. Ekkor az α szöggel szemközti befogó hossza éppen sin(α) lesz, a másik befogó hossza pedig √1−sin²(α) lesz.

Néhány speciális szög esetén közvetlenül is meghatározhatjuk a szögfüggvények értékét:

α	sin(α)	cos(α)	tg(α)	ctg(α)
0	0	1	0	(nem értelmezett)
arc 30°=π/6	1/2	√3/2	√3/3	√3
arc 45°=π/4	√2/2	√2/2	1	1
arc 60°=π/3	√3/2	1/2	√3	√3/3
arc 90°=π/2	1	0	(nem értelmezett)	0

A fenti táblázatban szereplő értékek könnyen megkaphatóak, ha egy egységoldalú négyzetban vagy egy egységoldalú egyelő oldaló háromszögben vizsgáljuk egy átló, ill. magasságvonal által határolt derékszögű háromszögeket.

Ha az 'α' középponti szöghöz mint irányszöghöz tartozó szögszárat arc 90°=π/2 szöggel (pozitív irányban) elforgatjuk, akkor az α'=α+π/2 középponti szög szögfüggvényeire
    sin(α')=sin(α+π/2)=cos(α) és
    cos(α')=cos(α+π/2)=−sin(α)
teljesül.

Legyen az 'α' középponti szög egy hegyesszög, amelynek a mozgó szögszárát az egységkörön fekvő 'P' pontba mutató v egységvektor iránya jelöli ki. Forgassuk el a v vektort π/2-vel pozitív irányba, és az így kapott egységvektort jelöljük w-vel, a w vektor végpontját W-vel, irányszögét pedig α'=α+π/2-vel.

Mivel az OPV és OWQ háromszögek egybevágók,
    W(x,y)=(cos(α'),sin(α'))=(−sin(α),cos(α))
teljesül.

Ha a szinusz és koszinusz függvények értékét általánosítani akarjuk a [0,2*π) szögtartományra, akkor a korábbi definícióhoz^⇒ kell visszatérnünk:

Tegyük fel, hogy a derékszögű koordináta-rendszerben az 'α' forgásszöghöz mint középponti szöghöz tartozó ("mozgó") szögszár az egységsugarú kört a P(x,y) pontban metszi. Ekkor

• a P(x,y) pont első koordinátáját az 'α' szög koszinuszának nevezzük, azaz
  • cos(α) ⇋ x;
• a P(x,y) pont második koordinátáját az 'α' szög szinuszának nevezzük, azaz
  • sin(α) ⇋ y.

Az egységsugarú körön fekvő és az I. síknegyedben levő P(x,y) pontot
– először tükrözzük az 'y' tengelyre (P'),
– majd a P' pontot tükrözzük az 'x' tengelyre (P''),
– és végül a P'' pontot tükrözzük az 'y' tengelyre (P''').
Az alábbi ábráról olvassuk le a tükrözéssel kapott pontok koordinátáit, ha az I. síknegyedben levő P pont koordinátái 'x' és 'y':

• a II. síknegyedben P'(x,y)=(−x,y)
• a III. síknegyedben P''(x,y)=(−x,−y)
• a IV. síknegyedben P'''(x,y)=(x,−y)

Mivel az egységsugarú körön fekvő P(x,y) pont koordinátái éppen az α∈[0,π/2) hegyesszög mint középponti szög szögfüggvényei (azaz cos(α)=x és sin(α)=y teljesül), ezért a fenti összefüggéseket felhasználhatjuk a szögfüggvények értékének kiterjesztésére a II., III. és IV. síknegyedbe eső középponti szögek esetére:

I. síknegyed	II. síknegyed	III. síknegyed	IV. síknegyed
sin(α)	sin(π−α)=sin(α)	sin(π+α)=−sin(α)	sin(2*π−α)=−sin(α)
cos(α)	cos(π−α)=−cos(α)	cos(π+α)=−cos(α)	cos(2*π−α)=cos(α)
tg(α)	tg(π−α)=−tg(α)	tg(π+α)=tg(α)	tg(2*π−α)=−tg(α)
ctg(α)	ctg(π−α)=−ctg(α)	ctg(π+α)=ctg(α)	ctg(2*π−α)=−ctg(α)

Megjegyzés: a tangens és kotangens függvényekre vonatkozó összefüggések egyszerűen következnek a tg(α)=sin(α)/cos(α) és ctg(α)=cos(α)/sin(α) összefüggésekből. (Jegyezzük meg, hogy a fenti összefüggések tetszőleges 'α' szög esetén is érvényesek.)

A negatív (−α) középponti szöghöz (negatív irányszöghöz) tartozó Q(x,y) pont a pozitív 'α' középponti szöghöz (pozitív irányszöghöz) tartozó P(x,y) pontnak a koordinátarendszer 'x' tengelyére való tükrözésével kapható meg:

Az 'x' tengelyre való tükrözéssel kapott Q(x,y) pont koordinátái a 'P' pont 'x' és 'y' koordinátából
    Q(x,y)=(x,−y)
módon kaphatók meg. Ennek megfelelően egy negatív szög esetén az 'x' koordináta (azaz a koszinuszfüggvény értéke) nem változik, az 'y' koordináta (a szinuszfüggvény értéke) pedig előjelet vált. Vagyis teljesülnek az alábbi összefüggések:

• sin(−α)=−sin(α) (a szinuszfüggvény páratlan függvény);
• cos(−α)=cos(α) (a koszinuszfüggvény páros függvény);
• tg(−α)=−tg(α) (a tangensfüggvény páratlan függvény);
• ctg(−α)=−ctg(α) (a kotangensfüggvény páratlan függvény).

Mivel egy forgásszög 2*π nagyságú forgatás után önmagába megy át (és ugyanez történik akkor, ha k-szoros forgatást végzünk (ahol k∈ℤ tetszőleges egész szám), értelmezzük a szinusz- és koszinuszfüggvényt tetszőleges α+2*k*π szög esetén
sin(α+2*k*π) ⇋ sin(α)
cos(α+2*k*π) ⇋ cos(α)
módon, ahol 'α' a [0,2*π) szögtartományba eső tetszőleges szög. Ebből következik, hogy a szinusz- és koszinuszfüggvény 2*π-re periodikus függvény.

Mivel tg(α)=sin(α)/cos(α), ezért a tangensfüggvény (valamint a kotangensfüggvény) is 2*π-re periodikus függvény. Az egyes síknegyedekre vonatkozó táblázatból
    sin(α+π)/cos(α+π)=sin(α)/cos(α)
következik, továbbá a 2*π-re való periodicitásból a fenti összefüggés minden
    α+π+2*k*π=α+(2*k+1)*π
szögre is igaz (k∈ℤ). Ebből következik, hogy a tangensfüggvény értéke azonos lesz, ha a szöghöz π tetszőleges egész számszorosát (tetszőleges páros számszorosát vagy tetszőlegges páratlan számszorosát) hozzáadjuk. A tangensfüggvény (valamint a kotangensfüggvény) tehát π-re periodikus függvény.

Legyenek α és β tetszőleges szögek. Ezek szögfüggvényeire érvényesek az alábbi összefüggések (ún. addíciós tételek):

• sin(α+β)=sin(α)*cos(β)+cos(α)*sin(β)
• cos(α+β)=cos(α)*cos(β)−sin(α)*sin(β)
• sin(2*α)=2*sin(α)*cos(α)
• cos(2*α)=cos²(α)−sin²(α)

A szögfüggvényekre vonatkozó összefüggésekből további összefüggések vezethetőek le. Például sin(−β)=−sin(β) és cos(−β)=cos(β) miatt
    sin(α−β)=sin(α)*cos(β)−cos(α)*sin(β) és
    cos(α−β)=cos(α)*cos(β)+sin(α)*sin(β)
teljesül stb.

---

Oldjuk meg az alábbi feladatokat:

(1) Forgassuk el a síkban a derékszögű koordináta-rendszer természetes e_x, e_y bázisát α=π/6 szöggel.

Határozzuk meg

• a bázistranszformáció U mátrixát,^⇒
• az a=(4,2) és b=(1,3) vektorok nagyságát,
• a vektorok a*b skaláris szorzatának értékét a koordináták segítségével,
• a vektorok a*b skaláris szorzatának értékét az a*b=|a|*|b|*cos(γ) képlet segítségével (tipp: ha az a vektor irányszöge α, és a b vektor irányszöge β, akkor az a és b vektorok által bezárt γ szög γ=(β−α), amely a koszinuszfüggvényre vonatkozó addíciós tétel^⇒ segítségével meghatározható);
• az a=(4,2) és b=(1,3) vektorok koordinátáit az új bázisban,
• a vektorok a*b skaláris szorzatának értékét az új bázisban.

(2.1) Bizonyítsuk be a szinusztételt.

(2.2) Bizonyítsuk be az általános háromszög területének kiszámítására vonatkozó tételt.

(2.3) Bizonyítsuk be a koszinusztételt.

(3) Bizonyítsuk be, hogy egy AB szakaszt m:n arányban osztó 'P' pontba mutató p vektorra
p=(m*b+n*a)/(m+n)
teljesül, ahol a az 'A' pontba, b pedig a 'B' pontba mutató vektorok (vö. Selényi-Szendrei 1969: 103-104).

(4) Bizonyítsuk be, hogy egy háromszög súlyvonalai egy pontban, a súlypontban metszik egymást. A súlypontba mutató s vektor a háromszög csúcspontjaiba mutató a, b és c vektorok számtani közepe, azaz
    s=(a+b+c)/3
teljesül (vö. Selényi-Szendrei 1969: 115-116).

9.1 Koordinátarendszerek. Az egyenes és a sík egyenletei

Az analitikus geometria (másképpen koordináta-geometria) alapkérdése az, hogy "miként lehet egy pontsokaság minden pontját egyértelműen számadatokkal jellemezni. Ennek az a célja, hogy geometriai feladatokat [a] számítás módszerével oldjunk meg" (Selényi-Szendrei 1969: 157).

(1) A síkbeli vagy térbeli pontok helyzetét egy koordináta-rendszerhez viszonyítjuk. Adjuk meg a síkbeli Descartes-féle (vagy derékszögű) koordináta-rendszert két merőleges egységvektorral (e_x és e_y), a térbeli Descartes-féle koordináta-rendszert pedig három merőleges egységvektorral (e_x, e_y és e_z). Az egységvektorok definíció szerint jobbrendszert^⇒ alkotnak.

Az e_x, e_y és e_z vektorok kijelölik a koordináta-rendszer 'x', 'y' és 'z' tengelyeit. (A tengelyek az e_x, e_y és e_z vektorokkal párhuzamos számegyenesek, amelyek métszéspontja az origó.) Ennek megfelelően
– az 'x' tengely pontjait az x*e_x vektorok végpontjai,
– az 'y' tengely pontjait az y*e_y vektorok végpontjai, és
– a 'z' tengely pontjait a z*e_x vektorok végpontjai
adják meg, ahol x, y, z∈ℝ tetszőleges valós számok. (A síkban az 'x' tengelyt abszcissza-tengelynek, az 'y' tengelyt ordináta-tengelynek nevezzük. A térben két tetszőleges koordináta-tengely (az 'x' és 'y', az 'y' és 'z', valamint az 'x' és 'z' tengelyek) által meghatározott síkokat xy, yz és xz koordináta-síkoknak nevezzük.)

• Egy tetszőleges P(x,y) pont síkbeli koordinátáit úgy kapjuk meg, hogy a 'P' ponton keresztül párhuzamos egyeneseket húzunk a koordináta-tengelyekkel, és ahol ezek az egyenesek metszik a koordináta-tengelyeket, azok lesznek a 'P' pont síkbeli koordinátái.
• Egy tetszőleges P(x,y,z) pont térbeli koordinátáit úgy kapjuk meg, hogy a 'P' ponton keresztül párhuzamos síkokat húzunk a koordináta-síkokkal, és ahol ezek a síkok metszik a koordináta-tengelyeket, azok lesznek a 'P' pont térbeli koordinátái.

Ha a két dimenziós sík egy P(x,y) pontjába mutató vektor r, akkor a P(x,y) pont koordinátáit
    x=r*e_x=|r|*|e_x|*cos(α)=|r|*cos(α)
    y=r*e_y=|r|*|e_y|*cos(π/2−α)=|r|*sin(α)
adja meg, ahol 'α' az r vektor irányszöge. (Az 'x', ill. 'y' koordinátát a P(x,y) pont 'x', ill. 'y' tengelyre való merőleges vetülete adja meg.)

(a) Forgassuk el az r vektort pozitív írányba arc 90°=π/2 szöggel, és jelöljük az így kapott vektort r', végpontját pedig P'(x',y') módon. Mivel az elforgatott vektor hossza nem változik,
    x'=|r'|*cos(α')=|r|*cos(α+π/2)=−|r|*sin(α)^⇒ (x'=−y)
    y'=|r'|*sin(α')=|r|*sin(α+π/2)=|r|*cos(α)^⇒ (y'=x)
teljesül.

(b) Toljuk el az r vektort önmagával párhuzamosan úgy, hogy kezdőpontja egy adott d vektor D(d_x,d_y) végpontjával essen egybe. Jelöljük az így kapott vektort r', végpontját pedig P'(x',y') módon.

Az eltolással kapott vektor (r') a vektorok összefűzésének szabálya^⇒ szerint az eltolás vektorának (d) és az eltolt vektornak (r) az összege (azaz r'=d+r teljesül) ezért a koordinátákra
    x'=x+d_x
    y'=y+d_y
teljesül.

Tekintsük most a D(d_x,d_y)=O' pontot egy olyan koordináta-rendszer origójának, amelynek tengelyei párhuzamosak és egyirányúak az O koordináta-rendszer tengelyeivel. Mivel az OO' irányított szakasz megfelel az eltolás d vektorának, az O' koordináta-rendszert szemléletesen az O koordináta-rendszer "eltolásának" tekinthetjük.

Ebben az értelemben az O' koordináta-rendszerben ábrázolt r vektor megfelel az O koordináta-rendszerben ábrázolt r' vektornak.

Legyenek a három dimenziós térben a derékszögű koordináta-rendszer tengelyeit meghatározó egységvektorok e_x, e_y és e_z. Ekkor az a=(a₁,a₂,a₃) és b=(b₁,b₂,b₃) vektorok az egységvektorokkal
    a=a₁*e_x+a₂*e_y+a₃*e_z
és
    b=b₁*e_x+b₂*e_y+b₃*e_z
módon fejezhetőek ki. Mivel az egységvektorok páronként merőlegesek egymásra, ezért egyrészt
    a*b=a₁*b₁+a₂*b₂+a₃*b₃
teljesül, másrészt pedig például az a vektorra
    a*e_x=a₁
    a*e_y=a₂
    a*e_z=a₃
teljesül. Ha az a vektor x, y és z tengelyekkel bezárt szöge rendre α, β és γ, akkor az a vektor koordinátái
    a₁=|a|*cos(α)
    a₂=|a|*cos(β)
    a₃=|a|*cos(γ)
módon fejezhetőek ki. A cos(α), cos(β) és cos(γ) értékeket az a vektor iránykoszinuszainak nevezzük (ha az a vektor egységvektor, azaz |a|=1 teljesül, akkor koordinátái éppen megegyeznek az iránykoszinuszok értékével). Az iránykoszinuszokra teljesül a
    cos²(α)+cos²(β)+cos²(γ)=1
összefüggés.

A sikbeli, ill. térbeli koordináta-rendszerek segítségével a sík, ill. a tér minden pontjához pontosan egy valós számpár, ill. valós számhármas rendelhető hozzá.
Megfordítva: a koordináta-rendszerek segítségével minden valós számpárhoz, ill. valós számhármashoz pontosan egy síkbeli, ill. térbeli pont rendelhető hozzá.

Ha a síkban egy P(x,y) pontot a 'P' pontba mutató r vektor hosszával (vagyis az OP szakasz r=|r| hosszúságával), és a 'P' pontba mutató r vektor φ irányszögével (azaz az r vektor 'x' tengellyel bezárt szögével) adunk meg, ún. síkbeli polárkoordinátákról beszélünk. A Descartes-féle koordináta-rendszerben megadott koordináták és a polárkoordináták kapcsolata
    x=r*cos(φ)
    y=r*sin(φ)
illetve
    r=√x²+y²
    tg(φ)=y/x
módon adható meg.

(2) Adjunk meg egy egyenest a következő két vektorral:

• az egyenes egy adott P₀ pontjába mutató r₀ vektorral (a P₀ pont helyzetvektorával);
• az egyenessel párhuzamos v vektorral (az egyenes irányvektorával) (ahol v≠0, vagyis az irányvektor nem lehet zérusvektor).

Ekkor az egyenes egy tetszőleges 'P' pontjába mutató r helyzetvektort az
r=r₀+t*v
képlettel adhatjuk meg (ahol t∈ℝ egy valós szám). Ezt az egyenes paraméteres vektoregyenletének nevezzük. Ha r és r₀ az egyenes két különböző pontjába mutató vektor, akkor az r−r₀ vektor párhuzamos az egyenessel, tehát párhuzamos a v irányvektorral is. Ezért van olyan t∈ℝ valós szám, amelyre r−r₀=t*v teljesül.

Az egyenes r=r₀+t*v paraméteres vektoregyenlete meghatározza az egyenes pontjait a következő értelemben:

• az egyenes minden pontjához pontosan egy t∈ℝ valós szám tartozik;
• minden t∈ℝ valós szám meghatározza az egyenes pontosan egy pontját.

Ha a helyzetvektor térbeli koordinátái r₀=(x₀,y₀,z₀), az irányvektor koordinátái pedig v=(a,b,c), akkor az egyenes paraméteres vektoregyenlete felírható az alábbi egyenletrendszer segítségével:
    x=x₀+t*a
    y=y₀+t*b
    z=z₀+t*c
Ezt az egyenes paraméteres egyenletrendszerének nevezzük. Az egyenletrendszer (x,y,z) megoldásai a 't' paraméter különböző értékei mellett (t∈ℝ) az egyenes pontjait adják meg.

A síkban a fenti egyenletrendszer első két egyenlete adja meg az egyenes pontjait. Ha a v irányvektor egységvektor, amelynek irányszöge φ, akkor a fenti egyenletrendszer
    x=x₀+t*cos(φ)
    y=y₀+t*sin(φ)
alakban írható fel. (Mivel az egyenes pontjai nem függnek az irányvektor nagyságától, tetszőleges v irányvektor helyett használhatjuk a v^o=v/|v| egységvektort. Ezért a fenti egyenletrendszer bármilyen irányvektor esetén alkalmazható, ha irányszöge φ.)

Ha a síkbeli egyenes paraméteres egyenletrendszeréből kiküszöböljük a 't' paramétert, akkor az egyenes
y=m*(x−x₀)+y₀
egyenletét kapjuk, ahol m=sin(φ)/cos(φ) az egyenes iránytangense vagy meredeksége (az egyenes 'x' tengellyel bezárt φ irányszögének a tangense). Ha az egyenes adott P₀=(x₀,y₀) pontját úgy választjuk meg, hogy x₀=0 teljesüljön (azaz a P₀ pont az 'y' tengelyen legyen), akkor a fenti egyenlet az egyszerűbb
y=m*x+b
formában írható fel, ahol b=y₀ teljesül. (Mivel 'b' az egyenes és az 'y' tengely metszéspontjának 'y' koordinátája, "az az érték, ahol az egyenes az 'y' tengelyt metszi", 'b'-t az egyenes y-tengelymetszetének nevezzük.) Ez a síkbeli egyenes egyenletének iránytényezős alakja, "amelyben 'm' az egyenes iránytangense, 'b' pedig az y-tengelymetszet" (Selényi-Szendrei 1969: 174). Az egyenlet fontosabb speciális esetei:

• Ha az egyenes párhuzamos az 'x' tengellyel, akkor egyenlete y=b alakú ('x' értéke tetszőleges lehet).
• Ha az egyenes metszi a koordináta-rendszer origóját, akkor egyenlete y=m*x alakú.
• Ha az egyenes párhuzamos az 'y' tengellyel, akkor egyenlete x=a alakú, ahol 'a' tetszőleges valós szám ('y' értéke tetszőleges lehet).

Ha két egyenes iránytényezős alakban adott, és meredekségük m₁ és m₂ (feltéve, hogy egyikük sem párhuzamos az 'y' tengellyel), akkor

• az egyenesek párhuzamosak, ha meredekségük megegyezik, azaz m₁=m₂ teljesül;
• az egyenesek merőlegesek, ha m₁*m₂=−1, vagyis
      m₁=−1/m₂
  teljesül.

A merőlegességre vonatkozó szabály például a következőképpen látható be. A merőlegesség feltétele, hogy az irányvektorok skaláris szorzata zérus legyen. Legyenek az iránytényezős alakban megadott egyenesek egyenletei:
    y=m₁*x+b₁
    y=m₂*x+b₂
Ekkor az egyenesek két pontját könnyen megkaphatjuk például x=0 és x=1 mellett, ezekből pedig az egyenesek irányvektorai kifejezhetőek:
    v₁= (1,m₁+b₁)−(0,b₁)= (1,m₁)
    v₂= (1,m₂+b₂)−(0,b₂)= (1,m₂)
Az egyenesek merőlegesek, ha irányvektoraik skaláris szorzata zérus, azaz
    v₁*v₂= (1,m₁)*(1,m₂)= 1+m₁*m₂=0
Az utóbbi egyenletet átrendezve megkapjuk a merőlegesség
    m₁=−1/m₂
feltételét. (Megjegyzés: a fenti összefüggéshez az egyenesek
    n₁=(m₁,−1)
    n₂=(m₂,−1)
normálvektorainak skaláris szorzatát kiszámítva is eljuthatunk.)

Ha egy síkbeli egyenesnek adott két különböző, P₀=(x₀,y₀) és P₁=(x₁,y₁) pontja, amelyekre x₀≠x₁ teljesül (vagyis az egyenes nem párhuzamos az 'y' tengellyel), akkor az
    y₀=m*x₀+b
    y₁=m*x₁+b
egyenletrendszert 'm'-re és 'b'-re megoldva az egyenes 'm' meredeksége
    m=(y₁−y₀)/(x₁−x₀)
módon, az egyenes 'b' tengelymetszete pedig például
    b=y₀−m*x₀
módon számítható ki. Az y=m*x+b egyenletbe helyettesítve 'b'-t, kiemelve 'm'-et, majd behelyettesítve 'm'-et, az egyenes egyenlete
y=[(y₁−y₀)/(x₁−x₀)]*(x−x₀)+y₀
alakban írható fel. Ez a két adott ponton átmenő (síkbeli) egyenes egyenlete. (Az egyenlet helyessége könnyen ellenőrizhető x=x₀ és x=x₁ helyettesítéseket elvégezve.)

• Ha az egyenes két adott pontjára P₀=(a,0) (a≠0) és P₁=(0,b) teljesül (azaz P₀ az 'x' tengelyen, P₁ pedig az 'y' tengelyen helyezkedik el), akkor a fenti egyenlet
      y=(−b/a)*(x−a)
  alakú lesz.
  Ha az egyenes nem párhuzamos az 'x' tengellyel (azaz b≠0), akkor a fenti egyenlet
  x/a+y/b=1
  alakban írható fel (ahol 'a' az egyenes x-tengelymetszete, 'b' pedig az egyenes y-tengelymetszete). Ez az egyenlet a síkbeli egyenes tengelymetszetes alakja.

A síkbeli egyenes egyenlete mindig felírható
    A*x+B*y+C=0
alakban, ahol A, B és C tetszőleges valós számok, és az A és B számok egyszerre nem lehet zérusok.
    Megfordítva: minden olyan síkbeli pontsokaság, amelynek a P(x,y) pontjai leírhatók az
    A*x+B*y+C=0
egyenlettel, ahol A, B és C tetszőleges valós számok, és az A és B számok egyszerre nem lehetnek zérusok, egy síkbeli egyenest ad meg.

A fenti egyenlet a síkbeli egyenes egyenletének általános alakja.

Az egyenes paraméteres vektoregyenletéhez hasonlóan a síkot is leírhatjuk egy paraméteres vektoregyenlettel (és az ennek megfelelő egyenletrendszerrel). Adjunk meg egy síkot a következő vektorokkal:

• a sík egy adott P₀ pontjába mutató r₀ vektorral (a P₀ pont helyzetvektorával);
• a síkkal párhuzamos v₁ és v₂ vektorokkal (a sík két bázisvektorával), ahol
  • v₁≠0 és v₂≠0 (vagyis a vektorok nem zérusvektorok);
  • v₁∦v₂ (vagyis a vektorok nem párhuzamosak, azaz lineárisan függetlenek).

Ha r a sík egy tetszőleges P(x,y,z) pontjába mutató vektor, akkor az (r−r₀) vektor a síkban fekszik, vagyis kifejezhető a v₁ és v₂ bázisvektorok lineáris kombinációjaként. Tehát vannak olyan 't' és 'u' valós számok, amelyekre r−r₀=t*v₁+u*v₂ teljesül. Ezt átalakítva
r=r₀+t*v₁+u*v₂
adódik, ahol t, u∈ℝ tetszőleges valós számok. Ez a sík paraméteres vektoregyenlete.

(3) Adjunk meg egy egyenest a következő két vektorral:

• az egyenes egy adott P₀(x₀,y₀) pontjába mutató r₀ vektorral (a P₀ pont helyzetvektorával);
• az egyenesre merőleges n vektorral (az egyenes normálvektorával) (ahol n≠0, vagyis a normálvektor nem lehet zérusvektor).

Ekkor az egyenes egy tetszőleges P(x,y) pontjába mutató r helyzetvektort az
(r−r₀)*n=0
vektoregyenlettel adhatjuk meg. Ha r és r₀ az egyenes két különböző pontjába mutató vektor, akkor az (r−r₀) vektor párhuzamos az egyenessel, tehát merőleges az n normálvektorra (vagyis skaláris szorzatuk zérus).

Ha a helyzetvektor síkbeli koordinátái r₀=(x₀,y₀), a normálvektor koordinátái pedig n=(t,u), akkor az egyenes normálvektoros egyenlete felírható az alábbi egyenlet segítségével:
    (x−x₀)*t+(y−y₀)*u=0
Ha a normálvektor irányszöge α, hossza pedig |n|=n, akkor t=n*cos(α) és u=n*sin(α) miatt a fenti egyenlet
    (x−x₀)*cos(α)+(y−y₀)*sin(α)=0
alakban írható fel. Az egyenlet nem függ a normálvektor hosszától, és a normálvektor egyeneshez viszonyított irányától sem. (Ha az n normálvektor nem az egyenes irányába mutat, azaz α'=α+π irányszöggel rendelkezik, akkor cos(α')=−cos(α) és sin(α')=−sin(α) teljesül, mivel a szinuszfüggvény és koszinuszfüggvény harmadik síknegyedbeli előjele negatív. Ekkor (−1)-gyel beszorozva az egyenletet, mind α, mind α' irányszög esetén ugyanaz adódik.)
A fenti egyenletet átalakítva
    x*cos(α)+y*sin(α)= x₀*cos(α)+y₀*sin(α)= r₀*n^o
adódik.
Vezessük be a p=r₀*n^o jelölést az egyenlet jobb oldalán álló mennyiségre.
A p=r₀*n^o kifejezés az r₀ helyzetvektor merőleges vetületét adja meg az n^o egységvektorra, ezért csak az r₀ helyzetvektor x₀ és y₀ koordinátáitól, valamint az n normálvektor 'α' irányszögétől függ. A 'p' előjelét az n^o egységvektor iránya határozza meg: ha n^o az egyenes felé mutat, akkor p≥0, ellenkező esetben p≤0. De mivel korábban láttuk, hogy az egyenlet nem függ a normálvektor egyeneshez viszonyított irányától, elegendő azzal az esettel foglalkoznunk, amikor a normálvektor az egyenes irányába esik, azaz p=r₀*n^o≥0 teljesül.

Az alábbi ábrán az egyenes az 'y' tengelyt (0,b)-ben, az 'x' tengelyt pedig (a,0)-ban metszi.

Az egyenes |OB|=b y-tengelymetszetét a P₀(x₀,y₀) pont 'y' tengelyre vonatkozó merőleges vetületének M(0,y₀) metszéspontja két részre osztja, ezért
    b=y₀+m
ahol m=|MB| az MBP₀ derékszögű háromszög 'y' tengelyre eső befogója.
Emellett AOP∢=α és OBP∢ merőleges szárú szögek, ezért MBP₀∢=α, vagyis m/x₀=ctg(α), tehát
    m=x₀*ctg(α)
teljesül. Másrészt az OBP derékszögű háromszögben p=b*sin(α), tehát
    b=p/sin(α)
teljesül. A három egyenletből behelyettesítéssel
    p/sin(α)=y₀+x₀*ctg(α)
adódik, amiből ctg(α)=cos(α)/sin(α) miatt
    p=y₀*sin(α)+x₀*cos(α)
következik. Tehát a síkbeli egyenes normálvektoros egyenlete
x*cos(α)+y*sin(α)=p
alakban is írható, ahol 'α' az egyenes normálvektorának irányszöge, és 'p' az egyenes és a koordináta-rendszer origójának távolsága (p≥0). Ez a síkbeli egyenes egyenletének Hesse-féle normálalakja (vö. Obádovics 1972: 454-455).

Az alábbi ábrán négy egyenest ábrázolunk. Az egyenesek egyenletének x*cos(α)+y*sin(α)=p Hesse-féle normálalakjában az alábbi egyenesek (jobbról balra) a következő paramétereknek felelnek meg:

• 1. egyenes: p=100, α=π/6
• 2. egyenes: p=50, α=π/2+π/6
• 3. egyenes: p=50, α=π+π/6
• 4. egyenes: p=100, α=3*π/2+π/6

Adjunk meg egy síkot a következő két vektorral:

• a sík egy adott P₀ pontjába mutató r₀ vektorral (a P₀ pont helyzetvektorával);
• a síkra merőleges n vektorral (a sík normálvektorával) (ahol n≠0, vagyis a normálvektor nem lehet zérusvektor).

Ekkor a sík egy tetszőleges 'P' pontjába mutató r helyzetvektort az
(r−r₀)*n=0
vektoregyenlettel adhatjuk meg.

Adjunk meg egy síkot a sík három, nem egy egyenesbe eső P₀, P₁ és P₂ pontjába mutató r₀, r₁ és r₂ helyzetvektorokkal.

Ekkor a sík egy tetszőleges 'P' pontjába mutató r helyzetvektort az
(r−r₀)·(r₁−r₀)·(r₂−r₀)=0
vektoregyenlettel adhatjuk meg (ahol a '·' művelet a vektorok vegyes szorzatát^⇒ jelöli).

Végül tekintsük az
A*x+B*y+C*z+D=0
egyenletet, ahol A, B, C és D tetszőleges valós számok, és az A, B, C számok közül legalább az egyik zérustól különböző. Mivel
– a fenti egyenlet mindig egy síknak az egyenlete és
– egy adott sík egyenlete mindig a fenti alakra hozható,
ezért a fenti egyenlet a sík egyenletének általános alakját adja meg.

9.2. Feladatok

Számítsuk ki az ABC háromszög területét, ha a háromszög végpontjaira A(2,-1), B(1,4) és C(-3,2) teljesül. (Obádovics 1972: 452)

• adjuk meg a háromszög oldalainak megfelelő a=CA és b=BA vektorokat
• számítsuk ki a háromszög |a|=a és |b|=b oldalait
• számítsuk ki a az a*b skaláris szorzatot
• számítsuk ki a háromszög 'a' és 'b' oldala által bezárt γ szöget
• használjuk a t=a*b*sin(γ)/2 képletet

(megoldás: 11)

---

Határozzuk meg az A(2,−1) és B(3,4) pontokon átmenő egyenes egyenletét! (vö. Obádovics 1972: 457)

---

Számítsuk ki az 5*x−y+2=0 és 2*x−3*y+1=0 egyenesek metszéspontját és hajlásszögét! (vö. Obádovics 1972: 459)

(megoldás: a hajlásszög 45°)

---

Döntsük el, hogy a 4*x+3*y−15=0 és 3*x−4*y+15=0 egyenesek merőlegesek-e? (vö. Obádovics 1972: 459)

(megoldás: igen)

---

Döntsük el, hogy a 4*x−6*y+15=0, 5*x+4*y+13=0 és x+12*y−3=0 egyenesek egy pontban metszik-e egymást? (vö. Obádovics 1972: 461)

(megoldás: igen)

Határozzuk meg a P(5,3) pont távolságát a 3*x+4*y−7=0 egyenestől! (vö. Obádovics 1972: 463)

(megoldás: 4)

---

Adjunk konkrét értékeket az A, B, C paramétereknek, és határozzuk meg az A*x+B*y+C=0 egyenlettel adott e(x,y) egyenes alábbi jellemzőit az adott A, B és C esetén: (pl. A=1, B=−2, C=−4; A=3, B=−5, C=−10; stb.; érdemes a korábbi feladatokban szereplő egyenesekre elvégezni a feladatot) (vö. Obádovics 1972: 456)

• az e(x,y) egyenes tengelymetszetei, és az egyenes tengelymetszetes alakja
• az e(x,y) egyenes irányvektora, az irányvektor nagysága és irányszöge
• az e(x,y) egyenes paraméteres (irányvektoros) vektoregyenlete és paraméteres egyenletrendszere
• az e(x,y) egyenes meredeksége és egyenletének iránytényezős alakja
• az e(x,y) egyenes normálvektora, a normálvektor nagysága és irányszöge
• az e(x,y) egyenes egyenletének normálvektoros egyenlete és az egyenlet Hesse-féle normálalakja

---

Adjunk konkrét értékeket az A, B, C, u, v és α paramétereknek, és határozzuk meg az A*x+B*y+C=0 egyenlettel adott e(x,y) egyenes, P(u,v) pont és 'α' szög esetén az alábbi jellemzőket:

• a P(u,v) ponton áthaladó és az e(x,y) egyenessel párhuzamos egyenes
• a P(u,v) ponton áthaladó és az e(x,y) egyenesre merőleges egyenes
• a P(u,v) ponton áthaladó és az e(x,y) egyenessel 'α' szöget bezáró egyenes

10.1 A kör és a parabola egyenlete

(1) A kör a sík azon pontjainak mértani helye, amelyek egy adott ponttól, a kör középpontjától egyenlő távolságra vannak (vö. Obádovics 1972: 468).

Adjunk meg egy kört a következő módon:

• a kör K₀(a,b) középpontjába mutató r₀ vektorral (a K₀ középpont helyzetvektorával);
• a kör r sugarával.

Ekkor a kör egy tetszőleges P(x,y) pontjába mutató r helyzetvektort az     |r−r₀|=r
képlettel, vagy ezt négyzetre emelve az
(r−r₀)²=r²
képlettel adhatjuk meg (ahol egy vektor négyzete alatt hosszúsága négyzetét értjük, amit az önmagával vett skaláris szorzattal számíthatunk ki). Ezt koordinátákkal kifejezve az
(x−a)²+(y−b)²=r²
egyenlethez jutunk. Ezt a kör általános egyenletének nevezzük. Ha r a kör egy tetszőleges pontjába mutató vektor és r₀ a kör középpontjába mutató vektor, akkor az (r−r₀) vektor nagysága éppen a kör sugarát adja meg.

Ha a kör középpontja a koordináta-rendszer origójával esik egybe, akkor a=0 és b=0 miatt a kör középponti egyenletét kapjuk:
    x²+y²=r²

Ha az origó középpontú kör egy P(x,y) pontjába mutató r helyzetvektort polárkoordinátákkal (azaz a vektor 'r' hosszával és t=α irányszögével) adjuk meg, akkor a kör paraméteres egyenletrendszerét kapjuk:
    x=r*cos(t)
    y=r*sin(t)
ahol a 't' paraméterre t∈[0,2*π) teljesül. "Ha 't' befutja a 0≤t<2*π intervallumot, r végpontja leírja a kört." (Reiman 1992: 345)

Húzzuk meg a kör egy P₀(x₀,y₀) pontjában a kör érintőjét.

Az érintő P₀ pontjába mutató helyzetvektor r, a kör K₀(a,b) középpontjából a P₀(x₀,y₀) pontba mutató (r−r₀) vektor pedig merőleges az egyenesre, ezért az egyenes egy normálvektorát adja.

Ezért az egyenes egy tetszőleges Q(x,y) pontjába mutató q vektorral felírhatjuk az egyenes normálvektoros egyenletét:
    (q−r)*(r−r₀)=0

Az érintő normálvektoros egyenletét koordinátákkal felírva az
    (x−x₀)*(x₀−a)+(y−y₀)*(y₀−b)=0
egyenletet kapjuk (ahol K₀(a,b) a kör középpontja, P₀(x₀,y₀) pedig az egyenes és a kör érintkezési pontja).

---

Feladat: határozzuk meg annak a feltételét, hogy egy origó középpontú, 'r' sugarú körnek és egy iránytényezős alakban megadott ('m' meredekségű és 'b' tengelymetszetű) egyenesnek

• két közös pontja legyen (az egyenes metszi a kört);
• egy közös pontja legyen (az egyenes érinti a kört);
• ne legyen közös pontja.

---

(2) A parabola azoknak a pontoknak a halmaza a síkon, amelyek a sík egy 'F' pontjától és egy, az 'F' pontot nem tartalmazó 'd' egyenesétől egyenlő 'p' távolságra vannak. (vö. Rieman 1992: 349)

• Az 'F' pontot a parabola fókuszának (fókuszpontjának, gyújtópontjának) nevezzük.
• A 'd' egyenest a parabola vezéregyenesének (direktrixének) nevezzük.
• Az 'F' ponton átmenő ás a 'd' egyenesre merőleges 't' egyenes a parabola tengelye vagy szimmetriatengelye. (A parabola szimmetrikus a 't' tengelyre.)
• A parabola és a szimmetriatengely metszéspontja a 'C' tengelypont vagy csúcspont. (A tengelypont a 'd' vezéregyenestől és az 'F' fókuszponttól azonos 'p' távolságra van.)

Vizsgáljunk egy olyan parabolát, amelyre a következők teljesülnek:
– a 'd' vezéregyenes párhuzamos a koordináta-rendszer 'x' tengelyével, az 'x' tengely alatt helyezkedik el, és távolsága az 'x' tengelytől 'p' (tehát egyenlete y=−p);
– a 't' szimmetriatengely egybeesik a koordináta-rendszer 'y' tengelyével;
– a tengelypont koordinátái C(0,0), azaz a tengelypont egybeesik a koordináta-rendszer origójával;
– a fókuszpont koordinátái F(0,p).

A szakirodalomban számos helyen (pl. Obádovics 1972; Rieman 1992; Selényi-Szendrei 1969) a fókuszponttól és a vezéregyenestől mért távolságot (p) a p'=2*p paraméterrel jelölik. Ebben az esetben például a fókuszpont és a tengelypont, valamint a tengelypont és a vezéregyenes távosága p'/2=p, a fókuszpont és a vezéregyenes távosága p'=2*p stb., és p↔p'/2 helyettesítést kell végrehajtanunk az egyenletekben.

Az ilyen elhelyezkedésű parabolát normálparabolának ("felülről nyitott" parabolának) nevezzük.

Ekkor a parabola egy tetszőleges P(x,y) pontjának távolsága az F(0,p) fókuszponttól 'p', azaz
    x²+(y−p)²=p²
teljesül. Emellett a P(x,y) pont merőleges vetülete a 'd' egyenesre a Q(x,-p) pont, és mivel a P(x,y) pont és a Q(x,-p) távolsága szintén 'p', ezért
    (y+p)²=p²
teljesül. A két egyenletből
    x²+(y−p)²=(y+p)²
következik, amit egyszerűsítve kapjuk a normálparabola egyenletét:
y=x²/(4*p)

Ha a normálparabolát 90° fokkal jobbra vagy balra elforgatjuk, a következő parabolákhoz jutunk:

A "jobbról nyitott" parabola esetében a koordináta-rendszer 'x' és 'y' tengelye "éppen szerepet cserél" (vö. Rieman 1992: 351). A 90° fokkal jobbra elforgatott parabola esetén a parabola egy tetszőleges P(x,y) pontja a P'(x',y') pontba megy át, ahol
    x'=y
    y'=−x
teljesül. Ebből
    x'=(−y')²/(4*p)
adódik, tehát a "jobbra nyitott" parabola egyenlete
y'=±√4*p*x' vagy y'²=4*p*x'
alakú lesz (ahol x'∈[0,+∞) teljesül).

Ha a normálparabolát egy e(u,v) vektorral eltoljuk, akkor a parabola egy tetszőleges P(x,y) pontja a P'(x',y') pontba megy át, ahol
    x'=x+u
    y'=y+v
teljesül. Ebből
    (y'−v)=(x'−u)²/(4*p)
adódik, tehát az e(u,v) vektorral eltolt normálparabola egyenlete
y'=(x'−u)²/(4*p)+v
alakú lesz. Az így eltolt parabola tengelypontja C'(u,v) lesz.

Minden olyan síkbeli parabola egyenlete, amelynek a szimmetriatengelye párhuzamos a koordináta-rendszer 'y' tengelyével,
    y=a*x²+b*x+c
alakú, ahol a, b, c∈ℝ tetszőleges számok, és a≠0 teljesül.
Megfordítva: minden olyan síkbeli pontsokaság, amelynek az egyenlete
    y=a*x²+b*x+c
alakú, ahol a, b, c∈ℝ tetszőleges számok, és a≠0 teljesül, egy 'y' tengellyel párhuzamos szimmetriatengelyű parabola egyenlete.

Ha a>0 teljesül, a parabola "felfelé nyitott"; ha pedig a<0 teljesül, akkor a parabola "lefelé nyitott".

---

---

---

(→ előző témakörök)

---

Boda István, 2021.