A továbbiakban legyen f : A⊆ℝ → B⊆ℝ a valós számokon értelmezett (ún. egyváltozós) függvény, amelynek értelmezési tartománya
és értékkészlete
a valós számok egy részhalmaza.
A függvényt rendszerint egy síkbeli, derékszögű (Descartes-féle)
koordináta-rendszerben
ábrázoljuk, ahol
– az 'x' tengely (az abszcissza) pontjainak az értelmezési tartomány lehetséges elemei,
– az 'y' tengely (az ordináta) pontjainak az értékkészlet lehetséges elemei,
– a függvény grafikonjának pedig a sík azon (x,y) pontjai felelnek meg, amelyekre y=f(x).
(Jegyezzük meg, hogy a függvény definíciója alapján az x∈A független változó bármely értékéhez pontosan egy y∈B függvényérték tartozik.)
A Descartes-féle koordináta-rendszerben két pont,
P1(x1,y1) és
P2(x2,y2)
távolsága
P1P2 =
√((x1−x2)2+(y1−y2)2)
módon adható meg.
Értelmezzük az f(x)=∣x∣ : ℝ → ℝ abszolút érték függvényt a következőképpen:
| ∣x∣ = | { | x ha x≥0 |
| −x ha x<0 |
A függvény görbéje:
Az abszolút értékre vonatkozó néhány fontosabb összefüggés (vö. Farkas 2001: 38-39):
Legyenek x,y∈ℝ tetszőleges valós számok, ekkor
|x|≥0
|x*y|=|x|*|y|
|x+y|≤|x|+|y|, ill. általánosan
|x1+x2+...+xn|≤|x1|+|x2|+...+|xn| (xi∈ℝ, 1≤i≤n, n∈ℕ)
Az ún. háromszög-egyenlőtlenség általánosításának egy lehetséges bizonyítása:
(x+y)2=
x2+2*x*y+y2≤
x2+2*|x|*|y|+y2=
(|x|+|y|)2
vagyis
0≤(x+y)2≤(|x|+|y|)2
teljesül.
Mivel a négyzetgyökfüggvény nemnegatív számok esetén szigorúan monoton növekvő, a fenti egyenlőtlenségből
|x+y|≤|x|+|y|
következik.
|x−y|=|y−x|
|x−y|≤|x|+|y| vagy |y−x|≤|x|+|y|
||x|−|y||≤|x+y| vagy ||y|−|x||≤|x+y|
||x|−|y||≤|x−y| vagy ||x|−|y||≤|y−x|
Legyenek x1, x2, ..., xn és y1, y2, ..., yn tetszőleges valós számok (n∈ℕ). Ekkor
|x1*y1+x2*y2+...+xn*yn| ≤
(√x12+x22+...+xn2)*(√y12+y22+...+yn2) vagy másképpen felírva
|x1*y1+x2*y2+...+xn*yn| ≤
√(x12+x22+...+xn2)*(y12+y22+...+yn2)
teljesül. (ún. Cauchy-Bunyakovszkij-Schwarz egyenlőtlenség vagy CBS egyenlőtlenség).
Értelmezzük az f(x)=sgn(x) : ℝ → ℝ előjel függvényt a következőképpen:
| sgn(x) = | { | 1 ha x>0 |
| 0 ha x=0 | ||
| −1 ha x<0 |
A függvény görbéje:
Értelmezzük az f(x)=[x] : ℝ → ℝ (alsó) egészrész függvényt a következőképpen:
[x] = max {n∈ℤ | n≤x}
Érdemes megjegyezni, hogy az egészrész függvény csak nemnegatív számokra egyezik meg a törtrész (ti. a tizedesjegyek) levágásával kapott egész számmal (pl. [0.97]=0, [3.14]=3), negatív számokra a törtrész levágása után kapott számnál eggyel kisebb (negatív) számot kapunk (pl. [-1.23]=-2, [-8.67]=-9).
Írjon be egy számot:
A függvény értéke:
Az egészrész függvény görbéje:
Értelmezzük az f(x)={x} : ℝ → ℝ törtrész függvényt a következőképpen:
{x} = x − max {n∈ℤ | n≤x} = x − [x]
Mivel egy szám egészrésze mindig kisebb vagy egyenlő, mint maga a szám ([x]≤x<[x]+1), a törtrész függvény értéke 0≤{x}<1 közötti nemnegatív valós szám.
Érdemes megjegyezni, hogy a törtrész függvény csak nemnegatív számokra egyezik meg az egész rész levágásával kapott tizedestörttel (pl. [0.97]=0.97, [3.14]=0.14), negatív számokra a törtrész függvény értéke a levágott (nemnegatív) tizedestörtet +1-re egészíti ki (pl. [-1.23]=0.77, [-8.67]=0.33).
Írjon be egy számot:
A függvény értéke:
(8 tizedesjegy pontossággal)
A törtrész függvény görbéje:
Értelmezzük az f(x) : ℝ → ℝ lineáris függvényt a következőképpen:
f(x) = m*x + c (m,c ∈ ℝ)
Ha m=0, akkor az f(x)=c függvényt konstans függvénynek nevezzük.
Ha c=0, akkor az y=m*x függvényt egyenes arányosságnak nevezzük. Például ha egy gépkocsi állandó sebességgel halad, akkor s=f(t)=v*t, vagyis ha 'v' állandó, akkor a gépkocsi által megtett 's' út és az ennek megtételéhez szükséges 't' idő egymással egyenesen arányos.
Ha m≠0 teljesül, a lineáris függvény zérushelye −c/m.
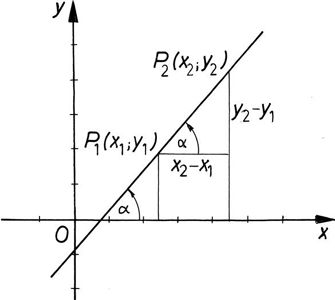
Az 'm' értéke a lineáris függvény meredeksége (a függvény grafikonjának a koordináta rendszer 'x' tengelyével bezárt szögének tangense), azaz a függvény két tetszőleges pontjában
m=tg(α)=(y2−y1)/(x2−x1)=(f(x2)−f(x1))/(x2−x1)
(ld. az ábrát):

Ha az f(x) lineáris függvény meredeksége (m) ismert, és adott a görbe egy (x0,f(x0)) pontja, akkor a lineáris függvény f(x)=m*(x−x0)+f(x0) formában írható fel.
Például az f(x) = 2*x−40 és a g(x) = −3*x+60 függvény görbéi:
Két lineáris függvényből és az egészrész függvényből egy "cikcakkos" függvényt is felépíthetünk:
| f(x) = | { | 3*x−[x]/2 | ha [x] páros |
| 2*x+([x]+1)/2 | ha [x] páratlan |
Egy 'n' segédváltozóval ez a függvény a következőképpen írható fel:
| f(x) = | { | 3*x−n | ha x∈[2*n,2*n+1) (n∈ℤ) ([x]=2*n) |
| 2*x+(n+1) | ha x∈[2*n+1,2*(n+1)) (n∈ℤ) ([x]=2*n+1) |
A függvény folytonos és invertálható; inverze:
| f−1(y) = | { | (y+n)/3 | ha x∈[2*n,2*n+1) (n∈ℤ) |
| (y−(n+1))/2 | ha x∈[2*n+1,2*(n+1)) (n∈ℤ) |
Mivel x=f−1(y), ezért x∈[2*n,2*n+1) és x∈[2*n+1,2*(n+1)) felírható a következő módon:
2*n≤(y+n)/3≤2*n+1
és
2*n+1≤(y−(n+1))/2≤2*(n+1)
A fenti egyenlőtlenségeket megoldva y-ra a következő függvényt kapjuk:
| f−1(y) = | { | (y+n)/3 | ha y∈[5*n,5*n+3) (n∈ℤ) ([y]=5*n vagy [y]=5*n+1 vagy [y]=5*n+2) |
| (y−(n+1))/2 | ha y∈[5*n+3,5*(n+1)) (n∈ℤ) ([y]=5*n+3 vagy [y]=5*n+4) |
Az inverz függvény képletében n-t [y]-nal kifejezve és a kapott kifejezéseket átalakítva a következő függvényt kapjuk:
| f−1(y) = | { | y/3+[y]/15 | ha [y] osztható 5-tel, azaz [y]≡0 (mod 5) |
| y/3+([y]−1)/15 | ha [y]≡1 (mod 5) | ||
| y/3+([y]−2)/15 | ha [y]≡2 (mod 5) | ||
| y/2−([y]+2)/10 | ha [y]≡3 (mod 5) | ||
| y/2−([y]+1)/10 | ha [y]≡4 (mod 5) |
A függvények görbéi:
Értelmezzük az f(x) : ℝ → ℝ függvényt a következőképpen:
f(x) = xn (n∈ℕ)
Az f(x) = x2 függvény görbéje:
Az f(x) = x3 függvény görbéje:
Az f(x)=x4, f(x)=x5 és f(x)=x6 függvény görbéi:
A hatványozással kapcsolatos néhány fontosabb azonosság (x,y∈ℝ, n,m∈ℕ):
xn * yn = (x*y)n
xn * xm = xn+m
(xn)m = xn*m
x2−y2 = (x+y)*(x−y)
x3−y3 = (x2+x*y+y2)*(x−y)
...
xn−yn =
(xn−1+xn−2*y+xn−3*y2+...+x*yn−2+yn−1)*(x−y)
Például ha x=q, y=1, akkor a fenti képlet a qn−1 = (qn−1+qn−2+qn−3+...+q+1)*(q−1) összefüggést adja, ami lehetővé teszi, hogy egyszerűen kiszámítsuk a mértani sorozat első 'n' tagjának összegét.
x2−y2 = (x−y)*(x+y)
x3+y3 = (x2−x*y+y2)*(x+y)
x4−y4 = (x3−x2*y+x*y2−y3)*(x+y)
x5+y5 = (x4−x3*y+x2*y2−x*y3+y4)*(x+y)
...
A binomiális tétel:
| ( | n | ) | ( | n | ) | ( | n | ) | ( | n | ) | ( | n | ) | ||||||
| (x+y)n = | xn + | xn−1*y + | xn−2*y2 +...+ | x*yn−1 + | yn | |||||||||||||||
| 0 | 1 | 2 | n−1 | n | ||||||||||||||||
ahol az xn−k*yk tényezők együtthatója az ún. binomiális együttható:
A binomiális tétel x=1 és y=1 esetre alkalmazva:
| ( | n | ) | ( | n | ) | ( | n | ) | ( | n | ) | ( | n | ) | ||||||
| 2n = | + | + | +...+ | + | ||||||||||||||||
| 0 | 1 | 2 | n−1 | n | ||||||||||||||||
Legyen r∈ℝ valós szám, amelyre r>−1 és r≠0, valamint n∈ℕ természetes szám, amelyre n≥2 teljesül; ekkor
(1 + r)n > 1 + n*r
teljesül (ún. Bernoulli-egyenlőtlenség; vö. Farkas 2001: 37-38).
Értelmezzük az f(x) : ℝ → ℝ n-ed fokú racionális egészfüggvényt a következőképpen:
f(x) = an*xn + an−1*xn−1 + ... + a2*x2 + a1*x1 + a0 (ai ∈ ℝ, i=0,1,...,n; an≠0)
A komplex számok körében a racionális egészfüggvény gyöktényezős alakja
f(x) = an*(x−x1)r1
*(x−x2)r2
*...
*(x−xs)rs
ahol az x1, x2, ..., xs valós számok az f(x) polinom r1, r2, ..., rs-szeres gyökei (zérushelyei). Az algebra alaptétele alapján a komplex számok körében
r1 + r2 + ... + rs = n
teljesül (a valós számok körében általános esetben a polinomok első és másodfokú tényezők szorzataként írhatóak fel).
Az f(x)=x2+14*x−120=(x+20)*(x−6), g(x)=−x2+28*x−196=−(x−14)2 és h(x)=x2−3*x+20 másodfokú függvények görbéi:
Az y = x3−36*x2−36*x+1296 = (x+6)*(x−6)*(x−36) harmadfokú függvény görbéje:
A matematikában a polinomok nagyon fontos szerepet játszanak.
Értelmezzük az f(x) : ℝ∖{0} → ℝ függvényt a következőképpen:
f(x) = 1/x (x∈ℝ, x≠0) ≔ x−1
A függvény görbéje:
Ha a∈ℝ tetszőleges valós szám, az f(x) = a/x (x∈ℝ, x≠0) függvényt fordított arányosságnak nevezzük. Például ha egy gépkocsi egy meghatározott 's' távolságot egyenletes sebességgel tesz meg, akkor az s=v*t összefüggés miatt t=f(v)=s/v, vagyis ha 's' állandó, akkor a gépkocsi 'v' sebessége és a távolság megtételéhez szükséges 't' idő egymással fordítottan arányos.
A függvény görbéje pl. a=2, a=−3 és a=4 mellett:
Értelmezzük az f(x) : ℝ∖{0} → ℝ függvényt a következőképpen:
f(x) = 1/xn (x∈ℝ, x≠0) ≔ x−n (n∈ℕ)
A függvény görbéje n=2 esetén:
Értelmezzük az f(x) : ℝ+∪{0} → ℝ függvényt a következőképpen:
f(x) = √x (x∈ℝ, x≥0) ≔ x1/2
A négyzetgyökfüggvény görbéje:
A ±√x függvények görbéi egy grafikonon ábrázolva:
Értelmezzük az f(x) : ℝ → ℝ köbgyökfüggvényt a következőképpen:
f(x) = 3√x ≔ x1/3
A köbgyökfüggvény görbéje:
Értelmezzük az f(x)=sin(x) : ℝ → [−1;1] ⊆ ℝ trigonometrikus függvényt a következőképpen:
– ha x=0, akkor legyen sin(x) = 0
– ha 0<x<π/2, akkor legyen sin(x) = {egy 'x' hegyesszögű derékszögű háromszög szöggel szemközti befogójának és átfogójának a hányadosa}
– ha x=π/2, akkor legyen sin(x) = 1
– ha π/2<x<π, akkor legyen sin(x) = sin(π−x)
– ha x=π akkor legyen sin(x) = 0
– ha π<x<3*π/2, akkor legyen sin(x) = −sin(x−π)
– ha x=3*π/2 akkor legyen sin(x) = −1
– ha 3*π/2<x<2*π, akkor legyen sin(x) = −sin(2*π−x)
Ha x<0 vagy x≥2*π, akkor legyen sin(x) = sin(x + 2*π).
A függvény görbéje:
Értelmezzük az f(x)=cos(x) : ℝ → [−1;1] ⊆ ℝ trigonometrikus függvényt a következőképpen:
– ha x=0, akkor legyen cos(x) = 1
– ha 0<x<π/2, akkor legyen cos(x) = {egy 'x' hegyesszögű derékszögű háromszög szög melletti befogójának és átfogójának a hányadosa}
– ha x=π/2, akkor legyen cos(x) = 0
– ha π/2<x<π, akkor legyen cos(x) = −cos(π−x)
– ha x=π akkor legyen cos(x) = −1
– ha π<x<3*π/2, akkor legyen cos(x) = −cos(x−π)
– ha x=3*π/2 akkor legyen cos(x) = 0
– ha 3*π/2<x<2*π, akkor legyen cos(x) = cos(2*π−x)
Ha x<0 vagy x≥2*π, akkor legyen cos(x) = cos(x + 2*π).
A függvény görbéje:
A szinusz- és koszinuszfüggvényre vonatkozó fontosabb azonosságok:
α[radián] = i/r (egy 'r' sugarú körben az α belső szög nagysága radiánban vagy ívmértékben kifejezve megegyezik a szöghöz tartozó körív és a kör sugarának hányadosával)
Például:
360[fok] = 2*π[radián];
180[fok] = π[radián];
90[fok] = π/2[radián];
60[fok] = π/3[radián];
45[fok] = π/4[radián];
30[fok] = π/6[radián];
stb.
Általánosan:
α[fok] = α[radián]*180/π
α[radián] = α[fok]*π/180
sin(−x) = −sin(x)
cos(−x) = cos(x)
cos(x) = sin(π/2 − x)
sin(x) = cos(π/2 − x)
sin2(x) + cos2(x) = 1
sin(x + y) = sin(x)*cos(y) + cos(x)*sin(y)
cos(x + y) = cos(x)*cos(y) − sin(x)*sin(y)
sin(2*x) = 2*sin(x)*cos(x)
cos(2*x) = cos2(x) − sin2(x)
sin(π/6) = cos(π/3) = 1/2 és
sin(π/3) = cos(π/6) = √3/2 (tipp: vegyünk fel egy egységoldalú egyenlő oldalú háromszöget, amelyben egy magasság két 30°/60°-os derékszögű háromszöget jelöl ki)
sin(π/4) = cos(π/4) = 1/√2 (tipp: vegyünk fel egy egységoldalú négyzetet, amelyben egy átló két egyenlő szárú, 45°-os derékszögű háromszöget jelöl ki)
Értelmezzük az f(x) : ℝ∖{k*π | k∈ℤ} → ℝ függvényt a következőképpen:
f(x) = 1/sin(x) (x≠k*π, k∈ℤ)
A függvény görbéje:
Értelmezzük az f(x) : ℝ → ℝ függvényt a következőképpen:
| f(x) = | { | sin(x)/x | ha x≠0 |
| 1 | ha x=0 |
Írjon be egy számot:
A függvény értéke:
A függvény görbéje:
Értelmezzük az f(x) : ℝ∖{0} → ℝ függvényt a következőképpen:
f(x) = sin(1/x) (x≠0)
A függvény görbéje:
Értelmezzük az f(x)=tg(x) : A⊆ℝ → ℝ trigonometrikus függvényt a következőképpen:
tg(x) = sin(x) / cos(x) {x≠π/2+k*π, k∈ℤ}
Az f(x)=tg(x) függvény az egységsugarú körben közvetlenül is értelmezhető:
A tangensfüggvény görbéje:
Értelmezzük az f(x)=ax : ℝ → ℝ+ (a∈ℝ, a>0, a≠1) exponenciális függvényt a következőképpen:
(0) ha x=0, akkor legyen ax = a0 = 1;
(1) ha n∈ℕ tetszőleges természetes szám, akkor legyen
a−n = 1/an;
(2) ha x=p/q∈ℚ tetszőleges racionális szám (p,q∈ℤ, q>0), akkor legyen
ax = (q√ap) (jegyezzük meg, hogy a>0);
(3) ha x∈ℝ tetszőleges valós szám, akkor legyen
ℚx−0 = ℚ ∩ (−∞,u) az 'x'-nél kisebb és
ℚ'x+0 = ℚ ∩ (v,+∞) az 'x'-nél nagyobb racionális számok halmaza;
ekkor legyen ax = h∈ℝ+ az a (pozitív) valós szám, amelyre
∀(u∈ℚx−0)
∀(v∈ℚ'x+0)
(au < h < av)
teljesül.
Az f(x)=ex : ℝ → ℝ+ függvényt, ahol
e≈2,718281828
az ún. Euler-féle szám
(a természetes logaritmus alapszáma),
szűkebb értelemben vett (e alapú) exponenciális függvénynek nevezzük.
Az f(x)=ex és g(x)=e−x függvény görbéje:
Az exponenciális függvényre vonatkozó fontosabb azonosságok:
a0 = 1
ax * bx = (a*b)x
ax * ay = ax+y
(ax)n = an*x (n∈ℕ)
Az Euler-féle e számot például a következő konvergens számsorozattal állíthatjuk elő:
sn = (1 + 1/n)n
A sorozat határértéke:
lim sn = e ≈ 2,718281828
n→∞
A sorozat első 10+5 eleme:
| n | sn=(1+1/n)n | Δ=e−sn |
|---|---|---|
| ... | ... | |
| ... | ... | |
| ... | ... | |
| ... | ... | |
| ... | ... |
A sorozat határértékének létezéséhez elegendő a sorozat monotonitását és korlátosságát bizonyítani. Előbbihez például a binomiális tételt, utóbbihoz pedig a mértani sorozat összegképletét használhatjuk fel (vö. Farkas 2001: 61-62).
Az f(x)=(1 + 1/x)x függvény végtelenben vett határértéke szintén az Euler-féle e számot állítja elő:
lim f(x) = e
x→∞
Az f(x)=(1 + x/n)n sorozat végtelenben vett határértéke az ex exponenciális függvényt állítja elő:
lim f(x) = ex
n→∞
Az alábbi sorozat elemei közelítőleg n! értékét adják meg (ún. Stirling-formula):
sn = √2*π*n*(n/e)n
A sorozat első 15 eleme:
| n | sn=√2*π*n*(n/e)n | n! | Δ=(n!−sn)/n![%] |
|---|
Az
f(x)=e−x2 : ℝ → ℝ+
függvényt, vagy egyszerűbben írva az
f(x)=exp(−x2)
függvényt haranggörbének nevezzük. A normális eloszlás görbéjét ebből a függvényből képezzük
![[a Gauss-eloszlásfüggvény képlete]](kepek/gauss_fv.gif) (m,σ∈ℝ, σ>0)
(m,σ∈ℝ, σ>0)
módon (az 'm' paraméter a normális eloszlás
várható értéke
és a 'σ' paraméter a normális eloszlás
szórása).
Ha m=0 és σ=1, akkor ún. standard normális eloszlásról szokás beszélni.
Az f(x)=exp(−x2), g(x)=2*exp(−(2*x)2) h(x)=1.5*exp(−(x/2)2) függvények görbéi:
Értelmezzük az f(x)=loga(x) : ℝ+ → ℝ (a∈ℝ, a>0, a≠1) logaritmusfüggvényt mint az
y=ax : ℝ → ℝ+ (a∈ℝ, a>0, a≠1)
exponenciális függvény inverz függvényét. Vagyis x=loga(y) az a valós szám, amelyre
y = aloga(y)
teljesül minden y∈ℝ+ pozitív valós számra.
Az f(x)=ln(x)=loge(x) : ℝ+ → ℝ függvényt, ahol
e≈2,718281828
az ún. Euler-féle szám
(a természetes logaritmus alapszáma),
természetes alapú logaritmusfüggvénynek nevezzük.
A függvény görbéje:
Az ex exponenciális függvény és az ln(x) természetes alapú logaritmusfüggvény görbéje együtt ábrázolva (feltüntetve az y=x lineárs függvény görbéjét is):
A logaritmusfüggvényre vonatkozó fontosabb azonosságok:
loga(1) = 0
loga(a) = 1
loga(a2) = 2
...
loga(an) = n (n∈ℕ)
loga(x*y) = loga(x) + loga(y)
loga(x/y) = loga(x) − loga(y)
loga(xn) = n*loga(x) (n∈ℕ)
logb(x) = loga(x) / loga(b)
Az exponenciális függvényt és a természetes alapú logaritmusfüggvényt együtt ábrázoló diagramon megfigyelhetjük, hogy a két függvény grafikonja szimmetrikus az y=x függvény grafikonjára.
Általánosan megfogalmazva: ha az f : ℝ → ℝ valós függvény invertálható (azaz létezik az
f−1 : ℝ → ℝ
inverz függvény),
akkor az f(x) függvény és az f−1(x) inverz függvény grafikonjai az y=x függvény grafikonjára, azaz
a koordináta-rendszer x tengelyével 45°-os szöget bezáró egyenesre nézve
tengelyszimmetrikusak. Például
– az f(x)=ex exponenciális és az f−1(x)=ln(x) természetes alapú logaritmusfüggvény,
– a nemnegatív valós számok körében az f(x)=x2 és az f−1(x)=√x négyzetgyökfüggvény,
– az f(x)=f−1(x)=1/x függvény (amelynek az inverze önmaga),
– az f(x)=2*x és az f−1(x)=0.5*x lineáris függvények stb.
ilyen tulajdonságúak.
(Egy P(x,y) pontot az y=x egyenesre tükrözve a pont képe a P'(y,x) pont lesz. Tehát az f(x) függvény bármely Q(x,f(x)) pontjának a tükörképe Q'(f(x),x), és ez
f−1(f(x))=x
miatt rajta van az f−1(x) függvény grafikonján.)
Ismétlés: Matematika 1, 4. Függvények fogalma, megadási módjai, tulajdonságai.
zérushely:
Azt az x0∈A értéket, amelyre f(x0)=0, az f(x) függvény zérushelyének nevezzük. A zérushely(ek)ben a függvény grafikonja metszi a koordináta-rendszer 'x' tengelyét.
Ha létezik az f(x) valós függvény f−1(x) inverz függvénye, és a '0' helyen az inverz függvény értelmezve van, akkor az f(x) függvénynek egy zérushelye van az x0=f−1(0) helyen.
korlátosság:
(a) Az f : A → B valós függvény alulról korlátos, ha van olyan
Ka∈ℝ
szám, amelyre
∀ x∈A ( Ka≤f(x) )
teljesül.
(b) Az f : A → B valós függvény felülről korlátos, ha van olyan
Kf∈ℝ
szám, amelyre
∀ x∈A ( f(x)≤Kf )
teljesül.
(c) Az f : A → B valós függvény korlátos, ha van olyan
K∈ℝ
szám, amelyre
∀ x∈A ( ∣f(x)∣≤K )
teljesül.
Ha az f(x) valós függvény alulról és felülről is korlátos, továbbá alsó korlátja Ka, felső korlátja pedig Kf, akkor az f(x) valós függvény korlátos, egy lehetséges korlátja pedig K = max(∣Ka∣,∣Kf∣). (A bizonyítás azon alapulhat, hogy az így meghatározott K esetén −K ≤ Ka ≤ f(x) ≤ Kf ≤ K teljesül bármely x∈A-ra.)
Ha az f(x) valós függvény korlátos, és korlátja K, akkor alulról és felülről is korlátos. Az f(x) valós függvény egy lehetséges alsó korlátja Ka = −K, egy lehetséges felső korlátja pedig Kf = K.
monotonitás:
(a) Az f : A → B valós függvény az Am⊆A halmazon monoton növekedő, ha
∀x1∈Am ∀x2∈Am
( x1<x2 ⊃ f(x1)≤f(x2) )
teljesül.
(b) Az f : A → B valós függvény az Am⊆A halmazon szigorúan monoton növekedő, ha
∀x1∈Am ∀x2∈Am
( x1<x2 ⊃ f(x1)<f(x2) )
teljesül.
A fentiek alapján definiálhatjuk a valós függvények monoton csökkenő és szigorúan monoton csökkenő tulajdonságait is.
konvexitás:
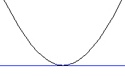
(a) az f valós függvényt egy intervallumon konvexnek ("felfelé görbülőnek") nevezzük, ha az intervallum bármely x1 és x2 helyén teljesül a
f((x1+x2)/2)≤(f(x1)+f(x2))/2
egyenlőtlenség. (Reiman 1992: 492)
Például az f(x)=x2 másodfokú függvény esetében könnyen ellenőrizhető, hogy a fenti egyenlőtlenség az értelmezési tartomány bármely x1 és x2 pontjában teljesül. Szemléletesen ez azt jelenti, hogy a másodfokú függvény bármely pontjában a görbe érintője a görbe alatt helyezkedik el.
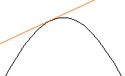
(b) az f valós függvényt egy intervallumon konkávnak ("lefelé görbülőnek") nevezzük, ha az intervallum bármely x1 és x2 helyén teljesül a
f((x1+x2)/2)≥(f(x1)+f(x2))/2
egyenlőtlenség. (Reiman 1992: 492)
Például az f(x)=−x2 másodfokú függvény esetében könnyen ellenőrizhető, hogy a fenti egyenlőtlenség az értelmezési tartomány bármely x1 és x2 pontjában teljesül. Szemléletesen ez azt jelenti, hogy a másodfokú függvény bármely pontjában a görbe érintője a görbe felett helyezkedik el.
(c) Ha az f(x) függvény egy x=a pontban görbületet vált, az 'a' pontot az f(x) függvény inflexiós pontjának nevezzük.
Például az x=0 pont az f(x)=x3 harmadfokú függvény inflexiós pontja.
szélsőértékek:
(a) Az f : A → B valós függvénynek az As⊆A halmazon lokális minimuma van, ha létezik olyan xmin∈As érték, amelyre
∀x∈As ( f(xmin)≤f(x) )
teljesül. Az xmin értéket lokális minimumhelynek, az f(xmin) függvényértéket lokális minimumnak (vagy minimumértéknek) nevezzük.
(b) Az f : A → B valós függvénynek az As⊆A halmazon lokális maximuma van, ha létezik olyan xmax∈As érték, amelyre
∀x∈As ( f(x)≤f(xmax) )
teljesül. Az xmax értéket lokális maximumhelynek, az f(xmax) függvényértéket lokális maximumnak (vagy maximumértéknek) nevezzük.
Ha a fenti definíciók valamelyikében As=A teljesül, abszolút minimumról, ill. abszolút maximumról beszélünk. A minimumhelyeken és maximumhelyeken (az ún. szélsőértékhelyeken) felvett értékeket a függvény szélsőértékeinek nevezzük. A fentiek értelmében beszélhetünk lokális, ill. abszolút szélsőértékhelyekről, ill. szélsőértékekről.
Ha egy f : A → B valós függvénynek az As⊆A halmazon lokális szélsőértéke van, akkor az As⊆A halmazon a függvény alulról, ill. felülről korlátos, és az alsó, ill. felső korlát a függvény adott halmazon felvett szélsőértéke (minimumértéke, ill. maximumértéke).
paritás:
(a) Az f : A → B valós függvény páros, ha
∀x∈A ( −x∈A ⊃ f(−x)=f(x) )
teljesül.
A páros függvények grafikonja (tengelyesen) szimmetrikus a koordináta-rendszer 'y' tengelyére, mivel a függvény értéke az x és −x helyeken megegyezik (feltéve, hogy ezek az értelmezési tartomány elemei).
(b) Az f : A → B valós függvény páratlan, ha
∀x∈A ( −x∈A ⊃ f(−x)=−f(x) )
teljesül.
A páratlan függvények grafikonja (középpontosan vagy centrálisan) szimmetrikus a koordináta-rendszer (0,0) pontjára (az origóra), mivel a függvény értéke az x és −x helyeken egymás ellentettje (feltéve, hogy ezek az értelmezési tartomány elemei).
periodikusság, periodicitás:
Az f : A⊆ℝ → B⊆ℝ valós függvény periodikus, ha létezik olyan p∈ℝ∖{ 0 } zérustól különböző valós szám, amelyre
∀x∈A ( x+p∈A ⊃ f(x)=f(x+p) )
teljesül.
Azt a p∈ℝ+ pozitív valós számot, amelyre a fenti állítás teljesül, a függvény egyik periódusának,
azt legkisebb pτ∈ℝ+ pozitív valós számot pedig, amelyre a fenti állítás teljesül, a függvény (legkisebb) periódusának nevezzük.
(Van olyan periodikus függvény, amelyre pτ∈ℝ+ nem létezik. Ilyen függvények esetében ha p>0 a függvény egyik periódusa, akkor mindig létezik olyan p'>0 másik periódus, amelyre p>p'. Triviális példa az f(x)=c függvény tetszőleges c∈ℝ számra.)
A periodicitás a függvény grafikonján szemléletesen megmutatható például a következőképpen:
(1) a 'p' periódussal rendelkező f(x) függvény grafikonját 'p' távolsággal vízszintesen eltolva (bármelyik irányban) a grafikon önmagába megy át, mivel a függvény értéke az x és az x+p, ill. x−p helyeken megegyezik (feltéve, hogy ezek az értelmezési tartomány elemei);
(2) ha a grafikon 'x' tengelyén kijelölünk egymás után 'p' hosszúságú szakaszokat, a grafikon képe (a görbe "mintázata") ezeken a szakaszokon periodikusan ismétlődik, jellegzetes sormintát képez.
Ha p>0 az f : ℝ → B⊆ℝ valós függvény egyik periódusa és n∈ℤ∖{ 0 } tetszőleges (zérustól különböző) egész szám, akkor n*p szintén az f(x) függvény egyik periódusa. Ha p'>0 az f : ℝ → B⊆ℝ valós függvény egy másik periódusa, akkor p"=p+p' az f(x) függvény egy újabb periódusa.
A tétel első állítása például a következőképpen látható be:
(a) n=1-re az állítás triviális.
(b) n=2-re legyen p>0 f(x) egyik periódusa és x'=x+p.
Ekkor a periodicitás miatt mind f(x)=f(x+p)=f(x'), mind f(x')=f(x'+p) teljesül. Emiatt f(x)=f(x')=f(x'+p)=f((x+p)+p)=f(x+2*p) fennáll, vagyis p'=2*p az f függvény egyik periódusa.
(c) Tegyük fel, hogy a tétel állítása egy n>0 természetes számra igaz. Legyen p>0 f(x) egyik periódusa és x'=x+n*p.
Ekkor a periodicitás miatt mind f(x)=f(x+n*p)=f(x'), mind f(x')=f(x'+p) teljesül. Emiatt f(x)=f(x')=f(x'+p)=f((x+n*p)+p)=f(x+(n+1)*p) fennáll, vagyis p'=(n+1)*p az f függvény egyik periódusa. A teljes indukció elvéből következően tehát a tétel állítása minden természetes számra igaz.
(d) n=−1-re legyen p>0 f egyik periódusa és x=x'+p.
Ekkor f(x)=f(x'+p) és x'=x−p, valamint a periodicitás miatt f(x')=f(x'+p), amiből f(x−p)=f(x')=f(x'+p)=f(x) következik, vagyis p'=−p az f(x) függvény egyik periódusa.
(e) Mivel a tétel állítása minden (pozitív) természetes számra igaz (c pont), és ezek (−1)-szeresére is igaz (d pont), ezért a tétel minden zérustól különböző egész számra igaz.
Néhány valós függvény esetén a fontosabb tulajdonságokat az alábbi táblázatban foglaltuk össze:
| f(x) | Dom(f) | Rng(f) | tulajdonságok |
|---|---|---|---|
| f(x)=∣x∣ | ℝ | ℝ∩[0,+∞) |
zérushely: 0 alsó korlát: 0 abszolút minimumhely: 0 (minimumérték: 0) szigorúan monoton csökken: (−∞,0] szigorúan monoton nő: [0,+∞) páros függvény f(x)→0 (x→0) folytonos: ℝ |
| f(x)=sgn(x) | ℝ | ℝ∩{−1,0,1} |
zérushely: 0 alsó korlát: −1 felső korlát: 1 konstans: f(x)=−1, x∈(−∞,0) konstans: f(x)=1, x∈(0,+∞) páratlan függvény f(x)→−1 (x→0−0) f(x)→1 (x→0+0) x=0 nem megszüntethető szakadási pont (2 nagyságú ugrás) folytonos: ℝ∖{0} |
| f(x)=[x] | ℝ | ℤ | zérushelyek: x∈[0,1) konstans: f(x)=k, x∈[k,k+1) (k∈ℤ) f(x)→k−1 (x→k−0) (k∈ℤ) f(x)→k (x→k+0) (k∈ℤ) x=k (k∈ℤ) nem megszüntethető szakadási pont (1 nagyságú ugrás) folytonos: x∈(k,k+1) (k∈ℤ) jobbról folytonos: x=k (k∈ℤ) |
| f(x)={x} | ℝ | [0,1) | zérushelyek: x=k (k∈ℤ) alsó korlát: 0 felső korlát: 1 abszolút minimumhelyek: x=k (k∈ℤ) (minimumérték: 0) szigorúan monoton nő: x∈[k,k+1) (k∈ℤ) f(x)→1 (x→k−0) (k∈ℤ) f(x)→0 (x→k+0) (k∈ℤ) x=k (k∈ℤ) nem megszüntethető szakadási pont (−1 nagyságú ugrás) folytonos: x∈(k,k+1) (k∈ℤ) jobbról folytonos: x=k (k∈ℤ) |
| f(x)=x | ℝ | ℝ | zérushely: 0 szigorúan monoton nő: ℝ invertálható, f−1(y)=y folytonos: ℝ |
| f(x)=a*x+b (a>0) | ℝ | ℝ | zérushely: −b/a szigorúan monoton nő: ℝ (vö. a>0) invertálható, f−1(y)=(y−b)/a folytonos: ℝ |
| f(x)=x2 | ℝ | ℝ∩[0,+∞) |
zérushely: 0 alsó korlát: 0 abszolút minimumhely: 0 (minimumérték: 0) szigorúan monoton csökken: (−∞,0] szigorúan monoton nő: [0,+∞) páros függvény folytonos: ℝ |
| f(x)=(x+20)*(x−6) | ℝ | ℝ∩[−169,+∞) |
zérushelyek: −20 és 6 alsó korlát: −169 abszolút minimumhely: −7 (minimumérték: −169) szigorúan monoton csökken: (−∞,−7] szigorúan monoton nő: [−7,+∞) páros függvény folytonos: ℝ |
| f(x)=x3 | ℝ | ℝ |
zérushely: 0 szigorúan monoton nő: ℝ páratlan függvény folytonos: ℝ |
| f(x)=1/x | ℝ∖{0} | ℝ∖{0} |
szigorúan monoton csökken: (−∞,0) szigorúan monoton csökken: (0,∞) páratlan függvény f(x)→−∞ (x→0−0) f(x)→∞ (x→0+0) x=0 másodfajú szakadási pont az x=0 egyenes függőleges aszimptota f(x)→0 (x→±∞) az y=0 egyenes vízszintes aszimptota folytonos: ℝ∖{0} |
| f(x)=1/x2 | ℝ∖{0} | ℝ∩(0,∞) |
alsó korlát: 0 szigorúan monoton nő: (−∞,0) szigorúan monoton csökken: (0,∞) páros függvény f(x)→∞ (x→0−0) f(x)→∞ (x→0+0) x=0 másodfajú szakadási pont az x=0 egyenes függőleges aszimptota f(x)→0 (x→±∞) az y=0 egyenes vízszintes aszimptota folytonos: ℝ∖{0} |
| f(x)=√x | ℝ∩[0,+∞) | ℝ∩[0,+∞) |
zérushely: 0 alsó korlát: 0 abszolút minimumhely: 0 (minimumérték: 0) szigorúan monoton nő: [0,+∞) folytonos: ℝ∩[0,+∞) |
| f(x)=3√x | ℝ | ℝ |
szigorúan monoton nő: ℝ páratlan függvény folytonos: ℝ |
| f(x)=sin(x) | ℝ | ℝ∩[−1,1] |
zérushelyek: k*π (k∈ℤ) alsó korlát: −1 felső korlát: 1 abszolút minimumhely: 3*π/2+2*k*π (k∈ℤ) (minimumérték: −1) abszolút maximumhely: π/2+2*k*π (k∈ℤ) (maximumérték: 1) szigorúan monoton csökken: [π/2+2*k*π,3*π/2+2*k*π] (k∈ℤ) szigorúan monoton nő: [−π/2+2*k*π,π/2+2*k*π] (k∈ℤ) periodikus függvény (periódus: 2*π) páratlan függvény folytonos: ℝ |
| f(x)=cos(x) | ℝ | ℝ∩[−1,1] |
zérushelyek: k*π/2 (k∈ℤ) alsó korlát: −1 felső korlát: 1 abszolút minimumhely: π+2*k*π (k∈ℤ) (minimumérték: −1) abszolút maximumhely: 2*k*π (k∈ℤ) (maximumérték: 1) szigorúan monoton csökken: [2*k*π,π+2*k*π] (k∈ℤ) szigorúan monoton nő: [−π+2*k*π,2k*π] (k∈ℤ) periodikus függvény (periódus: 2*π) páros függvény folytonos: ℝ |
| f(x)=1/sin(x) | ℝ∖{k*π|k∈ℤ} | ℝ∖(−1,1) |
zérushelyek: k*π (k∈ℤ) lokális maximumhely: 3*π/2+2*k*π (k∈ℤ) (maximumérték: −1) lokális minimumhely: π/2+2*k*π (k∈ℤ) (minimumérték: 1) szigorúan monoton nő: [π/2+2*k*π,π+2*k*π) és (π+2*k*π,3*π/2+2*k*π] (k∈ℤ) szigorúan monoton csökken: [−π/2+2*k*π,2*k*π) és (2*k*π,π/2+2*k*π] (k∈ℤ) periodikus függvény (periódus: 2*π) páratlan függvény f(x)→−∞ (x→2*k*π−0, k∈ℤ) f(x)→∞ (x→2*k*π+0, k∈ℤ) f(x)→∞ (x→π+2*k*π−0, k∈ℤ) f(x)→−∞ (x→π+2*k*π+0, k∈ℤ) x=k*π (k∈ℤ) másodfajú szakadási pont az x=k*π (k∈ℤ) egyenesek függőleges aszimptoták folytonos: ℝ∖{k*π|k∈ℤ} |
| f(x)=sin(x)/x | ℝ∖{0} | ℝ∩[≅−0.2172,1] |
zérushelyek: k*π (k∈ℤ, k≠0) alsó korlát: ≅−0.2172 felső korlát: 1 abszolút minimumhely: ≅±4.4934 (minimumérték: ≅−0.2172) abszolút maximumhely: 0 (maximumérték: 1) páros függvény f(x)→1 (x→0) (bizonyítás) x=0 megszüntethető szakadási pont folytonos: ℝ∖{0} |
| f(x)=sin(1/x) | ℝ∖{0} | ℝ∩[−1,1] |
zérushelyek: 1/(k*π) (k∈ℤ, k≠0) alsó korlát: −1 felső korlát: 1 abszolút minimumhely: xmin(k)=1/(3*π/2+2*k*π) (k∈ℤ) (minimumérték: −1) abszolút maximumhely: xmax(k)=1/(π/2+2*k*π) (k∈ℤ) (maximumérték: 1) szigorúan monoton csökken: [xmax(k),xmin(k+1)] (k∈ℤ) szigorúan monoton nő: [xmin(k),xmax(k)] (k∈ℤ) páratlan függvény f(x)→−∞ (x→0−0) f(x)→∞ (x→0+0) x=0 másodfajú szakadási pont az x=0 egyenes függőleges aszimptota f(x)→0 (x→±∞) az y=0 egyenes vízszintes aszimptota folytonos: ℝ∖{0} |
| f(x)=tg(x) | ℝ∖{π/2+k*π | k∈ℤ} | ℝ |
zérushelyek: k*π (k∈ℤ) szigorúan monoton nő: (−π/2+k*π,π/2+k*π) (k∈ℤ) periodikus függvény (periódus: π) páratlan függvény f(x)→∞ (x→π/2+k*π−0) (k∈ℤ) f(x)→−∞ (x→π/2+k*π+0) (k∈ℤ) x=π/2+k*π (k∈ℤ) másodfajú szakadási pont az x=π/2+k*π (k∈ℤ) egyenesek függőleges aszimptoták folytonos: ℝ∖{π/2+k*π | k∈ℤ} |
| f(x)=ex | ℝ | ℝ∩(0,+∞) |
alsó korlát: 0 szigorúan monoton nő: (−∞,+∞) invertálható: f−1(y)=ln(y) f(x)→0 (x→−∞) az y=0 egyenes vízszintes aszimptota folytonos: ℝ |
| f(x)=e−x2 | ℝ | ℝ∩(0,+∞) |
alsó korlát: 0 abszolút maximumhely: 0 (maximumérték: 1) szigorúan monoton csökken: (0,∞) szigorúan monoton nő: (−∞,0) páros függvény f(x)→0 (x→−∞) f(x)→0 (x→∞) az y=0 egyenes vízszintes aszimptota folytonos: ℝ |
| f(x)=ln(x) | ℝ∩(0,+∞) | ℝ |
zérushely: 1 szigorúan monoton nő: (0,+∞) invertálható: f−1(y)=ey f(x)→−∞ (x→0) az x=0 egyenes függőleges aszimptota folytonos: ℝ∩(0,+∞) |
Legyenek f : Af⊆ℝ → ℝ és g : Ag⊆ℝ → ℝ valós függvények, és A = Af ∩ Ag. Értelmezzük a függvények között az alábbi műveleteket:
(a) Azt a φ : A⊆ℝ → ℝ valós függvényt, amelyre φ(x)=f(x)+g(x) (x∈A) teljesül, az f(x) és g(x) függvények összegének nevezzük.
(b) Azt a φ : A⊆ℝ → ℝ valós függvényt, amelyre φ(x)=f(x)−g(x) (x∈A) teljesül, az f(x) és g(x) függvények különbségének nevezzük.
(c) Azt a φ : A⊆ℝ → ℝ valós függvényt, amelyre φ(x)=f(x)*g(x) (x∈A) teljesül, az f(x) és g(x) függvények szorzatának nevezzük.
(d) Azt a φ : A∖{ x | g(x)=0 }⊆ℝ → ℝ valós függvényt, amelyre φ(x)=f(x)/g(x) (x∈A) teljesül, az f(x) és g(x) függvények hányadosának nevezzük.
(e) Tegyük fel, hogy Rng(f)⊆Ag teljesül.
Ekkor azt a φ : Af⊆ℝ → ℝ valós függvényt, amelyre
φ(x)=(g∘f)(x)=g(f(x)) (x∈A)
teljesül, a g(x) és f(x) függvények összetett függvényének nevezzük.
Legyenek a,b,c∈ℝ zérustól különböző valós számok. Ekkor az alábbi műveletekkel képzett φ(x) függvény grafikonja előállítható az f(x) függvény grafikonjából ún. függvénytranszformációk segítségével (vö. Obádovics-Szarka 2009: 61-62).
| Ábrázolandó függvény | Függvény képzése | Függvénytranszformáció |
|---|---|---|
| φ(x) = f(−x) | φ(x)=(f∘g)(x), g(x)=−x | f(x) grafikonjának tükrözése a koordináta-rendszer 'y' tengelyére |
| φ(x) = −f(x) | φ(x)=f(x)*g(x), g(x)=−1 | f(x) grafikonjának tükrözése a koordináta-rendszer 'x' tengelyére |
| φ(x) = f(x−a) (a>0) | φ(x)=(f∘g)(x), g(x)=x−a | f(x) grafikonjának eltolása 'a'-val a koordináta-rendszer 'x' tengelye mentén jobbra |
| φ(x) = f(x+a) (a>0) | φ(x)=(f∘g)(x), g(x)=x+a | f(x) grafikonjának eltolása 'a'-val a koordináta-rendszer 'x' tengelye mentén balra |
| φ(x) = f(x)+b (b>0) | φ(x)=f(x)+g(x), g(x)=b | f(x) grafikonjának eltolása 'b'-vel a koordináta-rendszer 'y' tengelye mentén felfelé |
| φ(x) = f(x)−b (b>0) | φ(x)=f(x)−g(x), g(x)=b | f(x) grafikonjának eltolása 'b'-vel a koordináta-rendszer 'y' tengelye mentén lefelé |
| φ(x) = f(c*x) (c>0) | φ(x)=(f∘g)(x), g(x)=c*x |
f(x) grafikonjának c-szeres zsugorítása/nyújtása a koordináta-rendszer 'x' tengelyének irányában (az (x,y)=(0,f(0)) pont rögzített):
– ha |c|>1, akkor zsugorítás vagy összenyomás; – ha |c|<1, akkor nyújtás |
| φ(x) = c*f(x) (c>0) | φ(x)=f(x)*g(x), g(x)=c |
f(x) grafikonjának c-szeres nyújtása/zsugorítása a koordináta-rendszer 'y' tengelyének irányában (az (x,y)=(f−1(0),0) pont rögzített): – ha |c|>1, akkor nyújtás; – ha |c|<1, akkor zsugorítás vagy összenyomás |
Példaként ábrázoljunk az f(x)=x2 függvényből a fenti függvénytranszformációk segítségével előállítható néhány függvényt. A "felfelé nyíló" f(x)=x2, g(x)=(x+40)2 és h(x)=(x+40)2−80 másodfokú függvények (parabolák) görbéi:
A "lefelé nyíló" p(x)=−(x−80)2, q(x)=−(2*x−80)2 és r(x)=−4*(x−80)2, valamint a p(x) függvénynek az 'x' és 'y' tengelyekre tükrözésével kapott pt(x)=(−x−80)2 másodfokú függvények (parabolák) görbéi: