Alkalmazott matematika 2
Tartalom
Sorozatok
Ismétlés:
Matematika 1, 5.1. Sorozatok
Az s : ℕ → ℝ függvényt (végtelen) számsorozatnak nevezzük. A sorozat szokásos jelölése:
s1, s2, ..., sn, ... (n∈ℕ+)
ahol az alsó indexként megadott 1,2,...,n,... értékeket a sorozatelemek indexének nevezzük.
Egyes esetekben a számsorozat elemeinek sorszámozását ("indexelését") 0-tól kezdjük, azaz a sorozatot egy
s : ℕ → ℝ
függvényként definiáljuk, és a sorozat tagjait
s0, s1, ..., sn, ... (n∈ℕ)
módon jelöljük.
Egy s : ℕ → B sorozat
(s1, s2, ..., sn, ...) ∈ B∞
módon is ábrázolható. Jegyezzük meg, hogy a sorozat mint rendezett elemek sorozata és a sorozat elemeiből képzett
{ sn | n∈ℕ }
elemhalmaz különbözik egymástól (például azért, mert egy elemsorozatban az elemek sorrendje is számít; ha pedig az 's' leképezés nem injektív, akkor az sn∈B (n∈ℕ) képelemek között ismétlődő elemek is vannak).
A számsorozatok szokásos megadása általában képlettel, a sorozat általános elemének (sn) a megadásával történik az 'n' index függvényében. Az általános elemet egyes esetekben a megelőző elem vagy elemek segítségével állítjuk elő. Ilyenkor ún. rekurzív definícióról (vagy megadásról) beszélünk. A sorozatok megadásakor egyes esetekben (például rekurzív definíció esetében) szükséges az első elem (s1), és esetleg további elemek megadása is.
Jegyezzük meg, hogy a sorozatok képlettel történő megadása egy algoritmust ad meg, amellyel a sorozat elemei előállíthatók.
Ha a sorozat elemei pozitív számok (azaz sn>0, n∈ℕ) pozitív definit sorozatról, ha pedig negatív számok (azaz sn<0, n∈ℕ), negatív definit sorozatról beszélhetünk. Ha a sorozat elemeinek előjele váltakozik, oszcilláló sorozatról beszélhetünk.
Például adott s1 és 'd' esetén
az
sn=s1+(n−1)*d (n∈ℕ)
sorozatot számtani sorozatnak nevezzük (ahol d∈ℝ a számtani sorozat ún. differenciája). A számtani sorozat elemei rekurzív szabállyal is megadhatók
sn=sn−1+d (n>1)
módon.
A számtani sorozat első 'n' elemének (tagjának) az összege szintén sorozat, amely megadható
Sn=n*(s1+sn)/2=
n*(2*s1+(n-1)*d)/2=
n*s1+n*(n-1)*d/2
módon.
Bizonyítás (teljes indukcióval):
(1) Az Sn=n*(2*s1+(n-1)*d)/2 összefüggés n=1-re (és n=2-re stb.) fennáll.
(2) Tegyük fel, hogy az összefüggés n-re fennáll, azaz Sn=n*(2*s1+(n-1)*d)/2 teljesül.
(3) Ekkor Sn+1=Sn+sn+1 és sn+1=s1+n*d miatt
Sn+1=n*(2*s1+(n-1)*d)/2+sn+1=
n*(2*s1+(n-1)*d)/2+(s1+n*d)=
n*s1+n*(n-1)*d/2+s1+n*d=
(n+1)*s1+n*(n-1)*d/2+2*n*d/2=
(n+1)*s1+((n-1)+2)*n*d/2=
(n+1)*2*s1/2+(n+1)*n*d/2=
(n+1)(2*s1+n*d)/2
vagyis az indukciós feltétel öröklődött n→(n+1)-re, ezért minden természetes számra igaz.
Például adott s1 és 'q' esetén
az
sn=s1*q(n−1) (n∈ℕ)
sorozatot mértani sorozatnak nevezzük (ahol q∈ℝ a mértani sorozat ún. kvóciense). A mértani sorozat elemei rekurzív szabállyal is megadhatók
sn=sn−1*q (n>1)
módon. A mértani sorozat első 'n' elemének (tagjának) az összege szintén sorozat, amely q≠1 esetén megadható
Sn=s1*(qn−1)/(q−1)
módon.
Sorozatok tulajdonságai
Mivel a számsorozatok speciális függvények, értelmezhető rájuk a korábban definiált korlátosság és monotonitás fogalma.
korlátosság
(a) az s : ℕ → ℝ számsorozat alulról korlátos, ha van olyan
Ka∈ℝ
szám, amelyre
∀n∈ℕ (Ka≤sn)
teljesül.
(b) az s : ℕ → ℝ számsorozat felülről korlátos, ha van olyan
Kf∈ℝ
szám, amelyre
∀n∈ℕ (sn≤Kf)
teljesül.
(c) az s : ℕ → ℝ számsorozat korlátos, ha van olyan K szám, amelyre
∀n∈ℕ (∣sn∣≤K)
teljesül.
Például az sn=(2*n−1)/(n+1) sorozat korlátos (vö. Obádovics-Szarka 2009: 268):
– mivel 0<sn (n∈ℕ), ezért Ka=0 alsó korlát;
– Legyen k∈ℝ tetszőleges való szám. Ekkor
sn=(2*n−1)/(n+1)<k ⇔
2*n−1<k*(n+1)=k*n+k ⇔
2*n−k*n=n*(2−k)<k+1
teljesül. Ez k≥2 esetén nyilvánvalóan fennáll
(k=2 esetén 0<3, k>2 esetén pedig n*(2−k)<0<k+1),
vagyis Kf=2 felső korlát.
monotonitás
(a) az s : ℕ → ℝ számsorozat monoton növekedő, ha
∀i∈ℕ ∀j∈ℕ (i<j ⊃ si≤sj)
teljesül.
(b) az s : ℕ → ℝ számsorozat szigorúan monoton növekedő, ha
∀i∈ℕ ∀j∈ℕ (i<j ⊃ si<sj)
teljesül.
(c) az s : ℕ → ℝ számsorozat monoton csökkenő, ha
∀i∈ℕ ∀j∈ℕ (i<j ⊃ si≥sj)
teljesül.
(d) az s : ℕ → ℝ számsorozat szigorúan monoton csökkenő, ha
∀i∈ℕ ∀j∈ℕ (i<j ⊃ si>sj)
teljesül.
Például az
sn=(2*n−1)/(n+1) vagy az
sn=(4*n−9)/(2*n+1)
sorozatok szigorúan monoton növekvőek és korlátosak (vö. Obádovics-Szarka 2009: 269-270).
Sorozatok részsorozatai
Az r : ℕ → ℝ számsorozatot az s : ℕ → ℝ számsorozat részsorozatának nevezzük, ha van olyan
t : ℕ → ℕ
szigorúan monoton növekvő számsorozat (ún. indexsorozat), amelyre
∀n∈ℕ (rn=stn)
teljesül. (Vagyis az sn sorozat egy részsorozata az sn sorozat tn indexű elemeiből áll.)
Tekintsük például az
sn=(−1)n(2*n−1)/(n+1)
sorozatot. Legyen tn=2*n (n∈ℕ), ekkor az sn sorozatból n↔tn helyettesítéssel kapott
rn=stn=
(−1)2*n(2*2*n−1)/(2*n+1)=
(4*n−1)/(2*n+1)
sorozat szigorúan monoton növekvő és korlátos (Kf=2 felső korlát).
Minden s : ℕ → ℝ (végtelen) számsorozatból kiválasztható egy monoton növekedő vagy monoton csökkenő részsorozat. (Farkas 2001: 51-52)
Sorozatok határértéke
(1) Az s : ℕ → ℝ számsorozat határértéke az l∈ℝ szám, ha
∀ε∈ℝ+ ∃nε∈ℕ ∀n∈ℕ ( n≥nε ⊃ ∣sn-l∣<ε )
teljesül. Egyszerűen megfogalmazva: a sorozat elemei egy bizonyos nε indextől kezdődően tetszőlegesen kis ε távolságra megközelítik a sorozat határértékét.
Az ε értéket küszöbértéknek, az nε számot az ε küszöbértékhez tartozó küszöbindexnek nevezzük.
Ha az s : ℕ → ℝ számsorozatnak létezik az l határértéke, akkor konvergensnek nevezzük.
Szemléletesen kifejezve: az l határérték tetszőlegesen kis ε sugarú környezetében az s : ℕ → ℝ számsorozat "majdnem minden" eleme megtalálható (azaz véges sok elem kivételével a sorozat összes eleme).
Azt, hogy az s : ℕ → ℝ számsorozat határértéke az l∈ℝ szám,
lim sn = l
n→∞
(egyszerűbben lim sn = l)
módon jelöljük. Szokásos még az
sn → l (n → ∞)
(egyszerűbben sn → l)
jelölés is.
Például tekintsük azokat az sn sorozatokat, amelyekre teljesül, hogy tetszőleges t∈ℕ+ számhoz hozzá tudunk rendelni egy olyan nt természetes számot, hogy bármilyen n∈ℕ+, n>nt természetes számra
|sn|<1/t
teljesül. Ekkor
sn→0 (n→∞)
teljesül, azaz az így definiált sn sorozatok a 0-hoz konvergálnak. Az ilyen tulajdonságú sorozatokat nullasorozatnak nevezzük (vö. Szendrei 1975: 432). Például az
sn=1/n
sorozat nyilvánvalóan nullasorozat, mivel a szigorúan monoton csökkenés miatt bármely t∈ℕ+ számra nt=t+1 megfelelő lesz küszöbindexnek (ha n>t+1, akkor ebből sn<1/t következik).
A nullasorozat fogalma segítségével azt, hogy egy sn sorozat konvergál egy tetszőleges r∈ℝ számhoz, úgy is kifejezhetjük, hogy az sn sorozat és az
rn=r
konstans sorozat
qn=|sn−rn|
különbsége nullasorozat (azaz qn→0 teljesül). Ekkor az sn sorozat határértékére
sn→r (n→∞)
teljesül.
Ha egy sorozatnak nincs (véges) határértéke, akkor a sorozat divergens.
(2) Egy sorozat konvergenciájára a határérték ismerete nélkül is megadhatunk egy kritériumot.
Az s : ℕ → ℝ (végtelen) számsorozat akkor és csak akkor konvergens, ha
∀ε∈ℝ+ ∃nε∈ℕ ∀m∈ℕ ∀n∈ℕ
( m≥nε ∧ n≥nε ⊃. ∣sm−sn∣<ε )
teljesül (Cauchy-féle kritérium). Szemléletesen megfogalmazva: a sorozat majdnem minden eleme egymástól tetszőlegesen kis távolságra helyezkedik el, "összetorlódik" (vagyis ezek az elemek benne vannak egy közülük választott tetszőleges elem ε sugarú környezetében).
A nullasorozat fogalma segítségével azt, hogy egy sn sorozat Cauchy-sorozat (a fenti értelemben), úgy is kifejezhetjük, hogy az sn sorozat és a sorozat egy tetszőleges
rn
részsorozatának a
qn=|sn−rn|
különbsége nullasorozat (azaz qn→0 teljesül).
(3) Ha az s : ℕ → ℝ számsorozatra teljesül, hogy
∀p∈ℝ ∃np∈ℕ ∀n∈ℕ ( n≥np ⊃ sn>p ),
akkor a sorozat a végtelenhez divergál, amit sokszor úgy fejezünk ki, hogy (általánosított értelemben) a határértéke ∞. Ezt
sn → ∞ vagy
lim sn=∞ módon jelöljük.
Ebben az értelemben beszélhetünk egy divergens sorozat −∞ határértékéről is.
Példák konvergens sorozatokra
(1) Legyen sn=n/(n+1), ekkor lim sn=1.
Legyen 0<ε<1 tetszőlegesen kis pozitív szám. Ekkor 0<sn<1 miatt |sn−1|=|n/(n+1)−1|=1−n/(n+1) teljesül, vagyis
|sn−1|<ε ⇔ 1−n/(n+1)<ε. Az egyenlőtlenség azonos átalakítása után ebből
|sn−1|<ε ⇔
1/(n+1)<ε ⇔
(1/ε−1)<n
adódik. Mivel 0<(1/ε−1) és az egészrész függvény definíciója miatt
0≤[(1/ε−1)]<(1/ε−1)<[(1/ε−1)]+1 teljesül, ha az Nε küszöbindexet
Nε=[(1/ε−1)]+1
módon választjuk meg, akkor minden Nε<n számra
|sn−1|<ε teljesül, vagyis definíció szerint
lim sn=1.
(2) Legyen sn=−2*n/(n+1), ekkor lim sn=−2.
(3) Legyen sn=(4*n-1)/(n+5), ekkor lim sn=4.
(4) Az sn=1/n sorozat (szigorúan) monoton csökkenő és korlátos, határértéke lim sn=0.
(5) Az sn=n+10 sorozat nem korlátos, lim sn=∞.
Legyen p∈ℝ tetszőleges valós szám. Ekkor
sn>p ⇔ n+10>p.
Az egyenlőtlenség azonos átalakítása után ebből
sn>p ⇔ n>p−10
következik. Ha tehát az Np küszöbindexet
Np=max{1; [p−10]+1}
módon választjuk meg, akkor n>Np esetén sn>p teljesül, vagyis definíció szerint lim sn=∞.
(6) A
mértani sorozat első 'n' tagjának összegéből képzett S
n sorozat végtelenben vett határértéke |q|<1 esetén létezik, és
lim Sn = s1/(1−q)
n→∞
(az ún.
mértani sor összegképlete).
Elég azt bizonyítanunk, hogy ha |q|<1, akkor az tn=qn sorozat végtelenben vett határértéke 0. |q|<1 miatt |qn+1|<|qn| (n∈ℕ) teljesül, vagyis a |qn| sorozat szigorúan monoton csökkenő. Adott ε>0 esetén válasszuk meg az Nε küszöbindexet úgy, hogy
|qNε|<ε
teljesüljön, ekkor a |qn| sorozat szigorú monoton csökkenése miatt minden n>=Nε természetes számra fenn fog állni a |qn|<ε összefüggés.
Mivel
0<|q|Nε=|qNε|<ε
ezért a logaritmusfüggvény monoton növekedése miatt az egyenlőtlenség ekvivalens az
ln(|q|Nε)<ln(ε)
egyenlőtlenséggel, amiből |q|<1 ⇒ ln(|q|)<0 miatt
Nε>ln(ε)/ln(|q|)
adódik. Ha tehát Nε=[ln(ε)/ln(|q|)]+1, akkor a sorozatok határértékének definíciója alapján
tn→0 (n→∞)
teljesül.
Sorozatok torlódási pontja
A határérték fogalmának általánosítása a torlódási pont (torlódási hely, sűrűsödési hely) fogalma. Az s : ℕ → ℝ számsorozat torlódási pontja az a τ∈ℝ szám, amelynek bármilyen ε>0 sugarú környezete a sorozat végtelen sok elemét tartalmazza.
A határérték definíciójából következik, hogy
(a) egy sorozat határértéke mindig torlódási pont,
és mivel a határérték tetszőleges környezetében benne van a sorozat majdnem minden eleme,
(b) konvergens sorozatnak csak egy torlódási pontja (és egy határértéke) lehet, és
(c) egy konvergens sorozat mindig korlátos.
(b) Tegyük fel, hogy egy számsorozat határértéke (és ezáltal torlódási pontja) l, és létezik egy ettől különböző
τ≠l
torlódási pontja is. Legyen
0<ε<∣τ−l∣/2,
ekkor τ és l ε sugarú környezete diszjunkt, és mivel l ε sugarú környezete a sorozat majdnem minden elemét tartalmazza, τ ε sugarú környezete csak véges elemet tartalmazhat. Emiatt τ nem lehet torlódási pont, ami ellentmondás, tehát nem lehetséges, hogy a sorozatnak van l-től különböző torlódási pontja.
Ha egy sorozatnak egynél több torlódási pontja van, ill. ha nincs torlódási pontja, akkor divergens.
Másrészt ha egy sorozatnak csak egy torlódási pontja van, akkor még nem biztos, hogy konvergens.
Tekintsük például az
|
sn =
| {
| 1/n
| ha 'n' páratlan
|
| n
| ha 'n' páros
|
sorozatot. Ennek egyetlen torlódási pontja τ=0, de nincs határértéke. Vegyük észre, hogy az sn sorozatot két
részsorozat
alkotja:
– páratlan 'n' esetén az n=2*m−1 helyettesítéssel kapott
tm=s2*m−1=1/(2*m−1) (m∈ℕ)
részsorozat, amelyre
tm → 0 (vagyis 0 torlódási pont);
– páros 'n' esetén az n=2*k helyettesítéssel kapott
uk=s2*k=2*k (k∈ℕ)
részsorozat, amelyre
uk → ∞ (megjegyzés: a ∞ nem torlódási pont!).
Egy (végtelen) számsorozat akkor és csak akkor konvergens, ha minden részsorozata konvergens, és a részsorozatok határértéke megegyezik.
A konvergens részsorozatok közös határértéke ekkor megegyezik a sorozat határértékével.
Példa: az sn=(−1)n sorozat divergens.
Az sn=(−1)n két részsorozata a
tk=−1 (k∈ℕ, n=2*k-1) és az
um=1 (m∈ℕ, n=2*m)
sorozat. Mivel
lim tk=−1 és
lim uk=1
miatt a tk és um részsorozatok konvergensek és határértékük különböző, az sn=(−1)n sorozat divergens.
Ha egy sorozat nem korlátos, akkor biztosan divergens.
Korlátos sorozatok konvergenciája
(1) Ha az s : ℕ → ℝ (végtelen) számsorozat monoton növekedő és felülről korlátos, vagy monoton csökkenő és alulról korlátos, akkor az sn sorozat konvergens.
Az A⊂ℝ (valós) számhalmaz felülről korlátos, ha
∃Kf∈ℝ ∀x∈A ( x≤Kf )
teljesül. A Kf számot az A⊂ℝ halmaz felső korlátjának nevezzük.
Az A⊂ℝ felülről korlátos, nem üres valós számhalmaz legkisebb felső korlátja az a
sup A∈ℝ
valós szám, amelyre
∀x∈A ( x≤sup A ) (azaz sup A felső korlát) és
∀ε∈ℝ+ ∃x∈A
( sup A−ε<x )
teljesül. (Megjegyzés: az utóbbi állítás azt fejezi ki, hogy bármilyen kis ε>0 számot veszünk, sup A−ε már nem felső korlát, azaz nem létezik sup A-nál kisebb felső korlát.)
Hasonlóan definiálható egy valós A⊂ℝ számhalmaz alsó korlátja és inf A∈ℝ legnagyobb alsó korlátja.
A legkisebb felső korlát (ill. legnagyobb alsó korlát) korlátos és nem üres valós számhalmazok esetében mindig létezik (vö. Farkas 2001: 34-35).
Ha az s:ℕ→ℝ (végtelen) számsorozat monoton növekedő és felülről korlátos, akkor a sorozat konvergens, és határértéke megegyezik a sorozat elemeiből képzett halmaz legkisebb felső korlátjával, azaz
lim sn=sup { sn | n∈ℕ }
teljesül (vö. Farkas 2001: 61).
Ha az s:ℕ→ℝ (végtelen) számsorozat monoton csökkenő és alulról korlátos, akkor a sorozat konvergens, és határértéke megegyezik a sorozat elemeiből képzett halmaz legnagyobb alsó korlátjával, azaz
lim sn=inf { sn | n∈ℕ }
teljesül (vö. Farkas 2001: 61).
Bizonyíthatóak az alábbi tételek:
(a)
Korlátos (végtelen) számsorozatnak mindig van konvergens részsorozata (Bolzano-Weierstrass tétel; vö. Farkas 2001: 63).
(b)
Az s : ℕ → ℝ (végtelen) számsorozatnak a τ∈ℝ valós szám akkor és csak akkor torlódási pontja, ha létezik az sn sorozatnak τ-hez konvergáló részsorozata (vö. Farkas 2001: 68).
(c)
Korlátos (végtelen) számsorozatnak mindig van torlódási pontja (vö. Farkas 2001: 69).
(2) Egy korlátos (végtelen) számsorozat pontosan akkor konvergens, ha egyetlen torlódási pontja van.
Tegyük fel, hogy egy τ torlódási pont van és a (korlátos) sorozat nem konvergens.
Ekkor a τ torlódási pontnak van olyan környezete, amelyen kívül a sorozatnak
végtelen sok eleme van. A kimaradó elemek a sorozat egy korlátos részsorozatát
alkotják, amelynek a BW tétel szerint van konvergens, és nem τ-hez konvergáló részsorozata.
Emiatt a sorozatnak van τ-től különböző torlódási pontja, ami ellentmondás, mert csak egy torlódási pont lehet.
Műveletek sorozatok között
Legyenek s : ℕ → ℝ, t : ℕ → ℝ és u : ℕ → ℝ (végtelen) számsorozatok. Értelmezzük a sorozatok között az alábbi műveleteket:
(a) Az sn és tn számsorozat összegének nevezzük azt az un számsorozatot, amelynek elemeire
un=sn+tn (n∈ℕ)
teljesül.
(b) Az sn és tn számsorozat különbségének nevezzük azt az un számsorozatot, amelynek elemeire
un=sn−tn (n∈ℕ)
teljesül.
(c) Az sn és tn számsorozat szorzatának nevezzük azt az un számsorozatot, amelynek elemeire
un=sn*tn (n∈ℕ)
teljesül.
(d) Legyen t : ℕ → ℝ olyan számsorozat, amelyre tn≠0 (n∈ℕ) teljesül.
Ekkor az sn és tn számsorozat hányadosának nevezzük azt az un számsorozatot, amelynek elemeire
un=sn/tn (n∈ℕ)
teljesül.
Sorozatok határértékére vonatkozó fontosabb tételek
(I) Konvergens sorozatokra vonatkozó tételek
Legyenek s : ℕ → ℝ és t : ℕ → ℝ (végtelen) számsorozatok. Ekkor teljesülnek az alábbi állítások:
(a.1) Ha az sn sorozat konvergens, akkor az ∣sn∣ sorozat is konvergens, és
lim ∣sn∣=∣lim sn∣.
(a.2) Ha az sn és tn sorozatok konvergensek, akkor összegük is konvergens, és
lim (sn+tn)=(lim sn)+(lim tn).
(a.3) Ha az sn és tn sorozatok konvergensek, akkor különbségük is konvergens, és
lim (sn−tn)=(lim sn)−(lim tn).
(a.4) Ha az sn sorozat konvergens és c∈ℝ tetszőleges valós szám, akkor a c*sn sorozat is konvergens, és
lim (c*sn)=c*lim sn.
(a.5) Ha az sn és tn sorozatok konvergensek, akkor szorzatuk is konvergens, és
lim (sn*tn)=(lim sn)*(lim tn).
(a.6) Ha az sn és tn sorozatok konvergensek, tn≠0 (n∈ℕ) és lim tn≠0, akkor hányadosuk is konvergens, és
lim (sn/tn)=(lim sn)/(lim tn).
(a.7) Legyenek s : ℕ → ℝ, t : ℕ → ℝ és u : ℕ → ℝ (végtelen) számsorozatok. Ekkor
ha az sn és tn sorozatok konvergensek és határértékük megegyezik, azaz
lim sn=lim tn=l,
valamint
sn<un<tn (n∈ℕ)
teljesül, akkor az un sorozat is konvergens, és lim un=l.
(Ez az ún. csendőrszabály.)
(II) Divergens sorozatokra vonatkozó tételek
Legyenek s : ℕ → ℝ, t : ℕ → ℝ és u : ℕ → ℝ (végtelen) számsorozatok. Ekkor teljesülnek az alábbi állítások:
(b.1) ha lim sn=∞, akkor lim ∣sn∣=∞ teljesül.
(b.2) ha lim sn=∞ és c>0 valós szám, akkor lim c*sn=∞ teljesül.
(b.3) ha lim sn=∞ és c<0 valós szám, akkor lim c*sn=−∞ teljesül.
(b.4) ha lim sn=∞ és a tn sorozat
alulról korlátos, és van olyan Ka>0 valós szám, amelyre tn>Ka (n∈ℕ) teljesül, akkor
lim sn*tn=∞ teljesül.
(b.5) ha az sn sorozat
alulról korlátos,
és van olyan Ka>0 valós szám, amelyre sn>Ka (n∈ℕ), valamint
lim tn=0 és
tn≠0 (n∈ℕ) teljesül, akkor
lim ∣sn/tn∣=∞ teljesül.
(b.6) ha az sn sorozat
korlátos,
azaz van olyan K≥0 valós szám, amelyre ∣sn∣≤K (n∈ℕ), valamint
lim tn=∞ teljesül, akkor
lim sn/tn=0 teljesül.
Például határozzuk meg az
sn=(2*n−1)/(n+1)
sorozat határértékét. Azonos átalakítással
sn=(2−1/n)/(1+1/n)
adódik. Mivel (b.6) miatt
tn=1/n → 0 (n → ∞),
(a.2), (a.3) és (a.6) miatt
lim sn=2/1=2
n→∞
teljesül, vagyis a sorozat konvergens és határértéke 2.
Ábrázoljuk az alábbi sorozatokat, ha szükséges, határozzuk meg a sorozat általános elemét, írjuk fel az első 10 elemet, vizsgáljuk a sorozatokat monotonitás és korlátosság szempontjából, és határozzuk meg a sorozatok határértékét! (vö. Reiman 1992: 413-414, Veressné 1996: 35)
Ha a sorozatok első 'n' elemét konkrétan meg akarjuk határozni, érdemes egy olyan programot írni, amely kiszámolja a sorozat elemeit. Például használhatjuk az alábbi online JavaScript interpretert:
Online JavaScript Interpreter by Peter Jipsen, Chapman University (January 2013).
http://math.chapman.edu/~jipsen/js/ (2019-11-23)
Megjegyzés:
Ha a fenti link valamilyen oknál fogva nem működik, használjuk az
alábbi linket.
Legyen az sn sorozat első 4 eleme a következő:
| n
| 1
| 2
| 3
| 4
| ...
|
| sn
| 3
| 6
| 9
| 12
| ...
|
A sorozat első 10 elemét például a következő programmal írathatjuk ki:
writeln("s(n) = 3*n");
writeln();
for(var n=1;n<=10;n++) {
var s=3*n;
writeln(n+". elem: "+s);
}
writeln("-----");
Legyen az sn sorozat első 4 eleme a következő:
| n
| 1
| 2
| 3
| 4
| ...
|
| sn
| 3
| 6
| 12
| 24
| ...
|
Legyen az sn sorozat első 4 eleme a következő:
| n
| 1
| 2
| 3
| 4
| ...
|
| sn
| 1
| 4
| 9
| 16
| ...
|
Legyen az sn sorozat első 4 eleme a következő:
0, 1/2, 2/3, 3/4, ...
A sorozat első 10 elemét például a következő programmal írathatjuk ki:
writeln("s(n) = (n-1)/n");
writeln();
for(var n=1;n<=10;n++) {
var s=(n-1)/n;
writeln(n+". elem: "+s.toFixed(8));
}
writeln("-----");
Egy másik megoldás:
writeln("s(n) = (n-1)/n");
writeln();
writeln("1. elem: 0");
for(var n=2;n<=10;n++) {
var s=(n-1)/n;
writeln(n+". elem: "+(n-1)+"/"+n);
}
writeln("-----");
Legyen az sn sorozat első 5 eleme a következő (Fibonacci-sorozat):
1, 1, 2, 3, 5, ...
A sorozat első 10 elemét például a következő programmal írathatjuk ki:
writeln("s(n) = s(n-2)+s(n-1)");
writeln();
var s1=1;
var s2=1;
writeln("1. elem: "+s1);
writeln("2. elem: "+s2);
for(var n=3;n<=10;n++) {
var s=s1+s2;
writeln(n+". elem: "+s);
s2=s1;
s1=s;
}
writeln("-----");
1, 2, 4, 7, 11, 16, ...
1, 2, 4, 8, 16, 32, ...
sn=−(n+1)/n
sn=n/(5*n+2)
sn=2−1/n
sn=(3*n2−5*n+6)/(2*n2+n+1)
sn=(−1)n/n3
sn=sin(n*π/2)
s1=0, s2=1,
sn=(sn−1+sn−2)/2 (n≥3)
Keressük az
sn=c1*sn−1+c2*sn−2 rekurzív képlettel megadott sorozat általános elemét
sn=λ*x1n+μ*x2n (λ,μ∈ℝ)
alakban, ahol x1 és x2 az
x2−c1*x−c2=0
másodfokú egyenlet gyökei (vö. Reiman 1992: 417). A feladatban szereplő rekurzív képlet alapján c1=c2=1/2, tehát a másodfokú egyenlet (a sorozat ún. karakterisztikus egyenlete)
x2−x/2−1/2=0
alakú. Az egyenletet a gyökképlettel megoldva az egyenlet gyökei
x1=1 és x2=−1/2
lesznek, tehát a sorozat n-ik eleme
sn=λ+μ*(−1/2)n (λ,μ∈ℝ) (n≥3)
alakú. Mivel a0=0 és a1=1, ebből a λ és μ számokra az
a0=λ−μ/2=0 és
a1=λ+μ/4=1
egyenleteket írhatjuk fel. Ezeket megoldva λ=2/3 és μ=4/3 adódik, vagyis a sorozat általános eleme
sn=2/3+4/3*(−1/2)n
amiből egyebek közt az is jól látszik, hogy a sorozat konvergens, és határértéke sn→2/3 (n→∞).
s1=5, s2=−1,
sn+1=(sn−1+sn)/2 (n>1)
Függvények határértéke
Foglalkozzunk a továbbiakban egyváltozós valós függvényekkel.
Az f : A⊆ℝ → ℝ valós függvénynek az értelmezési tartomány egy a∈A pontjában vett δ>0 sugarú környezete alatt a
Ka,δ={x∈A | |x−a|<δ}
számhalmazt értjük. Egyes esetekben a környezetből kivesszük az 'a' számot, ekkor a
K(a),δ={x∈A | x≠a, |x−a|<δ}=
Ka,δ∖{a}
környezetet kapjuk. Ilyenkor ún. pontozott környezetről beszélhetünk (vö. Császár 1983: 155).
A későbbiekben fontos lesz a baloldali környezet és a jobboldali környezet fogalma is.
Az f : A⊆ℝ → ℝ valós függvénynek az értelmezési tartomány egy a∈A pontjában vett δ>0 sugarú (pontozott) baloldali környezete alatt az
La,δ={x∈A | a−δ<x≤a} =
Ka,δ∩(−∞,a]
L(a),δ{x∈A | a−δ<x<a} =
Ka,δ∩(−∞,a) =
K(a),δ∩(−∞,a]
számhalmazokat értjük.
Hasonlóan, az f : A⊆ℝ → ℝ valós függvénynek az értelmezési tartomány egy a∈A pontjában vett δ>0 sugarú (pontozott) jobboldali környezete alatt a
Ra,δ={x∈A | a≤x<a+δ} =
Ka,δ∩[a,+∞)
R(a),δ={x∈A | a<x<a+δ} =
Ka,δ∩(a,+∞) =
K(a),δ∩[a,+∞)
számhalmazokat értjük.
A környezet fogalmát kiterjeszthetjük a végtelenre is. A (plusz) végtelen δ sugarú környezete alatt a
K(∞),δ={x∈A | δ<x}
környezetet, a minusz végtelen δ sugarú környezete alatt pedig a
K(−∞),δ={x∈A | x<δ}
környezetet értjük.
x∈Ka,δ definíció szerint pontosan akkor teljesül, ha
|x−a|<δ
teljesül. Ez az abszolút érték definíciója miatt
x≥a esetén x−a<δ ⇔ x<a+δ
x<a esetén a−x<δ ⇔ a−δ<x
teljesülését jelenti. Ebből következik, hogy
x∈Ka,δ pontosan akkor teljesül, ha
a−δ<x<a+δ
teljesül.
Ezt átalakítva
x∈Ka,δ pontosan akkor teljesül, ha
−δ<x−a<δ
teljesül.
Megjegyzés: a
−δ<(x−a)<δ
egyenlőtlenség ekvivalens a
−δ<(a−x)<δ
egyenlőtlenséggel.
(I.) Legyen f : A⊆ℝ → ℝ valós függvény, és a∈A az értelmezési tartomány egy pontja, amelynek egy környezetében a függvény értelmezve van.
(Ha az f(x) függvény nem értelmezett az a∈ℝ pontban, akkor tegyük fel, hogy az 'a' pont egy pontozott környezetében a függvény értelmezve van.(0))
Az f : A⊆ℝ → ℝ függvény határértéke az a∈A pontban
lim f(x) = b,
x→a
ha
∀ε>0 ∃δ>0 ∀x∈A
( x≠a ∧
∣x−a∣<δ ⊃.
∣f(x)−b∣<ε )
teljesül. Azt, hogy az f(x) függvény határértéke az a∈A pontban b∈ℝ,
lim f(x)=b (x→a) vagy
f(x)→b (x→a)
módon is jelölhetjük (és ha a kontextusból egyértelmű, az x→a jelölést el is hagyhatjuk).
Szavakban megfogalmazva: ha bármely kis(2) ε>0 esetén meg tudunk adni egy δ>0 küszöbszámot úgy, hogy minden olyan
x∈A (x≠a)(1)
szám esetén, amelyre
a−δ<x<a+δ
teljesül, fennáll a
b−ε<f(x)<b+ε
összefüggés, akkor az f(x) függvény határértéke az x∈A pontban a b∈ℝ szám.
Az f(x) függvény határértéke az 'a' pontban a 'b' szám (azaz f(x)→b (x→a) teljesül), ha teljesül, hogy
–
ha "egyre jobban" (0<δ≪1) megközelítjük az 'x' tengelyen az 'a' számot (vagyis x∈K(a),δ teljesül),
–
akkor az f(x) függvény értéke is "egyre jobban" (0<ε≪1) megközelíti az 'y' tengelyen a 'b' számot (azaz f(x)∈Kb,ε teljesül).
A határérték definíciója úgy fogalmaz, hogy bármilyen kis 0<ε számot választunk, találunk hozzá megfelelő 0<δ küszöbszámot, amelyre a fenti összefüggés fennáll.
A fenti definíció környezetek(3) és sorozatok(4) segítségével is megfogalmazható.
Megjegyzések:
(0) A definícióban itt és a következőkben elég azt feltételezni, hogy az f(x)A⊆ℝ→ℝ valós függvény a vizsgált a∈ℝ pont egy pontozott környezetében értelmezett, azaz van olyan δ>0 szám, hogy
K(a),δ⊆A
teljesül. Mindez a további definíciók esetében is érvényes.
(1) Ha a fenti definícióban x≠a helyett 0<∣x−a∣ vagy ∀x∈A∖{a} szerepel, ekvivalens állításokat kapunk.
Mivel A∖{a}⊂A nyilvánvalóan teljesül, ezért az
F ⇋
∀ε>0 ∃δ>0 ∀x∈A
( ∣x−a∣<δ ⊃.
∣f(x)−b∣<ε )
állításból következik a határérték definíciójában szereplő
H ⇋
∀ε>0 ∃δ>0 ∀x∈A∖{a}
( ∣x−a∣<δ ⊃.
∣f(x)−b∣<ε )
állítás (azaz az állításokra F⊃H teljesül).
(a) Ha tehát egy f(x) függvényre az F állítást bizonyítjuk, abból következik, hogy a függvénynek létezik a határértéke az x=a pontban (például folytonos függvények esetében b=f(a) és az F állítás teljesül).
(b) Ha viszont F nem áll fenn, ebből még nem következik az, hogy nem létezik a határérték. A határérték definíciójában ugyanis megengedjük azt, hogy az f(x) függvény az x=a pontban bármilyen értéket felvegyen, és azt az esetet is, amikor f(x) nem értelmezett az x=a pontban.
(2) Mind az F, mind a H állítások bizonyításakor elegendő kis pozitív ε számokra (pl. 0<ε<1 esetén) megadni a δ(ε) küszöbszámot. Ha ugyanis egy adott ε1 esetén van olyan δ(ε1), amelyre pl.
∀x∈A∖{a}
(∣x−a∣<δ(ε1) ⊃.
∣f(x)−b∣<ε1)
teljesül, akkor bármilyen ennél nagyobb ε1<ε2 esetén a
δ(ε2)=δ(ε1)
küszöbszám nyilvánvalóan megfelelő lesz
∀x∈A∖{a}
(∣x−a∣<δ(ε1)=δ(ε2) ⊃.
∣f(x)−b∣<ε1<ε2)
teljesülése miatt.
(3) A határérték definíciójából következik, hogy ha egy
f : A⊆ℝ → ℝ
függvénynek az értelmezési tartomány egy a∈A pontjában létezik a
lim f(x) = b
x→a
határértéke, akkor a határérték bármely
Kb,ε = { y∈ℝ | ∣y−b∣<ε }
ε sugarú környezetéhez tartozik az a∈A pontnak egy olyan
K(a),δ = { x∈A | x≠a, ∣x−a∣<δ }
δ sugarú környezete,
amelyre
f(K(a),δ) = { f(x) | x∈K(a),δ } ⊆ Kb,ε
teljesül.
Mivel Kb,ε korlátos halmaz, az f(x) függvény korlátos a K(a),δ halmazon.
(4) Egy függvény határértékét ekvivalens módon definiálhatjuk a sorozatok határértéke segítségével is.
Legyen
f : A⊆ℝ → ℝ
valós függvény és a∈A az értelmezési tartomány torlódási pontja. Legyen továbbá
xn : ℕ → A∖{a}
olyan konvergens sorozat, amelynek határértéke
xn → a.
Képezzük az xn sorozatból az
yn=f(xn) sorozatot.
Ekkor megfogalmazhatjuk az alábbi kritériumot: az
f : A⊆ℝ → ℝ
függvénynek akkor és csak van határértéke az a∈A pontban, ha minden fenti módon képzett yn=f(xn) sorozat konvergens és a határértékük megegyezik, azaz létezik olyan b∈ℝ szám, amelyre yn → b teljesül minden yn sorozatra.
A korábbi meghatározásban azt tételeztük fel, hogy a vizsgált a∈ℝ pont egy pontozott környezetében az f(x) függvény értelmezve van. Ekkor az a∈ℝ pont egyszersmind torlódási pont is.
Érdemes kiemelnünk, hogy a "határérték szempontjából az értelmezési tartománynak azok a torlódási helyei figyelemreméltóak, ahol a függvény nincs értelmezve" (Obádovics-Szarka 2009: 69).
Példa: bizonyítsuk be, hogy az f(x)=sin(x)/x függvény határértéke az x=0 pontban f(x)→1, azaz
lim f(x) = 1
x→0
teljesül (vö. Farkas-Fritzné-Kissné 2000: 33-34).
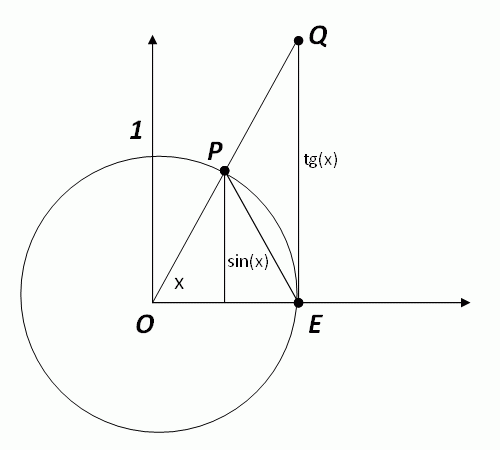
Legyen x∈(0,π/2), ekkor a fenti ábrából leolvasható
az OEP háromszög területe < az OEP körcikk területe < az OEQ háromszög területe
összefüggés, továbbá az r=1 egységsugarú körben fennálló Tkör=r2π=π és
TOEP/Tkör=x/(2*π) ⇒ TOEP=x/2
miatt
sin(x)/2 < x/2 < tg(x)/2 ⇒
sin(x) < x < tg(x) ⇒
1 < x/sin(x) < 1/cos(x) ⇒
cos(x) < sin(x)/x < 1 ⇒
cos(x)−1 < sin(x)/x−1 < 0 ⇒
0 < 1−sin(x)/x < 1−cos(x) (1)
teljesül.
Mivel tetszőleges a∈ℝ szám esetén
0<a<1 ⇒ 0<a2<a<1
teljesül, ezért x∈(0,π/2) esetén sin2+cos2=1 miatt
cos2(x)<cos(x) ⇒
cos2−1(x)<cos(x)−1 ⇒
1−cos(x)<1−cos2(x) ⇒
1−cos(x)<sin2(x)<sin(x) (2)
teljesül.
Mivel az 'x' forgásszöghöz az egységsugarú körben 'x' ívhossz tartozik, az ábrából leolvashatóan x∈(0,π/2) esetén
sin(x)<x (3)
teljesül.
Az (1), (2) és (3) egyenlőtlenségek összekapcsolásával a
0 < 1−sin(x)/x < x
összefüggést kapjuk.
(4)
Mivel x∈(0,π/2) esetén −x<0 nyilvánvalóan teljesül, ezért fennáll a
−x< 1−sin(x)/x < x ⇒
|1−sin(x)/x| < x
összefüggés, amiből x=|x| miatt
|1−sin(x)/x| < |x|
következik. (5)
A (4) összefüggésből −1-gyel való szorzással
0 < 1−sin(x)/x < x ⇒
−x < sin(x)/x−1 < 0
adódik.
Mivel mind az y=sin(x), mind az y=x függvény páratlan, bármely x∈ℝ valós számra
sin(x)/x=sin(−x)/(−x)
teljesül. Ezért a fenti második egyenlőtlenségből x∈(0,π/2) esetén
−x < sin(−x)/(−x)−1 < 0
adódik. Nyilvánvaló, hogy x∈(0,π/2) ⇔ x'=(−x)∈(−π/2,0) fennáll, tehát a fenti egyenlőtlenségből a bármely x'∈(−π/2,0) esetén fennálló
x' < sin(x')/x'−1 < 0
egyenlőtlenséget kapjuk.
Mivel x'∈(−π/2,0) esetén x'=−|x'| és 0<|x'| nyilvánvalóan teljesül, ezért fennáll a
−|x'| < sin(x')/x'−1 < |x'|
egyenlőtlenség, amiből
|sin(x')/x'−1| < |x'|
következik. (6)
Az (5) és (6) esetet összevonva megállapíthatjuk, hogy
x∈(−π/2,π/2)∖{0} esetén
|sin(x)/x−1| = |1−sin(x)/x| < |x|
teljesül. Azonban ebből következően bármilyen ε>0 számra a
δ=min{ε,π/2}
választással
|x−0| = |x| < δ teljesüléséből
|sin(x)/x−1| < |x| < δ ≤ ε adódik,
vagyis a határérték definíciója alapján az
f(x)=sin(x)/x függvényre
lim f(x) = 1
x→0
teljesül.
(II.) Értelmezzük ezek után egy függvény határértékét a végtelenben.
Legyen f : A⊆ℝ → ℝ valós függvény, amelynek A⊆ℝ értelmezési tartománya felülről nem korlátos.
Az f(x) függvény határértéke a végtelenben a b∈ℝ valós szám, azaz
lim f(x) = b,
x→∞
ha
∀ε>0 ∃δ∈ℝ ∀x∈A
( x>δ ⊃
∣f(x)−b∣<ε )
teljesül.
A minusz végtelenben vett határértéket ehhez hasonlóan értelmezhetjük. Ha az f(x) függvény A⊆ℝ értelmezési tartománya alulról nem korlátos, akkor határértéke a minusz végtelenben a b∈ℝ valós szám, azaz
lim f(x) = b,
x→−∞
ha
∀ε>0 ∃δ∈ℝ ∀x∈A
( x<δ ⊃
∣f(x)−b∣<ε )
teljesül.
Például az f(x)=1/x függvény határértéke a végtelenben
1/x→ 0 (x→±∞).
A negatív kitevőjű exponenciális függvény határértéke a végtelenben
e−x → 0 (x→∞).
Az exponenciális függvény határértéke a minusz végtelenben
ex → 0 (x→−∞).
(III.) Értelmezzük most egy függvény végtelen határértékét az értelmezési tartomány egy pontjában.
Legyen f : A⊆ℝ → ℝ valós függvény, a∈A az értelmezési tartomány egy pontja, amelynek egy környezetében a függvény értelmezve van.
(Ha az f(x) függvény nem értelmezett az a∈ℝ pontban, akkor tegyük fel, hogy az 'a' pont egy pontozott környezetében a függvény értelmezve van.)
Az f(x) függvény határértéke az a∈A pontban végtelen, azaz
lim f(x) = ∞,
x→a
ha
∀ε∈ℝ ∃δ>0 ∀x∈A
( x≠a ∧
∣x−a∣<δ ⊃.
f(x)>ε )
teljesül.
Például az f(x)=1/x2 reciprok hatványfüggvény határértéke az x=0 pontban
f(x) → ∞ (x→0).
A minusz végtelenben vett határértéket ehhez hasonlóan értelmezhetjük.
Az f(x) függvény határértéke az a∈A pontban minusz végtelen, azaz
lim f(x) = −∞,
x→a
ha
∀ε∈ℝ ∃δ>0 ∀x∈A
( x≠a ∧
∣x−a∣<δ ⊃.
f(x)<ε )
teljesül.
Végezetül jegyezzük meg, hogy a
lim f(x) = ±∞,
x→±∞
határértékeket a fentiekhez hasonlóan értelmezhetjük.
(IV.) Megfogalmazhatunk egy szükséges és elégséges kritériumot egy függvény (véges) határértékének létezésére vonatkozóan.
Legyen f : A⊆ℝ → ℝ valós függvény, a∈A az értelmezési tartomány egy pontja, amelynek egy környezetében a függvény értelmezve van (megengedjük az a=±∞ lehetőséget is).
(Ha az f(x) függvény nem értelmezett az a∈ℝ pontban, akkor tegyük fel, hogy az 'a' pont egy pontozott környezetében a függvény értelmezve van.)
Az f(x) függvénynek akkor és csak akkor létezik (véges) határértéke az a∈A pontban, ha
∀ε>0 ∃δ>0 ∀x∈A ∀x'∈A
( x∈K(a),δ
∧ x'∈K(a),δ
⊃.
∣f(x)−f(x')∣<ε )
teljesül (Cauchy-féle kritérium).
Például egy adott a∈A pontban a Cauchy-féle kritériumot szavakban a következőképpen fogalmazhatjuk meg:
Ha bármely ε>0 esetén meg tudunk adni egy δ>0 küszöbszámot úgy, hogy tetszőleges olyan
x∈A∖{a} és x'∈A∖{a}
számok esetén, amelyekre
a−δ<x<a+δ és
a−δ<x'<a+δ
teljesül, fennáll a
−ε<|f(x)−f(x')|<ε
összefüggés, akkor az f(x) függvénynek létezik (véges) határértéke az x∈A pontban.
(V.) Végül definiáljuk egy függvény baloldali és jobboldali határértékét.
Legyen f : A⊆ℝ → ℝ valós függvény, a∈A pedig az értelmezési tartomány egy pontja, amelynek egy baloldali környezetében a függvény értelmezve van.
(Ha az f(x) függvény nem értelmezett az a∈ℝ pontban, akkor tegyük fel, hogy az 'a' pont egy pontozott baloldali környezetében a függvény értelmezve van.)
Az f(x) függvény baloldali határértéke az a∈A pontban
lim f(x) = b,
x→a−0
ha
∀ε>0 ∃δ>0 ∀x∈Aa−0
( a−x<δ ⊃
∣f(x)−b∣<ε )
teljesül, ahol
Aa−0 = { x∈A | x<a } = A∩(−∞,a)
az A⊆ℝ értelmezési tartomány leszűkítése az a∈A pontnál kisebb valós számokra.
Szavakban megfogalmazva: ha bármely ε>0 esetén meg tudunk adni egy δ>0 küszöbszámot úgy, hogy minden olyan x∈A (x≠a) szám esetén, amelyre
a−δ<x<a
teljesül, fennáll a
b−ε<f(x)<b+ε
összefüggés, akkor az f(x) függvény baloldali határértéke az x∈A pontban a b∈ℝ szám.
Az f : A⊆ℝ → ℝ valós függvénynek akkor és csak akkor létezik az x=a pontban baloldali határértéke, ha az f(x) függvény
f│A∩(−∞,a)
leszűkítésével kapott függvénynek létezik az x=a pontban határértéke.
Legyen f : A⊆ℝ → ℝ valós függvény, a∈A pedig az értelmezési tartomány egy pontja, amelynek egy jobboldali környezetében a függvény értelmezve van.
(Ha az f(x) függvény nem értelmezett az a∈ℝ pontban, akkor tegyük fel, hogy az 'a' pont egy pontozott jobboldali környezetében a függvény értelmezve van.)
Az f(x) függvény jobboldali határértéke az a∈A pontban
lim f(x) = b,
x→a+0
ha
∀ε>0 ∃δ>0 ∀x∈Aa+0
( x−a<δ ⊃
∣f(x)−b∣<ε )
teljesül, ahol
Aa+0 = { x∈A | x>a } = A∩(a,+∞)
az A⊆ℝ értelmezési tartomány leszűkítése az a∈A pontnál nagyobb valós számokra.
Szavakban megfogalmazva: ha bármely ε>0 esetén meg tudunk adni egy δ>0 küszöbszámot úgy, hogy minden olyan x∈A (x≠a) szám esetén, amelyre
a<x<a+δ
teljesül, fennáll a
b−ε<f(x)<b+ε
összefüggés, akkor az f(x) függvény jobboldali határértéke az x∈A pontban a b∈ℝ szám.
Az f : A⊆ℝ → ℝ valós függvénynek akkor és csak akkor létezik az x=a pontban jobboldali határértéke, ha az f(x) függvény
f│A∩(a,+∞)
leszűkítésével kapott függvénynek létezik az x=a pontban határértéke.
A fentiekhez hasonló módon definiálhatjuk egy függvény végtelen jobboldali és baloldali határértékét az értelmezési tartomány egy pontjában.
Például a tangensfüggvény baloldali határértéke az x=π/2 pontban
tg(x) → ∞ (x→π/2−0).
A tangensfüggvény jobboldali határértéke ugyanebben a pontban
tg(x) → −∞ (x→π/2+0).
Ha egy függvénynek létezik a határértéke egy pontban, továbbá mind a baloldali, mind a jobboldali határérték létezik, akkor ezek értéke megegyezik ebben a pontban.
Megfordítva: ha egy függvénynek létezik a baloldali és a jobboldali határértéke egy pontban és ezek értéke megegyezik, akkor ebben a pontban a függvénynek létezik ezzel megegyező határértéke.
Ebből következően, ha egy függvénynek létezik a baloldali és a jobboldali határértéke egy pontban, és ezek különbözőek, akkor a függvénynek nem létezik határértéke ebben a pontban.
Például az előjel függvény bal oldali határértéke az x=0 pontban −1, jobb oldali határértéke az x=0 pontban +1, vagyis a függvénynek nincs határértéke az x=0 pontban.
Függvények határértékére vonatkozó fontosabb tételek
Legyenek
f : Af⊆ℝ → ℝ és
g : Ag⊆ℝ → ℝ
valós függvények,
A = Af ∩ Ag, és legyenek
az a∈A pont egy környezetében az f(x) és a g(x) függvények értelmezettek.
Ekkor teljesülnek az alábbi állítások:
(a) Ha a
lim f(x) = b
x→a
határérték létezik, akkor
lim ∣f(x)∣ = ∣b∣
x→a
teljesül.
A tétel megfordítása nem igaz (vö. Farkas-Fritzné-Kissné 2000: 28). Azonban ha |f(x)|→0 (x→a) teljesül, akkor ebből a
−|f(x)|≤f(x)≤|f(x)|
egyenlőtlenség és a csendőrszabály miatt f(x)→0 (x→a) már következik.
(b) Ha a
lim f(x) = b
x→a
és a
lim g(x) = c
x→a
határértékek léteznek, akkor
lim (f(x)+g(x)) = b+c
x→a
teljesül.
(c) Ha a
lim f(x) = b
x→a
és a
lim g(x) = c
x→a
határértékek léteznek, akkor
lim (f(x)−g(x)) = b−c
x→a
teljesül.
(d) Ha a
lim f(x) = b
x→a
és a
lim g(x) = c
x→a
határértékek léteznek, akkor
lim (f(x)*g(x)) = b*c
x→a
teljesül.
(d.1) Ha c∈ℝ tetszőleges valós szám és g(x)=c (x∈Ag) a konstans függvény, akkor a (d) tételből
lim (c*f(x)) =
x→a
c*lim (f(x))
x→a
teljesülése következik.
(e) Ha a
lim f(x) = b
x→a
és a
lim g(x) = c
x→a
határértékek léteznek, továbbá c≠0, akkor
lim (f(x)/g(x)) = b/c
x→a
teljesül.
(f) Legyenek
f : Af⊆ℝ → ℝ és
g : Ag⊆ℝ → ℝ
valós függvények,
A = Af ∩ Ag,
és
φ : A⊆ℝ → ℝ
egy valós függvény.
Legyenek az a∈A pont egy
K(a),δ = { x∈A | x≠a ∧ ∣x−a∣<δ }
környezetében az f(x), g(x) és φ(x) függvények értelmezettek, továbbá teljesüljön rájuk az
f(x)≤φ(x)≤g(x) (x∈K(a),δ)
egyenlőtlenség.
Ekkor ha a
lim f(x) = b
x→a
és a
lim g(x) = b
x→a
határértékek léteznek és egyenlők, akkor
lim φ(x) = b
x→a
teljesül. (Ez az ún. csendőrszabály függvények esetén.)
(g) Legyenek
f : Af⊆ℝ → ℝ és
g : Ag⊆ℝ → ℝ
valós függvények, amelyekre
Rng(f)⊆Ag
teljesül (azaz értelmezhető a
φ(x)=(g∘f)(x)=g(f(x))
összetett függvény).
Tételezzük fel, hogy
(g.1) az
af∈Af pont egy környezetében értelmezett az f(x) függvény és
az ag∈Rng(f) pont egy környezetében értelmezett a g(x) függvény, valamint
léteznek a
lim f(x)=ag
x→af
és
lim g(x)=b
x→ag
határértékek;
(g.2) ha a g(x) függvénynek
megszüntethető szakadása
van az
ag∈Ag
pontban (azaz a g(x) függvénynek létezik véges baloldali és jobboldali határértéke az ag pontban, ezek megegyeznek, de különbözőek a függvényértéktől az adott pontban, ha a függvényérték egyáltalán létezik),
akkor van az
af∈Af
pontnak olyan δ>0 sugarú
Kaf,δ =
{x∈Af | x≠af, |x−af|<δ}
(Kaf,δ⊆Af)
környezete, amelyhez tartozó
K' =
{f(x) | x∈Kaf,δ}
(K'⊆Ag)
környezetben nincs benne az
ag
pont, azaz ag∉K' teljesül.
(Ekkor a feltétel bármilyen K⊆Kaf,δ környezethez tartozó K' környezetre is igaz.)
Ekkor a
φ(x)=(g∘f)(x) összetett függvénynek is létezik határértéke, és erre
lim φ(x) = b.
x→af
teljesül.
Példák:
(1) Ha f(x) és g(x) folytonos függvények, a tétel állítása mindig teljesül.
Legyen például f(x)=sin(x)/x (ahol f(0)≐1) és g(x)=ex. Ekkor az
φ(x)=(g∘f)(x)=esin(x)/x
összetett függvénynek létezik határértéke az x=0 pontban, és ez f(x)→1 (x→0), g(x)→e (x→1) miatt
φ(x)→e (x→0).
(2) Ezzel szemben ha f(x)=0 és
g(x)=0 ha x≠0 és
g(x)=1 ha x=0,
akkor az összetett függvény definíciója alapján
φ(x)=(g∘f)(x)=1 ha x≠0 és
φ(x)=(g∘f)(x)=1 ha x=0
teljesül. Ekkor az x=af=0 pontban
f(x)→0,
az x=ag=0 pontban
g(x)→0,
és az x=af=0 pontban
φ(x)=(g∘f)(x)→1(≠0)
teljesül,
vagyis a φ(x)=(g∘f)(x) összetett függvénynek létezik ugyan határértéke az
x=af=0
pontban, de ez nem felel meg a tétel állításának.
Vegyük észre, hogy a problémát az okozta, hogy az f(x) függvény az x=af=0 pont bármilyen kis
Kaf,δ⊆Af
környezetében f(x)=ag=0 értékű, azaz a fenti jelölésekkel ag∈K' (ahol ag=0 a g(x) függvény szakadási pontja).
Emiatt a φ(x)=(g∘f)(x) közvetett függvény az x=af=0 pont bármilyen kis
környezetében felveszi a g(x) függvény szakadási pontban felvett értékét (amely nem egyezik meg a g(x) függvény ag pontban felvett határértékével).
Ezért a φ(x)=(g∘f)(x) közvetett függvény határértéke az af pontban nem egyezik meg a g(x) függvény ag pontban felvett határértékével.
(3) Ha viszont az előző példában f(x)=x (a g(x) függvény pedig ugyanaz, mint korábban), akkor már teljesülnek a tétel feltételei, és
φ(x)=(g∘f)(x)=0 ha x≠0 és
φ(x)=(g∘f)(x)=1 ha x=0
miatt az x=0 pontban
f(x)→0,
g(x)→0 és
φ(x)=(g∘f)(x)→0
teljesül.
Határozza meg az alábbi függvények határértékét (vö. Obádovics-Szarka 2009: 69):
(1.1)
f(x)=x (f(x)→4 ha x→4)
Legyen a függvények határértékére vonatkozó definícióban (pontosabban annak általánosabb alakjában)
A=ℝ, a=4, b=4 és δ=ε, ekkor az
F ⇋
∀ε>0 ∀x∈ℝ
( ∣x−4∣<ε ⊃.
∣f(x)−4∣<ε )
állítás f(x)=x miatt nyilvánvalóan fennáll, vagyis az f(x)=x függvény határértéke az x=4 pontban 4. Mivel egyrészt az x=4 pontban f(x)=4, másrészt pedig látszik, hogy a fenti állítás nemcsak az x=4 pontban, hanem az értelmezési tartomány (ℝ) bármilyen x=a pontjában teljesül, ezért az f(x)=x függvény folytonos az értelmezési tartomány minden pontjában.
(1.2)
f(x)=x2 (f(x)→4 ha x→2; vö. Farkas-Fritzné-Kissné 2000: 30)
Először oldjuk meg az |x2−4|<ε egyenletet 'x'-re az x=2 pont egy környezetében.
(A) Legyen x≥2, ekkor
|x2−4|=x2−4<ε ⇒
x2<ε+4
x<√ε+4
(B) Legyen 0<x<2, ekkor
|x2−4|=4−x2<ε ⇒
x2>4−ε
x>√4−ε (ε≤4)
A megoldásból az (A) esetben
0≤(x−2)<√ε+4−2≐δA
adódik a δA küszöbszámra; a (B) esetben pedig
−x<−√4−ε ⇒
0≤(2−x)<2−√4−ε≐δB
következik a δB küszöbszámra.
Legyen a határérték definíciójának folytonos függvényekre érvényes, "gyengébb" alakjában
A=ℝ,
a=2,
b=4
ε<1
δ=min(√4+ε−2, 2−√4−ε)
ekkor az
F ⇋
∀1>ε>0 ∀x∈ℝ
( ∣x−2∣<δ ⊃.
∣x2−4∣<ε )
állítás |x|≥2 esetén
|x−2|=(x−2)<√4+ε−2 ⇒
|x|<√4+ε ⇒
x2<4+ε ⇒
(x2−4)=|x2−4|<ε
miatt,
0<|x|≤2 esetén pedig
|x−2|=(2−x)<2−√4−ε ⇒
√4−ε<x ⇒
4−ε<x2 ⇒
4−x2=|x2−4|<ε
miatt fennáll,
vagyis az f(x)=x2 függvény határértéke az x=2 pontban 4.
Mivel egyrészt az x=2 pontban f(x)=4, másrészt pedig látszik, hogy a fenti állítás nemcsak az x=2 pontban, hanem az értelmezési tartomány (ℝ) bármilyen x=a pontjában teljesül (pl. a>0 esetén δ=√a*a+ε−a választással), ezért az f(x)=x2 függvény folytonos az értelmezési tartomány minden pontjában.
Megjegyzések:
(1) Könnyen bizonyítható, hogy ε<4 esetén
δA<δB
vagyis
√4+ε−2 < 2−√4−ε
teljesül.
Tehát a δ-ra vonatkozó feltétel miatt
δ=√4+ε−2
mindig jó választás.
Tegyük fel, hogy ε<4 esetén az egyenlőtlenség fennáll, és hajtsunk végre ekvivalens átalakításokat:
√4+ε−2 < 2−√4−ε
√4+ε+√4−ε<4
(4+ε)+(4−ε)+2*√4+ε*√4−ε<16
8+2*√4+ε*√4−ε<16
2*√4+ε*√4−ε<8
√4+ε*√4−ε<4
(4+ε)*(4−ε)<16
16−ε2<16
0<ε2
Ami nyilvánvalóan igaz, tehát az eredeti egyenlőtlenség is teljesül.
(2) Bizonyítható az is, hogy elegendően kis ε érték (pontosabban ε<12) mellett ε/6 < √4+ε−2 teljesül, vagyis δ=ε/6 választás is megfelelő lenne.
(2)
f(x)=x2−2 (f(x)→14 ha x→4; használjuk fel a függvények határértékére vonatkozó (c) és (d) tételeket,
valamint az f(x)=x függvény tulajdonságait)
(3)
f(x)=(x2−3*x+2)/(x2+x−6) (f(x)→1/5 ha x→2; emeljünk ki (x−2)-t)
(4)
f(x)=(x3−3*x−2)/(x2+x−6) (f(x)→9/5 ha x→2; emeljünk ki (x−2)-t)
Osszuk el a számlálóban szereplő (x3−3*x−2) kifejezést (x−2)-vel:
| x3
| −3*x
| −2
| : x−2 =
| x2+2*x+1
|
|
−(x3−2*x2)
|
|
|
|
| 2*x2−3*x−2
|
|
|
|
|
−(2*x2−4*x)
|
|
|
|
|
| x−2
|
|
|
|
|
|
−(x−2)
|
|
|
|
|
| 0
|
|
|
Tehát azt kaptuk, hogy
(x3−3*x−2)=(x−2)*(x2+2*x+1),
és mivel a nevezőben szereplő kifejezés
(x2+x−6)=(x−2)*(x+3)
ezért (x−2)-vel egyszerűsítve már adódik a feladat megoldása.
(5)
f(x)=(3*x−1)/(5*x+2) (f(x)→3/5 ha x→∞; osszuk el a számlálót és a nevezőt 1/x-vel; használjuk fel
az f(x)=1/x függvény tulajdonságait)
(6)
g(x)=(1−cos(x))/x (g(x)→0 ha x→0)
Legyen f(x)=2*x, ekkor a függvények határértékére vonatkozó (g) tétel miatt a φ(x)=(g∘f)(x) összetett függvény határértéke x→0-ban f(x)→0 miatt megegyezik a g(x) függvény határértékével x→0-ban. Mivel a szinusz- és koszinuszfüggvény ismert azonosságai alapján egyrészt
cos(2*x)=cos2(x)−sin2(x), másrészt
sin2(x)+cos2(x)=1, ezért
φ(x)=(1−cos(2*x))/(2*x)=
(sin2(x)+cos2(x)−cos2(x)+sin2(x))/(2*x)=
(2*sin2(x))/(2*x)=
sin(x)*(sin(x)/x)
amiből sin(x)→0 (x→0) és sin(x)/x→1 (x→0) miatt a függvények határértékére vonatkozó (d) tétel alapján φ(x)→0 (x→0), vagyis g(x)→0 (x→0) következik.
(7)
g(x)=sin(4*x)/x (g(x)→4 ha x→0)
(8)
g(x)=(1−cos(x))/x2 (g(x)→1/2 ha x→0)
Függvények folytonossága
Az f : A⊆ℝ → ℝ valós függvény folytonos az x=a pontban, ha
(1) a∈A torlódási pont,
(2) az x=a pontban létezik a véges
lim f(x)
x→a
határérték, és
(3) az x=a pontban a függvény határértéke megegyezik a függvényértékkel, azaz
lim f(x) = f(a)
x→a
teljesül.
A határérték definíciója alapján az f : A⊆ℝ → ℝ valós függvény az értelmezési tartomány a∈A torlódási pontjában folytonos, ha
∀ε>0 ∃δ>0 ∀x∈A
( ∣x−a∣<δ ⊃
∣f(x)−f(a)∣<ε )
teljesül (vegyük észre, hogy az x=a esetet most nem zártuk ki).
Az f : A⊆ℝ → ℝ valós függvény az x=a pontban jobbról folytonos, ha az f(x) függvény
f│A∩[a,∞)
leszűkítésével kapott függvény az x=a pontban folytonos.
Az f : A⊆ℝ → ℝ valós függvény az x=a pontban balról folytonos, ha az f(x) függvény
f│A∩(−∞,a]
leszűkítésével kapott függvény az x=a pontban folytonos.
Legyen f : A⊆ℝ → ℝ valós függvény, és a∈A torlódási pont.
Az f(x) függvénynek az x=a pontban szakadása van (szakadásos), ha ott nem folytonos. Ekkor az x=a pontot szakadási pontnak (szakadási helynek) nevezzük.
A szakadási pontokat például a következőképpen osztályozhatjuk (Farkas-Fritzné-Kissné 2000: 45-46, Obádovics 2011: 70):
(1.1) Az x=a szakadási pont elsőfajú megszüntethető szakadási pont, ha az f(x) függvénynek létezik az a∈A pontban véges baloldali és jobboldali határértéke, ezek megegyeznek, de különbözőek a függvényértéktől az adott pontban (ha a függvényérték egyáltalán létezik):
lim f(x)=b,
x→a−0
lim f(x)=b,
x→a+0
és f(a)≠b vagy f(a) nem létezik
Mivel létezik véges baloldali és jobboldali határérték és ezek megegyeznek, az f(x) függvénynek létezik az x=a pontban véges határértéke, azaz f(x)→b (x→a).
Ha az f(x) függvénynek megszüntethető szakadási pontja van, a függvény egy alkalmas kiterjesztéssel folytonossá tehető; ilyen például a
sin(x)/x
függvény az x=0 helyen.
(1.2) Az x=a szakadási pont elsőfajú, nem megszüntethető szakadási pont, ha az f(x) függvénynek létezik az a∈A pontban véges baloldali és jobboldali határértéke, de ezek nem egyeznek meg:
lim f(x)=b1,
x→a−0
lim f(x)=b2,
x→a+0
b1≠b2
Ebben az esetben az f(x) függvénynek az x=a pontban
c=b2−b1
nagyságú ugrása van.
Például a
sgn(x)
előjelfüggvénynek az x=0 helyen c=2 nagyságú ugrása van.
(2) Az x=a szakadási pont másodfajú szakadási pont, ha az f(x) függvénynek nem létezik véges baloldali vagy jobboldali határértéke. Másodfajú szakadási pontban az f(x) függvénynek nem létezik véges határértéke. (Ha egy f(x) függvénynek egy x=a pontban nem létezik véges határértéke, ún. lényeges szakadási pontról beszélhetünk.)
Például a
sin(1/x)
függvénynek az x=0 helyen nem létezik sem a jobboldali, sem a baloldali határértéke, ezért másodfajú szakadása van. Mivel a sin(1/x) függvény "a 0 pont tetszőleges környezetében minden [−1;1] intervallumbeli értéket felvesz" (vö. Farkas-Fritzné-Kissné 2000: 38), nem létezik véges határértéke az x=0 helyen.
(Például ε=0.5 választás mellett bármilyen δ sugarú környezet esetén létezik olyan 0<|x|, |x'|<δ érték, hogy az f(x)=sin(1/x) függvény értékeire nem teljesül az |f(x)−f(x')|<ε egyenlőtlenség. Ezért ebben a pontban a határértékre vonatkozó Cauchy-féle kritérium alapján az f(x) függvénynek nincs véges határértéke.)
Függvények folytonosságára vonatkozó fontosabb tételek
Legyenek f : A⊆ℝ → ℝ és g : A⊆ℝ → ℝ valós függvények. Ekkor teljesülnek az alábbi állítások:
(a) Ha az f(x) függvény állandó az a∈A pont valamely
Kδ = {x∈A | ∣x−a∣<δ}
környezetében, azaz van olyan c∈ℝ szám, amelyre
f(x)=c (x∈Kδ)
teljesül, akkor az f(x) függvény folytonos az x=a pontban.
(b) Ha az f(x) függvény folytonos az a∈A pontban, akkor az ∣f(x)∣ függvény is folytonos az a∈A pontban.
Bár a tétel a határértékekre vonatkozó (a) tételből is következik, közvetlenül is könnyen belátható az
abszolút érték tulajdonságaiból
következő
∣∣f(x)∣ − ∣f(a)∣∣ ≤ ∣f(x) − f(a)∣
egyenlőtlenség alapján (vö. Farkas 2001: 39, 11.8).
(c) Ha az f(x) és g(x) függvények folytonosak az a∈A pontban, akkor az f(x)+g(x) függvény is folytonos az a∈A pontban.
(d) Ha az f(x) és g(x) függvények folytonosak az a∈A pontban, akkor az f(x)−g(x) függvény is folytonos az a∈A pontban.
(e) Ha az f(x) és g(x) függvények folytonosak az a∈A pontban, akkor az f(x)*g(x) függvény is folytonos az a∈A pontban.
(f) Ha az f(x) és g(x) függvények folytonosak az a∈A pontban és g(a)≠0, akkor az f(x)/g(x) függvény is folytonos az a∈A pontban.
(g) Legyenek
f : Af⊆ℝ → ℝ és
g : Ag⊆ℝ → ℝ
valós függvények, amelyekre
Rng(f)⊆Ag
teljesül.
Ha az f(x) függvény folytonos az a∈Af pontban, és
a g(x) függvény folytonos az
f(a)∈Rng(f)⊆Ag
pontban, akkor a
φ(x)=g(f(x))=(g∘f)(x)
összetett függvény is folytonos az a∈Af pontban.
Vizsgáljuk meg az alábbi függvényeket folytonosság szempontjából (vö. Obádovics 2011: 73):
(1) Legyen
|
f(x) =
| {
| x*sin(1/x)
| ha x≠0
|
| 0
| ha x=0
|
(Igazoljuk, hogy x*sin(1/x)→0 ha x→0 teljesül. Ehhez használjuk fel, hogy x≠0 mellett −1≤sin(1/x)≤1 miatt
−|x|≤|x|*sin(1/x)≤|x| és
−|x|*|sin(1/x)|≤x*sin(1/x)≤|x|*|sin(1/x)|
teljesül.)
(2) Legyen
|
f(x) =
| {
| 4*3x
| ha x<0
|
| x+4
| ha x≥0
|
(3) f(x)=(x3+1)/(x+1)
(tipp: emeljünk ki (x+1)-t!)
(4) f(x)=(3*sin3(x)+cos2(x)+1)/(4*cos(x)−2)
(5) f(x)=cos(x7)
Zárt intervallumban folytonos függvények
Az f : A⊆ℝ → ℝ függvény folytonos, ha f(x) folytonos az A értelmezési tartomány minden a∈A pontjában. Az A⊆ℝ halmazon folytonos függvények halmazát vagy (függvény)osztályát
C0(A)
módon jelöljük.
(Ha I=[a,b] egy zárt intervallum, akkor
C0(I) helyett
C0[a,b]
is írható.)
Legyen f : I⊆ℝ → ℝ valós függvény, I egy tetszőleges (nyílt, félig nyílt, zárt stb.) intervallum. Az f(x) függvény az I intervallumon egyenletesen folytonos, ha
∀ε>0 ∃δ>0 ∀x∈I ∀x'∈I
( ∣x−x'∣<δ ⊃
∣f(x)−f(x')∣<ε )
teljesül. Ha az f(x) függvény az I intervallumon egyenletesen folytonos, akkor az intervallum minden a∈I pontjában folytonos.
(1) Legyen f : I⊆ℝ → ℝ valós függvény, I=[a,b] zárt intervallum,
f∈C0(I)
az I-n folytonos függvény.
Ha f(a)<f(b) teljesül, akkor fennáll a
∀c∈(f(a),f(b)) ∃ξ∈(a,b) ( f(ξ)=c )
összefüggés, vagyis az f(x) folytonos függvény az [a,b] zárt intervallumban minden f(a) és f(b) közé eső értéket felvesz (Bolzano tétele; vö. Farkas-Fritzné-Kissné 2000: 50).
(A tétel igaz f(b)<f(a) teljesülése esetén is egy c∈(f(b),f(a)) értékre.)
(2) Legyen f : I⊆ℝ → ℝ valós függvény, I=[a,b] zárt intervallum, f∈C0(I) az I-n folytonos függvény.
Ekkor
∃K∈ℝ ∀x∈I ( f(x)≤K )
teljesül, vagyis az f(x) folytonos függvény az [a,b] zárt intervallumban korlátos (Weierstrass első tétele; vö. Farkas-Fritzné-Kissné 2000: 51).
(3) Legyen f : I⊆ℝ → ℝ valós függvény, I=[a,b] zárt intervallum, f∈C0(I) az I-n folytonos függvény.
Ekkor
∃ξ∈I ∃η∈I
( f(ξ)=sup{ f(x)|x∈I } ∧
f(η)=inf{ f(x)|x∈I } )
teljesül, vagyis az f(x) folytonos függvény az [a,b] zárt intervallumban felveszi a maximumát és a minimumát (Weierstrass második tétele; vö. Farkas-Fritzné-Kissné 2000: 51-52).
(A tételben szereplő sup{...} és inf{...} jelölések az {...} halmaz legkisebb felső korlátját, ill. legnagyobb alsó korlátját jelölik.)
Legyen f : I⊆ℝ → ℝ valós függvény, I=[a,b] zárt intervallum, f∈C0(I) az I-n folytonos függvény.
Ekkor az f(x) függvény az I zárt intervallumban egyenletesen folytonos.
Ha viszont I egy nem zárt intervallum, akkor már létezik olyan
f∈C0(I)
függvény, amely I-n nem egyenletesen folytonos. Ilyen függvény például f(x)=1/x az I=(0,1) nyílt intervallumon.
Boda István, 2019.