
Ismétlés: Matematika 1, 2.1. Descartes-féle szorzat
Legyen A és B két tetszőleges halmaz, a∈A és b∈B. Ekkor (a,b)-t az 'a' és 'b' elemekből képzett rendezett párnak nevezzük, ahol 'a' az (a,b) rendezett pár első komponense vagy tagja, 'b' pedig az (a,b) rendezett pár második komponense vagy tagja.
Legyenek (a,b) és (c,d) rendezett párok. Ekkor (a,b)=(c,d) akkor és csak akkor teljesül, ha a=c és b=d teljesül, azaz a rendezett párok megfelelő komponensei egyenlők.
Legyen A és B két tetszőleges halmaz. Ekkor az AΧB = { (a,b) | a∈A, b∈B} halmazt, amely az A és B halmazokból képzett rendezett párok halmaza, az A és B halmazok Descartes-féle szorzatának vagy direkt szorzatának nevezzük.
A halmazok megadása rendszerint
{ <halmazelemek> | <logikai feltételek> }
módon történik, ahol a | jel után megadott logikai feltételek alapján az összes olyan, a | jel előtt megadott elemet vagy elemeket keressük, amelyre a feltétel igaz. A vessző (,) jelet a jobb olvashatóság miatt a konjunkció helyett használjuk a logikai feltételben.
Az AΧA direkt szorzatot A2 módon is jelöljük. A direkt szorzat fogalma természetes módon általánosítható 'n' darab halmazra. Az ily módon kapott A1ΧA2Χ ... ΧAn halmaz az A1, A2, ..., An halmazokból képzett rendezett szám n-esek halmaza. Véges Ai halmazok esetén a direkt szorzat elemeinek száma a direkt szorzat tényezőit alkotó halmazok elemszámának szorzata.
A továbbiakban gyakran fogjuk a görög ábécé betűit használni:
Ismétlés: Matematika 1, 2.2. Relációk
Legyen A és B két tetszőleges halmaz. Ekkor az AΧB Descartes-halmaz bármely ρ ⊆ AΧB részhalmazát az A és B halmazok közötti relációnak (megfeleltetésnek) nevezzük.
Ha A = B, akkor a ρ relációt az A-n értelmezett kétváltozós (binér) relációnak nevezzük.
Ha (a,b) ∈ ρ, akkor az 'a' és 'b' elemek relációban vannak egymással. Ezt ρ(a,b) vagy (a ρ b) módon jelöljük.
Minden relációnak egyértelműen megfeleltethető egy logikai függvény. A fent definiált 'ρ' reláció esetén definiáljuk az 'x' és 'y' paraméterektől függő Aρ(x,y) állítást
Aρ(x,y) ⇋ "az x és y elemek relációban vannak egymással, azaz ρ(x,y)"
módon.
Jelöljük azt, hogy az Aρ(x,y) állítás adott x0 és y0 elemekre igaz,
∣Aρ(x0,y0)∣=1
módon.
Ezekkel a jelölésekkel az Aρ(x,y) állítás igazsághalmaza, vagyis azon (x,y) elempárok halmaza, amelyre az állítás teljesül
PAρ = {(x,y) | x∈A, y∈B, |Aρ(x,y)|=1} ⊆ AΧB
megegyezik a ρ relációval, azaz
PAρ=ρ
teljesül.
Példa: definiáljuk a
σ ⊆ ℕΧℕ
oszthatósági relációt
σ = { (a,b) | a∈ℕ, b∈ℕ,
∃n∈ℕ ( b=n*a ) }
módon. A σ reláció mint állítás azt fejezi ki, hogy "az 'a' természetes szám osztója a 'b' természetes számnak" (másképpen "a 'b' természetes szám osztható az 'a' természetes számmal"), amit (a σ b), ill. a megszokott jelöléssel a | b módon jelölhetünk.
Ha egy kétváltozós reláció véges számú elempárból áll (azaz véges számosságú), a reláció megadása legegyszerűbben azoknak az elempároknak a felsorolásával lehetséges, amelyek relációban vannak egymással.
A σ relációt ábrázolhatjuk egy (x,y) koordináta-rendszerben ("rácsban", táblázatban stb.), ahol egy (x,y) pontot akkor és csak akkor jelenítünk meg, ha (x,y)∈σ teljesül. (Egy rácspont megjelenítésére használhatunk pontot, de használhatunk más jeleket, képeket, konkrét (szám)értékeket stb.)
Ha A, B⊆ℕ véges számhalmazok, akkor a σ⊆AΧB relációt egy relációs adatbázis táblájában is megjeleníthetjük úgy, hogy a tábla első oszlopa az 'A' halmaz elemeit, második oszlopa pedig a 'B' halmaz elemeit tartalmazza, a tábla sorai pedig a σ relációban levő számpárokat tartalmazzák.
Például ábrázoljuk a σ(x,y)=x|y relációt a
{2,3,...,10}Χ{2,3,...,10}
számhalmazon egy Excel táblázat segítségével, ahol az 'x' tengely értékeit a táblázat első sorában, az 'y' tengely értékeit függőlegesen, a táblázat első oszlopában adjuk meg. (Azaz az 'x' tengely a bal felső cellától kezdődően balról jobbra, az 'y' tengely pedig a bal felső cellától kezdődően felülről lefelé mutat.)
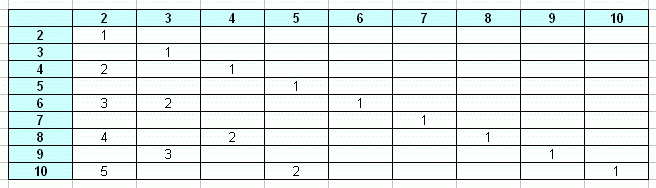
A táblázatban az 'y' tengelyen levő (egész) számok osztóit jelenítjük meg úgy, hogy ha az 'x' tengelyen levő számok osztók, akkor az n=y/x hányados (egész) értékét ábrázoljuk. Például a negyedik oszlop (x=4) nyolcadik cellájában (y=8)
n=y/x=8/4=2
szerepel.
A táblázat sorai megadják az 'y' tengelyen szereplő számok (2...10) osztóit. Figyeljük meg, hogy az 'y' tengelyen levő prímszámoknak megfelelő sorban csak egy oszlopban szerepel 1 (mivel egy prímszámnak az 1-en kívül csak önmaga az osztója, és az 1-gyel való oszthatóságot nem ábrázoltuk).
A táblázat elkészítése:
A {2,3,...,10}Χ{2,3,...,10} halmazra leszűkített σ relációt jelöljük
σ|{2,3,...,10}Χ{2,3,...,10}
módon. A reláció véges számú elemből áll, ezért a relációt alkotó elempárok egy táblázatban (pl. egy relációs adatbázis táblájában) is ábrázolhatók, amely a relációban levő elempárok felsorolásának legkézenfekvőbb módja.
A σ|{2,3,...,10}Χ{2,3,...,10} reláció a következő táblázatban ábrázolható (a harmadik oszlopot csak a könnyebb érthetőség miatt hoztuk létre):
| x | y | y=n*x |
|---|
A táblázat első oszlopában szereplő 'x' értékek a megadott halmazba tartozó 'y' értékek osztói (a triviális 1 osztót leszámítva). A táblázat sort tartalmaz az elvileg lehetséges 81 sorból. Szürkével kiemeltük azokat az n=y/x értékeket, amelyeket korábban az Excel táblázatban ábrázoltunk.
A fenti módon megkonstruált táblázatok és a véges számosságú relációk között egyértelmű megfeleltetés van.
Legyenek A és B véges számosságú halmazok, amelyekre |A|=n, |B|=m (n,m∈ℕ) teljesül. Legyen
ρ ⊆ AΧB
egy tetszőleges reláció. Mivel A és B direkt szorzatának elemszáma
|AΧB|=n*m,
ezért
0≤|ρ|≤n*m
teljesül. A ρ relációt alkotó elempárok ábrázolhatóak egy olyan két oszlopos táblázat soraiban, amelynek az első oszlopában az A halmaz, második oszlopában a B halmaz elemei szerepelnek.
Ez megfordítva is érvényes: minden, a fenti módon megkonstruált táblázat egy relációt ad meg az A és B halmazok között.
Végül jelenítsük meg egy (x,y) koordináta-rendszerben létrehozott rácsban a {2,3,...,10} számok közül azokat, amelyekre teljesül, hogy σ(x,y) vagy (a szokásos jelöléssel) x|y (x,y∈{2,3,...,10}).
A rács koordináta-rendszere abban különbözik a korábbi Excel táblázat koordináta-rendszerétől, hogy a rácsban az 'y' tengely alulról felfelé mutat.
Véges A és B halmazok, továbbá A≠B esetén a
ρ ⊆ AΧB
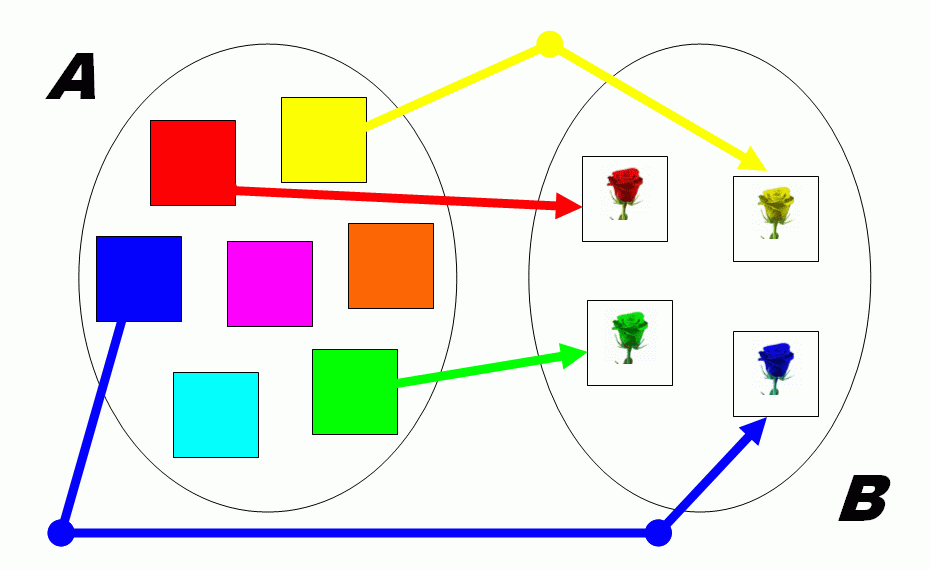
relációt ábrázolhatjuk nyíldiagrammal, ahol az a∈A pontból a b∈B pontba mutató nyilat akkor és csak akkor ábrázoljuk, ha (a,b)∈ρ teljesül. Például legyen A a színek, B a virágok halmaza, és ábrázoljuk a
SZIN ⊆ A={vörös,sárga,kék,...}ΧB={piros_virág,sárga_virág,kék_virág,...}
relációt nyíldiagrammal:
Egy véges A halmaz esetén a ρ ⊆ AΧA binér relációt ábrázolhatjuk egy irányított gráffal, ahol a gráf csúcsai (csúcspontjai, csomópontjai) az A halmaz elemeinek felelnek meg, és az a∈A pontból a b∈A pontba mutató irányított élt (nyilat) akkor és csak akkor ábrázoljuk, ha (a,b)∈ρ teljesül. Ebben az általános értelemben egy G (irányított) gráf az A halmazon értelmezett ρ ⊆ AΧA binér reláció szemléletes leírásának egyik eszköze. (Egy G gráf absztrakt definíciója is ezt fejezi ki, vö. Wikipédia.) Jegyezzük meg, hogy ha a ρ reláció szimmetrikus, akkor a reláció egy irányítatlan gráffal is szemléltethető, ha pedig reflexív, akkor minden csúcsához egy hurokél tartozik.
Tekintsük például az alábbi irányított gráfot:
Az ábrán szereplő gráf alaphalmaza A={1,2,3,4,5,6}, az ábrázolt reláció pedig könnyen ellenőrizhetően ρ={(1,2),(1,4),(2,4),(2,5),(3,6),(4,5),(5,4),(5,5)}.
Feladat: legyen A⊆ℕ a természetes számok egy véges részhalmaza, és ábrázoljuk irányított gráffal a korábban definiált σ oszthatósági reláció szűkítését az A⊆ℕ halmazra.
Ismétlés: Matematika 1, 2.3. Inverz reláció
Legyen A és B két tetszőleges halmaz,
ρ ⊆ AΧB
pedig az A és B halmazok közötti reláció. Ekkor a
ρ-1 ⊆ BΧA =
{ (b,a) | a∈A, b∈B, ρ(a,b) }
relációt a ρ reláció inverz relációjának nevezzük.
Az inverz reláció definíciójából következik, hogy ρ-1(b,a) akkor és csak akkor teljesül, ha ρ(a,b) teljesül. Például a 'tanára' és 'tanítványa' kapcsolatok esetén tanára(a,b) ("'a' tanára 'b' diáknak") akkor és csak akkor teljesül, ha tanítványa(b,a) ("'b' tanítványa 'a' tanárnak") teljesül, ahol 'A' a tanárok, 'B' a diákok halmaza. Természetesen egy tanárnak több tanítványa, és egy diáknak több tanára is lehet.
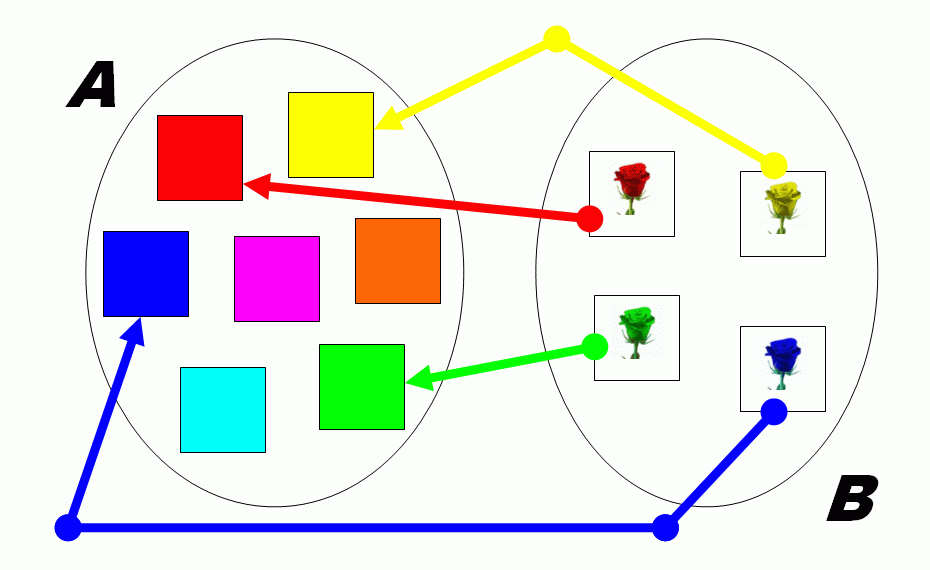
A ρ-1 inverz relációt nyíldiagramon úgy ábrázolhatjuk, hogy a ρ relációt ábrázoló nyíldiagramon a nyilak irányát megfordítjuk. Például az előző SZIN reláció esetében a SZIN-1 inverz reláció a következőképpen ábrázolható:
Ismétlés: Matematika 1, 2.4. A kétváltozós (binér) relációk fontosabb tulajdonságai
(1.1) reflexivitás: a ρ ⊆ AΧA binér relációt reflexívnek nevezzük, ha ∀a ( (a,a)∈ρ ) teljesül. Például az oszthatóság reflexív reláció (minden természetes szám osztója önmagának), és a természetes számokon értelmezett egyenlőség (=) szintén reflexív reláció (minden természetes szám egyenlő önmagával).
(1.2) irreflexivitás: a ρ ⊆ AΧA binér relációt irreflexívnek nevezzük, ha ⌝∃a ( (a,a)∈ρ ), másképpen kifejezve ∀a ( (a,a)∉ρ ) teljesül. Például a "kisebb" (<) vagy "nagyobb" (>) relációk irreflexívek. (Megjegyzés: a "kisebb egyenlő" (≤) és a "nagyobb egyenlő" (≥) relációk azonban már reflexív relációk.)
Vannak olyan relációk, amelyek sem nem reflexívek, sem nem irreflexívek. Például tekintsük az alábbi
η ⊆ ℝΧℝ
binér relációt:
η = {(x,y) | x∈ℝ, y∈ℝ, x2+y2=2}
Könnyen ellenőrizhető, hogy (1,1)∈η és (−1,−1)∈η, vagyis az η reláció nem irreflexív.
Az η reláció minden más (x,y)∈η elemére x≠y teljesül (mivel az y=x egyenes az x2+y2=2 kört csak az (1,1) és (−1,−1) pontokban metszi). Tehát például (0,0)∉η, vagyis az η reláció nem reflexív.
(2.1) szimmetria: a ρ ⊆ AΧA binér relációt szimmetrikusnak nevezzük, ha ∀a ∀b ( (a,b)∈ρ ⊃ (b,a)∈ρ ) teljesül. Például a természetes számokon értelmezett egyenlőség (=) szimmetrikus reláció (ha a,b∈ℕ akkor ha a=b, akkor b=a is teljesül). (Megjegyzés: mivel ∀a∀b ( (a,b)∈ρ ⊃ (b,a)∈ρ ) teljesüléséből ∀a∀b ( (b,a)∈ρ ⊃ (a,b)∈ρ ) következik, ezért a fenti definíció ekvivalens módon megfogalmazható ∀a∀b ( (a,b)∈ρ ≡ (b,a)∈ρ ) vagy (a,b)∈ρ ⇔ (b,a)∈ρ formában.)
(2.2) antiszimmetria: a ρ ⊆ AΧA binér relációt antiszimmetrikusnak nevezzük, ha ∀a∀b ( (a,b)∈ρ ∧ (b,a)∈ρ ⊃. a=b ) teljesül. Például a természetes számokon értelmezett oszthatóság, illetve a "kisebb egyenlő" (≤) és "nagyobb egyenlő" (≥) relációk antiszimmetrikusak.
(2.3) aszimmetria: a ρ ⊆ AΧA binér relációt aszimmetrikusnak nevezzük, ha ∀a∀b ( (a,b)∈ρ ⊃ (b,a)∉ρ ) teljesül. (Az aszimmetria "erősebb" tulajdonság, mint az antiszimmetria abban az értelemben, hogy ha egy reláció aszimmetrikus, akkor biztosan antiszimmetrikus is.) Például a természetes számokon értelmezett "kisebb" (<) és "nagyobb" (>) relációk aszimmetrikusak.
Egy reláció akkor és csak akkor aszimmetrikus, ha antiszimmetrikus és irreflexív.
(3) tranzitivitás: a ρ ⊆ AΧA binér relációt tranzitívnak nevezzük, ha ∀a∀b∀c ( (a,b)∈ρ ∧ (b,c)∈ρ ⊃. (a,c)∈ρ ) teljesül. Például a természetes számokon értelmezett oszthatóság, illetve a "kisebb" (<), "nagyobb" (>), "egyenlő" (=), "kisebb egyenlő" (≤) és "nagyobb egyenlő" (≥) relációk tranzitív relációk.
(4) linearitás vagy trichotómia: a ρ ⊆ AΧA binér relációt lineárisnak vagy trichotomnak nevezzük, ha ∀a∀b ( (a,b)∈ρ ∨ (b,a)∈ρ ∨ a=b ) teljesül. Például a természetes számokon értelmezett "kisebb" (<), "nagyobb" (>), "kisebb egyenlő" (≤) és "nagyobb egyenlő" (≥) relációk lineárisak. (Megjegyzés: a definícióban 'megengedő' vagy szerepel, nem 'kizáró' vagy, vö. Vajda 1996: 36; szigorúbb meghatározás az, hogy a≠b esetén az (a,b)∈ρ és (b,a)∈ρ relációk közül pontosan az egyik teljesül, pl. Bonifert-Kovácsné Győri 1987: 32.)
A trichotómia szemléletes jelentése az, hogy bármely két különböző elem egy trichotom reláció segítségével összehasonlítható.
Foglaljuk össze az irányított gráfokként ábrázolt relációk alapvető tulajdonságait.
| reláció | gráftulajdonság | példák |
|---|---|---|
| reflexív | minden csomóponthoz hurokél tartozik |
– kisebb-egyenlő (≤)
– nagyobb-egyenlő (≥) – osztható (|) – részhalmaz (⊆) |
| irreflexív | egyetlen csomóponthoz sem tartozik hurokél |
– kisebb (<)
– nagyobb (>) – valódi részhalmaz (⊂) |
| egyéb | egyes csomópontokhoz tartozik hurokél, másokhoz nem | |
| szimmetrikus | minden relációban levő csomópontot párhuzamos, ellentétes irányú élek kötnek össze
hurokélek lehetségesek |
nincsenek hurokélek:
– szomszédos minden csomóponthoz hurokél tartozik: – azonos színű – egyenlő (=) |
| antiszimmetrikus | a relációban levő csomópontokat csak egy él köti össze (a gráfban nincsenek párhuzamos, ellentétes irányú élek)
hurokélek lehetségesek |
minden csomóponthoz hurokél tartozik:
– kisebb-egyenlő (≤) – nagyobb-egyenlő (≥) – osztható (|) – részhalmaz (⊆) nincsenek hurokélek (a reláció aszimmetrikus): – kisebb (<) – nagyobb (>) – valódi részhalmaz (⊂) |
| aszimmetrikus | a relációban levő csomópontokat csak egy él köti össze (a gráfban nincsenek párhuzamos, ellentétes irányú élek)
hurokélek nem lehetségesek |
– kisebb (<)
– nagyobb (>) – valódi részhalmaz (⊂) |
| egyéb | egyes relációban levő csomópontokat egy él köt össze, másokat párhuzamos, ellentétes irányú élek kötnek össze
hurokélek lehetségesek | |
| trichotóm | minden csomópontot élek kötnek közvetlenül össze
hurokélek lehetségesek (megengedő trichotómia) ↔ hurokélek nem lehetségesek (szigorú trichotómia) párhuzamos, ellentétes irányú élek lehetségesek (megengedő trichotómia) ↔ párhuzamos, ellentétes irányú élek nem lehetségesek (szigorú trichotómia) |
– egyenlő (=)
– kisebb-egyenlő (≤) – nagyobb-egyenlő (≥) – kisebb (<) – nagyobb (>) |
| nem trichotóm | vannak olyan csomópontok, amelyeket nem kötnek élek közvetlenül össze |
– osztható (|)
– részhalmaz (⊆) – valódi részhalmaz (⊂) |
| tranzitív |
ha egy csomópontból közvetetten, több csomóponton keresztül eljuthatunk egy másik csomópontba, akkor a kiinduló csomópontból közvetlenül is eljuthatunk az utolsó csomópontba mind a közvetett, mind a közvetlen kapcsolatok esetén a csomópontokat összekötő éleknek egy irányba kell mutatnia (az első csomópont felől az utolsó csomópont felé) |
reflexív, szimmetrikus relációk (ekvivalenciarelációk):
– egyenlő (=) reflexív, antiszimmetrikus relációk (rendezési relációk): – kisebb-egyenlő (≤) – nagyobb-egyenlő (≥) – osztható (|) – részhalmaz (⊆) irreflexív, aszimmetrikus relációk (rendezési relációk): – kisebb (<) – nagyobb (>) – valódi részhalmaz (⊂) |
| nem tranzitív | vannak olyan közvetett kapcsolatban levő csomópontok, amelyeket nem kötnek élek közvetlenül össze | |
Ismétlés: Matematika 1, 3.1. Nevezetes kétváltozós relációk: az ekvivalenciareláció
Egyes binér relácókra az eddig megismert tulajdonságok közül néhány együttesen teljesül. Ennek alapján megkülönböztethetjük a binér relációk két fajtáját, az ekvivalenciarelációkat és a rendezési relációkat. Ezeket nevezetes relációknak szokás nevezni.
A ρ ⊆ AΧA binér relációt ekvivalenciarelációnak nevezzük, ha reflexív, szimmetrikus és tranzitív.
A természetes (egész, racionális, valós stb.) számok halmazán értelmezett egyenlőség (=) reláció ekvivalenciareláció.
Egy másik példa ekvivalenciarelációra a következőképpen értelmezett ξ:ℕΧℕ reláció:
ξ={(a,b) | a∈ℕ, b∈ℕ, a≡b (mod 5) }.
A ξ reláció fenti definíciója szerint az adott számmal (esetünkben 5-tel) osztva azonos maradékot adó (azonos maradékosztályba tartozó) természetes számok állnak relációban.
Legyen A egy tetszőleges halmaz,
Η = { A1, A2, ..., An }
pedig az A halmaz nem üres részhalmazainak halmaza, amelyekre teljesül, hogy
(a) Ai⊆A és Ai≠∅ (i=1, 2, ..., n),
(b) a részhalmazok páronként diszjunktak, azaz minden 1 ≤ i≠j ≤ n esetén
Ai ∩ Aj = ∅, és
(c) a részhalmazok uniója magát az A halmazt adja, azaz
A1 ∪ A2 ∪ ... ∪ An = A
teljesül.
Ekkor a Η halmazt A egy osztályozásának nevezzük, az Ai∈Η részhalmazokat (1 ≤ i ≤ n) pedig osztályoknak.
Világos, hogy az A halmaz minden eleme pontosan egy osztályba tartozik.
(a) Legyen ρ ⊆ AΧA egy ekvivalenciareláció, és minden a∈A elemre definiáljuk a Κ(a) = { x∈A | ρ(a,x) } halmazt. Világos, hogy bármely a∈A esetén Κ(a) ⊆ A teljesül, és a ρ reláció reflexivitása miatt a∈Κ(a), vagyis Κ(a) ≠ ∅. Nyilvánvaló, hogy az összes a∈A elemre a Κ(a) részhalmazok uniója az A halmazt adja.
Ha a Κ(a) és Κ(b) halmazoknak van közös eleme, akkor a két halmaz megegyezik.
Tegyük fel, hogy létezik egy olyan x∈A elem, amelyre x∈Κ(a) és x∈Κ(b) teljesül. Ekkor a Κ definíciója szerint ρ(a,x) és ρ(b,x) fennáll.
A ρ reláció szimmetriája miatt ρ(b,x)-ból ρ(x,b) következik, továbbá
a ρ reláció tranzitivitása miatt ρ(a,x) és ρ(x,b)-ből ρ(a,b) következik.
Összegezve: ha a Κ(a) és a Κ(b) halmazoknak van közös eleme, akkor ρ(a,b) teljesül.
Ebből viszont az következik, hogy bármely y∈A elemre, amelyre y∈Κ(a),
y∈Κ(a) ⇒ ρ(a,y) (definíció),
ρ(a,y) ⇒ ρ(y,a) (szimmetria),
ρ(y,a) és ρ(a,b) ⇒ ρ(y,b) (tranzitivitás),
ρ(y,b) ⇒ ρ(b,y) (szimmetria),
ρ(b,y) ⇒ y∈Κ(b) (definíció)
teljesül.
Mivel a fenti gondolatmenet bármely y∈Κ(a) elemre igaz,
Κ(a) ⊆ Κ(b)
teljesül.
Ha pedig ugyanezt a gondolatmenetet egy tetszőleges z∈Κ(b) elemre követjük végig, Κ(b) ⊆ Κ(a) fennállását kapjuk. Ebből viszont a halmazok között értelmezett ⊆ reláció antiszimmetriája miatt
Κ(a) = Κ(b)
következik, vagyis ha a Κ(a) és Κ(b) halmazoknak van közös elemük, a két halmaz egybeesik.
Tehát A bármely két a∈A és b∈A elemére a Κ(a) és a Κ(b) halmazok vagy egybeesnek, vagy diszjunkt halmazok. Ebből következik, hogy az A halmaz részhalmazainak Η = { Κ(a) | a∈A } ⊆ 2A halmaza A egy osztályozását adja. (A Η halmaz minden eleme különböző, mivel egy halmazban nincsenek azonos (ismétlődő) elemek.)
(b) Legyen A egy tetszőleges halmaz,
Η = { A1, A2, ..., An }
pedig ennek egy osztályozása. Definiáljuk a
ρ ⊆ AΧA
binér relációt a következőképpen:
ρ = { (a,b) | ∃ Ai ∈ Η ( a ∈ Ai ∧ b ∈ Ai ) }.
Az így definiált ρ reláció ekvivalenciareláció, ugyanis
(1) mivel Η A egy osztályozása, ezért
∀ a ∈ A ∃! Ai ∈ Η ( a ∈ Ai ).
Mivel azonban
a∈Ai teljesülése esetén
(a∈Ai ∧ a∈Ai)
nyilvánvalóan teljesül, ezért ρ definíciója miatt ρ(a,a) teljesül, vagyis ρ reflexív;
(2) mivel a ρ reláció definíciójában szereplő konjunkció kommutatív, ezért
∀ a ∈ A ∀ b ∈ A ( ρ(a,b) ⊃ ρ(b,a) )
vagyis a ρ reláció szimmetrikus;
(3) ha a ∈ A, b ∈ A és c ∈ A három olyan tetszőleges elem, amelyre ρ(a,b) és ρ(b,c) teljesül, akkor
∃! Ai ∈ Η ( a ∈ Ai ∧ b ∈ Ai ),
valamint
∃! Aj ∈ Η ( b ∈ Aj ∧ c ∈ Aj ),
de mivel
b ∈ Ai ∩ Aj, ezért Ai = Aj,
vagyis ρ(a,c) is fennáll, tehát ρ tranzitív.
Ismétlés: Matematika 1, 3.2. Nevezetes kétváltozós relációk: rendezési relációk
A ρ ⊆ AΧA binér relációt reflexív rendezési relációnak (vagy gyenge rendezési relációnak) nevezzük, ha reflexív, antiszimmetrikus és tranzitív. Például a természetes számokon értelmezett "kisebb egyenlő" (≤) és "nagyobb egyenlő" (≥) relációk reflexív rendezési relációk.
Ha a ρ reflexív rendezési reláció trichotom (lineáris), akkor teljes reflexív rendezési relációnak, ha nem trichotom, akkor parciális reflexív rendezési relációnak nevezzük. Például a korábban bevezetett σ oszthatósági reláció parciális reflexív rendezési reláció. Hasonlóan parciális reflexív rendezési reláció a halmazok között értelmezett ⊆ ("részhalmaza") reláció is.
A σ ⊆ ℕΧℕ oszthatósági reláció parciális reflexív rendezési reláció, azonban ha leszűkítjük a
H = {2, 4, 8, 16, ... } = {2n | n∈ℕ}
halmazra, a σ|H ⊆ HΧH reláció már teljes (trichotom) reláció a H halmazon.
A ρ ⊆ AΧA binér relációt irreflexív rendezési relációnak (vagy szigorú rendezési relációnak) nevezzük, ha irreflexív, aszimmetrikus és tranzitív. Például a természetes számokon értelmezett "kisebb" (<) és "nagyobb" (>) relációk irreflexív (szigorú) rendezési relációk.
Ha a ρ irreflexív rendezési reláció trichotom (lineáris), akkor teljes irreflexív rendezési relációnak, ha nem trichotom, akkor parciális irreflexív rendezési relációnak nevezzük.
Például ha az A véges halmazon értelmezünk egy ρ ⊆ AΧA teljes reflexív (vagy irreflexív) rendezési relációt, akkor egy megfelelő algoritmus segítségével az A halmaz elemei sorba rendezhetők.
Ismétlés: Matematika 1, 4.1. Függvények
Legyen A és B két tetszőleges halmaz, ρ ⊆ AΧB pedig az A és B halmazok közötti reláció. Ekkor a
Dom(ρ) = { a | a∈A, ∃ b∈B ( ρ(a,b) ) }
halmazt a ρ reláció értelmezési tartományának ("indulási halmazának", az "eredeti elemek halmazának"), a
Rng(ρ) = { b | b∈B, ∃ a∈A ( ρ(a,b) ) }
halmazt a ρ reláció értékkészletének (értékhalmazának, "érkezési halmazának", a "képelemek halmazának") nevezzük.
Legyen A és B két tetszőleges halmaz. A ρ ⊆ AΧB relációt hozzárendelésnek nevezzük, ha értelmezési tartománya a teljes A halmaz, azaz Dom(ρ)=A.
Legyen A és B két tetszőleges halmaz. A ρ ⊆ AΧB relációt leképezésnek vagy függvénynek nevezzük, ha
(1) értelmezési tartománya a teljes A halmaz, azaz Dom(ρ)=A (azaz ρ hozzárendelés), és
(2) az értelmezési tartomány minden eleméhez az értékkészlet pontosan egy eleme tartozik, azaz
∀ a∈A ∀ b∈B ∀ b'∈B ( ρ(a,b) ∧ ρ(a,b') ⊃. b=b' )
teljesül.
(Ezt úgy is kifejezhetjük, hogy az értelmezési tartomány minden a∈A elemére ∣{ b | b∈B, ρ(a,b) }∣=1.)
Az A és B halmazokon értelmezett ρ ⊆ AΧB függvény szokásos jelölése f : A → B. Ha az a∈A és b∈B elemekre f(a)=b teljesül, a b∈B elemet az a∈A helyen vett függvényértéknek (vagy helyettesítési értéknek, az a∈A elem "képének") nevezzük.
Ismétlés: Matematika 1, 4.2. Függvények tulajdonságai
injektivitás: az f : A → B függvényt injektívnek vagy kölcsönösen egyértelműnek nevezzük, ha
∀ a∈A ∀ a'∈A ( f(a)=f(a') ⊃ a=a' )
teljesül.
Az injektivitás fenti meghatározása az ( X ⊃ Y ) ~ ( ⌝Y ⊃ ⌝X ) logikai azonosság miatt ekvivalens
∀ a∈A ∀ a'∈A ( a≠a' ⊃ f(a)≠f(a') )
teljesülésével, ami azt fejezi ki, hogy különböző értelmezési tartománybeli elemek képe különböző.
Egy valós függvényt Descartes-féle koordinátarendszerben ábrázolva ez azt jelenti, hogy bármilyen, y=c (c∈ℝ), az 'x' tengellyel párhuzamos egyenesnek a függvény grafikonjával legfeljebb egy közös pontja lehet.
Például az f(x)=3*x+2 függvény injektív, mivel bármely két különböző x1≠x2 számra
f(x1)≠f(x2)
teljesül. Ezzel szemben a g(x)=x2 függvény nem injektív, mert pl.
x1=1 és x2=−1 esetén
g(x1)=g(x2)=1,
vagyis találtunk két olyan különböző
x1≠x2 számot, amelyekre
g(x1)=g(x2)
teljesül. (Megjegyzés: egy állítás cáfolásához elegendő egy ellenpélda!)
szürjektivitás: az f : A → B függvényt szürjektívnek nevezzük, ha Rng(f)=B teljesül (azaz az értékkészlet minden eleme legalább egy értelmezési tartománybeli elem képe).
Például az f(x)=3*x+2 függvény szürjektív, mivel
Rng(f)=ℝ
teljesül. Hasonlóan szürjektív függvény az f(x)=tg(x) függvény.
Ezzel szemben az f(x)=x2 függvény nem szürjektív, mert
Rng(f)=ℝ∩[0,+∞)
teljesül. Nem szürjektívek az f(x)=ex és az f(x)=sin(x) függvények sem.
bijektivitás: az f : A → B függvényt bijektívnek nevezzük, ha injektív és szürjektív.
Ha véges A és B halmazok esetében létezik egy f : A → B bijektív leképezés, akkor elemszámuk megegyezik.
Például az f(x)=3*x+2 függvény bijektív, mert injektív (a függvény különböző értelmezési tartománybeli elemekhez különböző értékeket rendel) és szürjektív (értékkészlete ℝ).
Ismétlés: Matematika 1, 4.3. Inverz függvény, összetett függvény
Legyenek f : Af → B és g : Ag → C tetszőleges függvények, amelyekre Rng(f)⊆Ag teljesül.
Ekkor azt a
h : Af → C függvényt, amelyre teljesül, hogy
az értelmezési tartományának minden x∈Af elemére
h(x)=z akkor és csak akkor teljesül, ha
az
f(x)=y
elemre g(y)=z teljesül,
a g(x) és f(x) függvények összetett függvényének (vagy közvetett függvényének) nevezzük, és
h(x)=(g∘f)(x), vagy egyszerűbben h(x)=g(f(x))
módon jelöljük.
Például ha f(x)=3*x+2 és g(x)=x2 akkor g(x⟷3*x+2) helyettesítéssel h(x)=(g∘f)(x)=g(f(x))=(3*x+2)2 adódik.
Az f : A → B injektív függvény inverz függvénye alatt azt az
f−1 : Rng(f)⊆B → A
függvényt értjük, amelyre teljesül, hogy
az értelmezési tartományának minden y∈Rng(f) elemére
f−1(y)=x akkor és csak akkor teljesül, ha
f(x)=y teljesül.
Jegyezzük meg, hogy ha az f : A → B injektív függvény értékét y=f(x) módon adjuk meg, akkor x∈A és y∈B teljesül. Ugyanilyen jelölésekkel az f(x) inverz függvénye (az értelmezési tartományt némileg leegyszerűsítve) f−1 : B → A alakú, és az inverz függvény értékét x=f−1(y) módon adhatjuk meg. Az inverz függvény esetén az 'y' független változó értékeire y∈B, az 'x' függő változó értékeire pedig x∈A teljesül. Ha egy x0 értékre f(x0)=y0 teljesül, akkor ebből az inverz függvény definíciója miatt f−1(y0)=x0 következik.
Szemléletesen úgy is kifejezhetjük, hogy az f(x) függvény arra ad választ, hogy adott 'x' értékhez milyen f(x)=y függvényérték tartozik; az f−1(y) inverz függvény pedig arra, hogy egy adott 'y' függvényértéket az f(x) függvény milyen x=f−1(y) helyen vesz fel.
Például legyen f(x)=3*x. Ez injektív függvény, amelynek inverzét legegyszerűbben úgy kaphatjuk meg, hogy az y=3*x egyenletet megoldjuk x-re. x=f−1(y)=y/3, tehát az f(x) függvény inverze f−1(y)=y/3. Az x↔y helyettesítés után az inverz függvényre f−1(x)=x/3 adódik.
Az összetett függvény definíciója alapján az f(x) injektív függvényre és f−1(x) inverz függvényére
h(x)=(f−1∘f)(x)=x (x∈A)
teljesül.
Például f(x)=3*x és f−1(x)=x/3 esetén (f−1∘f)(x)=(3*x)/3=x. Egy másik példa: f(x)=ex (x∈ℝ) esetén f−1(x)=ln(x) (x∈ℝ+), és ln(ex)=x teljesül az értelmezési tartomány minden x∈ℝ elemére.
Az inverz függvény definíciójából következik, hogy az inverz függvény az Rng(f) tartományon injektív függvény. Legyen ugyanis y1,y2∈Rng(f) az f−1(y) függvény értelmezési tartományának két különböző eleme (azaz y1≠y2), amelyekre f(x1)=y1 és f(x2)=y2 teljesül (az x1,x2∈A elemek biztosan léteznek, mivel y1 és y2 az f(x) függvény értékkészletének elemei). Az f(x) függvény, tehát x1≠x2 teljesül (egy elemnek ugyanis nem lehet két különböző képe). De mivel definíció szerint f−1(y1)=x1 és f−1(y2)=x2, ebből f−1(y1)≠f−1(y2) következik, tehát az inverz függvény injektív függvény (különböző értelmezési tartománybeli elemek képe különböző).
Az inverz függvényt tetszőleges injektív függvény esetén értelmezzük, ezért az injektív függvényeket invertálható függvényeknek is nevezzük.
Legyen az f(x) függvény invertálható, és inverze az f−1(x) függvény. Ekkor az f−1(x) függvény is invertálható, és inverz függvénye az f(x) függvény, azaz
(f−1)−1(x)=f(x)
teljesül. Emiatt fennáll a
h(x)=(f∘f−1)(x)=x (x∈A)
összefüggés.
Például f(x)=ln(x) (x∈ℝ+), esetén f−1(x)=ex (x∈ℝ), és eln(x)=x teljesül az értelmezési tartomány minden x∈ℝ+ elemére.
Ha az f : A → B függvény bijektív, akkor inverz függvényének értelmezési tartománya B, azaz Dom(f−1)=B, és értékkészlete A, azaz Rng(f−1)=A.
Például az f(x)=3*x+2 függvény bijektív, tehát létezik inverz függvénye. Ez megkapható az y=3*x+2 egyenlőség átrendezésével:
x=f−1(y)=(y−2)/3.
Könnyen ellenőrizhető, hogy
f−1(f(x))=f−1(3*x+2)=((3*x+2)−2)/3=(3*x)/3=x (x∈ℝ), valamint
f(f−1(y))=f((y−2)/3)=3*((y−2)/3)+2=(y−2)+2)=y (y∈ℝ)
teljesül.
A fenti mintapélda lépésről lépésre levezetve:
| lépések | megjegyzések |
|---|---|
| f(x)=3*x+2 | f : ℝ → ℝ invertálható függvény |
| g(x)=f−1(x)=? | feladat az f(x) inverz függvényének meghatározása; keressük azt a g(x) : ℝ → ℝ függvényt, amely az f(x) függvény inverz függvénye |
| y=3*x+2 | az összetartozó (x,f(x))=(x,y)∈ℝΧℝ számpárok alkotják az f(x) függvényt mint relációt |
| x=(y−2)/3 | kifejezzük x-et a szokásos módon (vö. egyenletek ekvivalens átalakításai) |
| f−1(y)=(y−2)/3 | az összetartozó (y,x)=(y,f−1(y))∈ℝΧℝ számpárok alkotják az f−1(x) inverz függvényt mint relációt |
| f−1(x)=(x−2)/3 | végrehajtjuk a formális y↔x helyettesítést (a függvényekben általában 'x' jelöli a független változót) |
| g(x)=(x−2)/3 | megvan a megoldás; most már csak ellenőriznünk kell :-) |
| g(f(x))=? |
ha g(x) valóban f(x) inverz függvénye, akkor g(f(x))=x (vö. az inverz relációnál leírtakkal)
(nyíldiagramon ábrázolva a függvényeket, ez megfelel annak, hogy az f(x)-nek megfelelő nyilakat "megfordítva" kapjuk az x=f−1(y) inverz függvénynek megfelelő nyilakat; ha g(x) az f(x) inverz függvénye, akkor a g(f(x)) közvetett függvényt úgy kapjuk, hogy minden 'x'-ből az f(x)-nek megfelelő nyilat követve eljutunk az y=f(x) pontig, majd az 'y'-ból a g(y)-nak megfelelő nyilat követve visszajutunk az 'x' pontig) |
| g(f(x))=(f(x)−2)/3 | mivel g(x)=(x−2)/3, az x↔f(x) helyettesítést elvégezve g(f(x))=(f(x)−2)/3 adódik |
|
g(f(x))= (f(x)−2)/3= [(3*x−2)+2)]/3= (3*x−2+2)/3= (3*x)/3= x | mivel a levezetés eredményeként g(f(x))=x adódott, megállapíthatjuk, hogy a g(x) függvény valóban az f(x) függvény inverz függvénye |
Egy másik lehetőség az inverz függvény meghatározására az
f(f−1(x))=x
azonosság felhasználása. Tekintsük most is az f(x)=3*x+2 függvényt. Ekkor
f(f−1(x)) = 3*f−1(x)+2=x
amiből egyszerű átrendezéssel
f−1(x) = (x−2)/3
adódik.
Oldjuk meg az alábbi feladatokat! (vö. Veressné 1996: 26-28,31-32)
(1) Ábrázoljuk az AΧB direkt szorzat elemeit a megadott halmazok esetében!
(1.1) A = {1,2}; B = {a,b,c}
(1.2) A = {piros,zöld,kék}; B = {alma,szilva}
(1.3) A = {a,b}; B = {a,b}
(1.4) A = {1,2,3}; B = {x,y}
(2) Döntse el, hogy az alábbi halmazok direkt szorzatok vagy relációk? Adja meg azt a legszűkebb AΧB direkt szorzatot, amelynek a megadott halmazok részhalmazai!
(2.1) {(1,2), (2,1)}
(2.2) {(1,a), (2,a), (1,b), (2,b)}
(2.3) {(alma,édes), (körte,édes), (dinnye,édes), (citrom,édes)}
(2.4) {(1,1), (1,2), (1,3), (2,1), (2,2), (3,1)}
(3) Határozza meg, hogy a derékszögű koordináta-rendszerben az ℝΧℝ sík melyik részhalmazát jelölik ki a sík megadott ρ részhalmazai!
(3.1) ρ=[0;1]Χ[0;1]
(3.2) ρ={0}Χ(0;+∞)
(3.3) ρ=ℕΧ[1;+∞)
(3.4) ρ={(x,f(x)) | x∈ℝ, f(x)=x2}
(3.5) ρ={(x,y) | x,y∈ℝ, x≥0, y≤x}
(4) Bizonyítsa be, hogy a direkt szorzat az unióképzésre disztributív, azaz tetszőleges A, B és C halmazokra
AΧ(B∪C) =
(AΧB)∪(AΧC)
teljesül!
(5) Legyen A={3,4,5} és B={6,8,1,12}. Adja meg és ábrázolja a megadott kétváltozós relációkat és inverzüket!
(5.1) ρ={(a,b) | a∈A, b∈B, a<b} (ρ(a,b) ⇋ "a kisebb, mint b")
(5.2) σ={(a,b) | a∈A, b∈B, a|b} (σ(a,b) ⇋ "a osztója b-nek")
(5.3) φ={(a,b) | a∈A, b∈B, a≡b (mod 3)} (φ(a,b) ⇋ "a kongruens b-vel modulo 3, azaz a és b 3-mal osztva ugyanazt a maradékot adja, 3-nak ugyanabba a maradékosztályába tartozik")
(5.4) ψ={(a,b) | a∈A, b∈B, |a−b|≡0 (mod 2)} (ψ(a,b) ⇋ "a és b különbségének abszolút értéke páros")
(6) A megadott binér relációkra egészítse ki az alábbi táblázatokat! (Az előző feladat (5.2) pontjában szereplő σ oszthatósági relációt segítségképpen beírtuk a táblázatokba.)
| reláció tulajdonsága | igaz | hamis |
|---|---|---|
| reflexív | σ | |
| irreflexív | σ | |
| szimmetrikus | σ | |
| antiszimmetrikus | σ | |
| aszimmetrikus | σ | |
| trichotóm | σ | |
| tranzitív | σ |
| reláció nevezetessége | igaz | hamis | |
|---|---|---|---|
| ekvivalenciareláció | σ | ||
| reflexív rendezési reláció | teljes | σ | |
| parciális | σ | ||
| irreflexív rendezési reláció | teljes | σ | |
| parciális | σ | ||
(6.1)
A={"alma","bab","ceruza","fa","kréta"}
α={(x,y) | x,y∈A, "x és y azonos hosszúságú"}
(megjegyzés: egy karakterlánc hosszúsága az idézőjelek között levő karakterek száma)
(6.2)
A={"alma","bab","ceruza","fa","kréta"}
β={(x,y) | x,y∈A, "x rövidebb, mint y"}
(6.3)
A={"alma","banán","citrom","dinnye","eper"}
γ={(x,y) | x,y∈A, "x nem hosszabb, mint y"}
(6.4)
A={"alma","banán","citrom","dinnye","eper"}
δ={(x,y) | x,y∈A, "x hosszabb, mint y"}
(6.5)
az (5.1) feladatban szereplő ρ reláció az A∪B halmazon értelmezve, azaz a
ρ⊆(A∪B)Χ(A∪B) binér reláció
(6.6)
az (5.3) feladatban szereplő φ reláció az A∪B halmazon értelmezve, azaz a
φ⊆(A∪B)Χ(A∪B) binér reláció
(6.7)
az (5.4) feladatban szereplő ψ reláció az A∪B halmazon értelmezve, azaz a
ψ⊆(A∪B)Χ(A∪B) binér reláció
(7) Döntsük el, hogy a megadott relációk (megfeleltetések) közül melyek hozzárendelések, és ezek közül melyek függvények (leképezések)! A függvények közül válassza ki a szürjektív és az injektív függvényeket!
(7.1) A={3,9,49,55}, ς={(x,y) | x,y∈A, y|x, 1<y<x}
(7.1.1) A={3,9,49,55}, ς1={(x,y) | x,y∈A, y|x, 1<y≤x}
(7.1.2) A={4,9,49,55}, ς2={(x,y) | x,y∈A, y|x, 1<y<x}
(7.1.3) A={4,9,49,121}, ς3={(x,y) | x,y∈A, y|x, 1<y≤x}
(7.2) A={3,5,7}, B={12,15,49,50,71}, σ={(x,y) | x∈A, y∈B, x|y}
(7.3) A={−1,0,1,2}, B={−1,0,3}, τ={(x,y) | x∈A, y∈B, y=x2−1}
(7.4) A={−1,0,1,2}, B={−1,0,3}, ω={(x,y) | x∈A, y∈B, y=1/x}
(7.5) A={8,12,14,15}, ξ={(x,y) | x∈A, y∈ℕ, y ⇋ "x osztóinak száma"}
(7.5.1) A={8,12,14,15}, ξ1={(x,y) | x∈A, y∈ℕ, y ⇋ "x valódi (nem triviális) osztóinak száma"}
(7.5.2) A={2,4,8,16}, ξ2={(x,y) | x∈A, y∈ℕ, y ⇋ "x valódi (nem triviális) osztóinak száma"}
(7.5.3) A={2,4,8,16}, ξ3={(x,y) | x∈A, y∈{0,1,2,3}, y ⇋ "x valódi (nem triviális) osztóinak száma"}
(7.6) A={325,472,538,941}, B={2,3,4,7}, κ={(x,y) | x∈A, y∈B, y ⇋ "x tízes helyiértéken álló számjegye"}
(7.7) μ={(x,y) | x,y∈ℝ, y=x2}
(7.8) ν={(x,y) | x,y∈ℝ, y2=x}
(7.8.1) ν1={(x,y) | x∈ℝ+, y∈ℝ, y2=x}
(7.8.2) ν2={(x,y) | x,y∈ℝ+, y2=x}
(8) Határozza meg, hogy az alábbi valós függvények közül melyek injektívek, melyek szürjektívek, és melyek bijektívek!
Azoknál a függvényeknél, amelyek nem bijektívek, adja meg az értelmezési tartománynak és az értékkészletnek azokat a részhalmazait, amelyre leszűkítve a függvényeket már bijektívek lesznek!
(8.1) f(x)=|x| (abszolút érték függvény)
(8.2) f(x)=x (lineáris függvény, m=1, c=0)
(8.2.1) f(x)=2*x−4 (lineáris függvény, m=2, c=−4)
(8.3) f(x)=x2 (hatványfüggvény, n=2)
(8.4) f(x)=x3 (hatványfüggvény, n=3)
(8.5) f(x)=−2*x2+2*x (racionális egészfüggvény vagy polinom, n=2, a=−2, b=2, c=0)
(8.5.1) f(x)=x2−4*x+3 (racionális egészfüggvény vagy polinom, n=2, a=1, b=−4, c=3)
(9) Legyenek f(x) és g(x) valós függvények. Határozza meg a megadott függvények h(x)=(g∘f)(x) összetett függvényét!
(9.1) f(x)=2*x; g(x)=x−4
(9.2) f(x)=x−1; g(x)=x2−2*x
(9.3) f(x)=x−1; g(x)=−2*x2−2*x
(9.4) f(x)=x2−1; g(x)=x2+2*x
(10) Legyen f(x) valós függvény. Határozza meg a megadott függvények inverz függvényét!
(10.1) f(x)=x
(10.2) f(x)=10*x
(10.3) f(x)=x/3−2
(10.4)
| f(x) = | { | 3*x−n | ha x∈[2*n,2*n+1) (n∈ℤ) |
| 2*x+(n+1) | ha x∈[2*n+1,2*(n+1)) (n∈ℤ) |
(megjegyzés: a (10.4) feladatban szereplő f(x) függvény és a meghatározandó f−1(x) inverz függvény grafikonja itt látható)